河南省洛阳市偃师市2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 方程x﹣2=2﹣x的解是（　　）

A、x=1 B、x=﹣1 C、x=2 D、x=0

查看试题解析
2. 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A、赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
3. 若a＜b，则下列结论不一定成立的是（）

A、 $a - 1 < b - 1$ B、 $2 a < 2 b$ C、 $- \frac{a}{3} > - \frac{b}{3}$ D、 $a^{2} < b^{2}$

查看试题解析
4. 在 $△ A B C$ 中， $∠ A + ∠ B = ∠ C$ ，则 $△ A B C$ 的形状是（）

A、等腰三角形 B、钝角三角形 C、直角三角形 D、锐角三角形

查看试题解析
5. 在等式 $y = k x + b$ 中，当 $x = 2$ 时， $y = - 4$ ；当 $x = - 2$ 时， $y = 12$ ，则这个等式是（）

A、 $y = - 4 x - 4$ B、 $y = 4 x + 4$ C、 $y = - 4 x + 4$ D、 $y = 4 x - 4$

查看试题解析
6. 我国明代数学读本《算法统宗》一书有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托如果1托为5尺，那么索长和竿子长分别为多少尺？设索长为x尺，竿子长为y尺，可列方程组为（）

A、 ${\begin{array}{l} x - y = 5 \\ 2 x - y = 5 \end{array}$ B、 ${\begin{array}{l} x - y = 5 \\ y - \frac{x}{2} = 5 \end{array}$ C、 ${\begin{array}{l} x - y = 5 \\ x - \frac{y}{2} = 5 \end{array}$ D、 ${\begin{array}{l} y - x = 5 \\ x - \frac{y}{2} = 5 \end{array}$

查看试题解析
7. 如图，若 $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 关于直线 $M N$ 对称， $B B^{'}$ 交 $M N$ 于点 $O$ ，则下列说法中，不一定正确的是（）

A、 $A C = A^{^{'}} C^{^{'}}$ B、 $A B ∥ B^{'} C^{'}$ C、 $A A^{'} ⊥ M N$ D、 $B O = B^{^{'}} O$

查看试题解析
8. 下列说法不正确的是（）

A、如果两个图形全等，那么它们的形状和大小一定相同； B、面积相等的两个图形是全等图形； C、图形全等，只与形状、大小有关，而与它们的位置无关； D、全等三角形的对应边相等，对应角相等；

查看试题解析
9. 已知等腰三角形一腰上的中线将它的周长分成 $6 c m$ 和 $12 c m$ 两部分，则等腰三角形的底边长为（）

A、 $2 c m$ B、 $10 c m$ C、 $6 c m$ 或 $4 c m$ D、 $2 c m$ 或 $10 c m$

查看试题解析
10. 如图，在直角三角形 $A B C$ 中， $A C = 3$ ， $B C = 4$ ， $A B = 5$ ，且 $A C$ 在直线 $l$ 上，将 $△ A B C$ 绕点 $A$ 顺时针旋转到位置①得到点 $P_{1}$ ，将位置①的三角形绕点 $P_{1}$ 顺时针旋转到位置②得到点 $P_{2}$ ， …，按此规律继续旋转，直到得到点 $P_{2022}$ 为止（ $P_{1}$ ， $P_{2}$ ， $P_{3}$ …在直线 $l$ 上）．则 $A P_{2022} =$ （）

A、674 B、8081 C、8085 D、8088

查看试题解析

二、填空题

11. 在方程 $2 x - 3 y = 4$ 中，用含 $x$ 的代数式表示 $y$ ，则 $y =$ ．

查看试题解析
12. 不等式 $2 (x - 3) \leq x - 5$ 的正整数解为．

查看试题解析
13. 如图，若△ABC≌△DEF，AF＝2，FD＝8，则FC的长度是．

查看试题解析
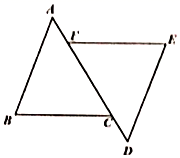14. 在一个顶点处用边长相等的三个正多边形进行密铺，其中两个是正方形和正六边形，则另一个必须是正边形．

查看试题解析
15. 如图，图1是长方形纸带，将纸带沿 $E F$ 折叠成图2，再沿 $B F$ 折叠成图3，若图3中 $∠ C F E = 108 °$ ，则图1中的 $∠ D E F$ 的度数是．

查看试题解析

三、解答题

16. 解方程（组）

(1)、 $\frac{x - 3}{2} - \frac{4 x + 1}{5} = 1$

(2)、 ${\begin{array}{l} 2 x - y = 3 \\ 3 x + 2 y = 8 \end{array}$

查看试题解析
17. 解一元一次不等式组 ${\begin{array}{l} x + 3 < 2 (x + 2) \\ \frac{x}{3} + 1 \geq \frac{3 x - 1}{4} \end{array}$ ，并把不等式组的解在数轴上表示出来.

查看试题解析
18. 一个多边形的内角和比它的外角和的3倍少180°，这个多边形的边数是多少？

查看试题解析
19. 图①、图②、图③均是6×6的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A、B、C均在格点上，只用无刻度的直尺，在给定的网格中按要求画图．

(1)、在图①中，将△ABC沿AC方向平移，当点A移动到点A₁时，画出平移后的△A₁B₁C₁；

(2)、在图②中，作△ABC关于直线MN对称的△DEF，且点D、E、F均在格点上；

(3)、在图③中，作△ABC关于点O成中心对称的△A₂B₂C₂

查看试题解析
20. 我们已经认识了图形的轴对称、平移和旋转，这是图形的三种基本变换，图形经过这样的变换，虽然位置发生了改变，但图形的形状与大小都不发生变化，反映了图形之间的全等关系．这种运用动态变换研究图形之间的关系的方法，是一种重要而且有效的方法．同学们学完了这些知识后，王老师在黑板上给大家出示了这样的一道题目：

(1)、如图，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．试说明AD＝BE；聪明的小亮很快就找到了解决该问题的方法：请你帮小亮把说理过程补充完整．
解：∵△ACB和△DCE均为等边三角形，
∴CA＝CB，CD＝CE，∠ACB＝∠DCE＝60°，（等边三角形的性质）
∴∠ACD＝  ▲  （等式的性质）
∴△ACD绕点C按逆时针方向旋转  ▲  度，能够与  ▲   重合
∴△ACD≌  ▲  （旋转变换的性质）
∴AD＝BE（   ）；

(2)、当同学们把这道题领会感悟后，王老师又在上题基础上追加了一问：试求∠AEB的度数．聪明的同学们你会解决吗？请写出你的求解过程．（此题不用写推理依据即可）．

查看试题解析
21. 如图，在四边形ABCD中，∠D＝90°，E是BC边上一点，EF⊥AE，交CD于点F.

(1)、若∠EAD＝60°，求∠DFE的度数；

(2)、若∠AEB＝∠CEF，AE平分∠BAD，试说明：∠B＝∠C.

查看试题解析
22. 某校计划购买篮球和排球两种球若干．已知：购买2个篮球，3个排球，共需花费190元；购买3个篮球的费用与购买5个排球的费用相同．

(1)、求篮球和排球的单价；

(2)、该校计划购买篮球和排球共30个．某商店有两种优惠活动（两种优惠活动不能同时参加），活动一：一律打九折；活动二：购物不超过600元时不优惠，超过600元时，超过600元的部分打八折．设购买篮球的个数为 $m$ 个，请根据以上信息，说明什么情况下选择活动二更实惠．

查看试题解析
23. 已知： $M N ∥ G H$ ，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B A C = 30 °$ ，点 $A$ 在 $M N$ 上，边 $B C$ 在 $G H$ 上，在 $R t △ D E F$ 中， $∠ D F E = 90 °$ ，边 $D E$ 在直线 $A B$ 上， $∠ E D F = 45 °$ ；

(1)、如图1，求 $∠ B A N$ 的度数；

(2)、如图2，将 $R t △ D E F$ 沿射线 $B A$ 的方向平移，当点 $F$ 在 $M N$ 上时，求 $∠ A F E$ 度数；

(3)、如图3，将 $R t △ D E F$ 沿射线 $B A$ 的方向平移到 $△ B E^{'} F^{'}$ 的位置，若点 $B$ 是 $D E$ 的中点， $D E^{'} = 6 c m$ ，则平移的距离为 $c m$ ．

(4)、将 $R t △ D E F$ 在直线 $A B$ 上平移，当以 $A$ 、 $D$ 、 $F$ 为顶点的三角形是直角三角形时，请直接写出 $∠ F A N$ 度数．

查看试题解析