广西壮族自治区贵港市覃塘区2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-08-16 类型:期末考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 经测算,火星与地球之间最大距离约为400000000千米,其中数据400000000用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 已知 , 则的值为( )A、72 B、54 C、17 D、125. 下列各式从左到右的变形,是因式分解的是( )A、 B、 C、 D、6. 七年级(1)班学生的平均年龄是12.5岁,一年后该班学生全部进入八年级(1)班就读,且全班人数保持不变,那么下列说法正确的是( )A、平均年龄不变 B、年龄的方差不变 C、年龄的众数不变 D、年龄的中位数不变7. ∠α与∠β的两边分别平行,∠α的度数是70°,则∠β的度数是( )A、 B、 C、 D、或8. 下列说法中正确的是( )A、旋转一定会改变图形的形状和大小 B、两条直线被第三条直线所截,同位角相等 C、在同一平面内,过一点有且只有一条直线与已知直线垂直 D、在同一平面内,过一点有且只有一条直线与已知直线平行9. 如图,已知两直线 与 被第三条直线 所截,下列等式一定成立的是( )
2. 经测算,火星与地球之间最大距离约为400000000千米,其中数据400000000用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 已知 , 则的值为( )A、72 B、54 C、17 D、125. 下列各式从左到右的变形,是因式分解的是( )A、 B、 C、 D、6. 七年级(1)班学生的平均年龄是12.5岁,一年后该班学生全部进入八年级(1)班就读,且全班人数保持不变,那么下列说法正确的是( )A、平均年龄不变 B、年龄的方差不变 C、年龄的众数不变 D、年龄的中位数不变7. ∠α与∠β的两边分别平行,∠α的度数是70°,则∠β的度数是( )A、 B、 C、 D、或8. 下列说法中正确的是( )A、旋转一定会改变图形的形状和大小 B、两条直线被第三条直线所截,同位角相等 C、在同一平面内,过一点有且只有一条直线与已知直线垂直 D、在同一平面内,过一点有且只有一条直线与已知直线平行9. 如图,已知两直线 与 被第三条直线 所截,下列等式一定成立的是( )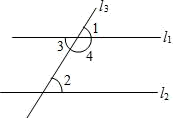 A、 B、 C、 =180° D、 =180°10. 如图,在中, , 将沿射线方向平移得到 , 再将绕点逆时针旋转得到 , 此时点恰好与点C重合,点的对应点为E,则平移的距离和旋转角的度数分别为( )
A、 B、 C、 =180° D、 =180°10. 如图,在中, , 将沿射线方向平移得到 , 再将绕点逆时针旋转得到 , 此时点恰好与点C重合,点的对应点为E,则平移的距离和旋转角的度数分别为( ) A、2, B、4, C、2, D、4,11. 如图,在中, , 点D在边上,若将沿直线折叠,使顶点A落在边上的点E处,则的周长为( )
A、2, B、4, C、2, D、4,11. 如图,在中, , 点D在边上,若将沿直线折叠,使顶点A落在边上的点E处,则的周长为( ) A、9 B、11 C、13 D、1412. 图,已知点D在上,点E,F均在上, , 平分 , 平分 , 连接 . 对于下列四个结论:①;②;③;④ , 其中正确结论的个数是( )
A、9 B、11 C、13 D、1412. 图,已知点D在上,点E,F均在上, , 平分 , 平分 , 连接 . 对于下列四个结论:①;②;③;④ , 其中正确结论的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 已知 , 若用含x的代数式表示y,则结果为 .14. 已知一组数据2,1,5,2,3,x,6只有一个众数是x,则这组数据的中位数是 .15. 如图,已知 , 则的度数为 .
 16. 若 , 则多项式的值为 .17. 如图,将绕点O逆时针旋转后得到 , 若恰好经过点A,且 , 则的度数为 .
16. 若 , 则多项式的值为 .17. 如图,将绕点O逆时针旋转后得到 , 若恰好经过点A,且 , 则的度数为 . 18. 如图,在中,于点D, , 将沿射线向右平移2个单位后得到 , 连接 , 则的面积为 .
18. 如图,在中,于点D, , 将沿射线向右平移2个单位后得到 , 连接 , 则的面积为 .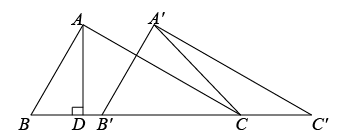
三、解答题
-
19. 因式分解:(1)、 .(2)、 .20. 如图,已知的顶点都在格点上,直线l与网线重合(每个小正方形的边长均为1个单位长度)

(1)画出关于直线l对称的;
(2)将向右平移6个单位长度,再向上平移3个单位长度,得到 , 画出;
(3)画出绕点A逆时针旋转后得到的 .21. 解方程组:(1)、(2)、22. 如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE (1)、判断OF与OD的位置关系,并进行证明.(2)、若∠AOC:∠AOD=1:5,求∠EOF的度数.23.(1)、先化简,再求值: , 其中;(2)、已知: . 求的值.24. 某中学九年级学生共进行了五次体育模拟测试,已知甲、乙同学五次测试成绩的总分相同,甲同学五次测试成绩如下统计表(尚不完整)所示:
(1)、判断OF与OD的位置关系,并进行证明.(2)、若∠AOC:∠AOD=1:5,求∠EOF的度数.23.(1)、先化简,再求值: , 其中;(2)、已知: . 求的值.24. 某中学九年级学生共进行了五次体育模拟测试,已知甲、乙同学五次测试成绩的总分相同,甲同学五次测试成绩如下统计表(尚不完整)所示:次数
第一次
第二次
第三次
第四次
第五次
成绩(分)
35
a
37
39
40
乙同学五次测试成绩的方差计算过程如下:
.
根据上述信息,完成下列问题:
(1)、a的值是;(2)、谁的体育成绩更稳定?请说明理由;(3)、如果甲同学再测试1次的成绩为38分,那么甲测试成绩的方差将发生怎样变化?为什么?25. 某农业科学研究院对A、B两种玉米进行实验种植,已知去年两种玉米分别种植10亩,B种玉米的平均亩产量比A种玉米的平均亩产量高 , 且在两种玉米的市场销售价格均为2.4元/的情况下,全部售出这两种玉米后总收入为21600元.(1)、求A,B两种玉米去年的平均亩产量;(2)、在保持种植面积不变的情况下,预计今年A,B两种玉米的平均亩产量将比去年平均亩产量分别增加和 , 且总产量将比去年总产量增加280千克,求a的值.26. 已知直线 , 动点C在与之间. (1)、如图1,若与都是锐角,求三者之间的数量关系;(2)、如图2,将一块三角尺(其中)按图中位置摆放,点D,E,F是三角尺的边与平行线的交点,若 , 求的度数;(3)、如图3,将图2中的三角尺进行适当转动,直角顶点C始终在两条平行线之间,点G在线段上,且 , 求与之间的数量关系.
(1)、如图1,若与都是锐角,求三者之间的数量关系;(2)、如图2,将一块三角尺(其中)按图中位置摆放,点D,E,F是三角尺的边与平行线的交点,若 , 求的度数;(3)、如图3,将图2中的三角尺进行适当转动,直角顶点C始终在两条平行线之间,点G在线段上,且 , 求与之间的数量关系.