甘肃省兰州市2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-08-16 类型:期末考试
一、单选题
-
1. 下列垃圾分类的图标(不含文字与字母部分)中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算中,正确的是( )A、 B、 C、 D、3. 下列判断正确的个数是( )
2. 下列运算中,正确的是( )A、 B、 C、 D、3. 下列判断正确的个数是( )
(1)能够完全重合的两个图形全等;
(2)两边和一角对应相等的两个三角形全等;
(3)两角及其夹边分别相等的两个三角形全等;
(4)全等三角形对应边相等.A、4个 B、3个 C、2个 D、1个4. 下列事件中,属于必然事件的是( )A、小明买彩票中奖 B、投掷一枚质地均匀的骰子,掷得的点数是奇数 C、等腰三角形的两个底角相等 D、 是实数,5. 等腰三角形的两边长分别为4和9,则它的周长( )A、17 B、22 C、17或22 D、216. 一个三角形三个内角的度数之比为2∶3∶7,这个三角形一定是( )A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形7. 如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数( )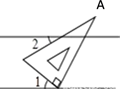 A、28° B、22° C、32° D、38°8. 如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )
A、28° B、22° C、32° D、38°8. 如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( ) A、BC=BE B、AC=DE C、∠A=∠D D、∠ACB=∠DEB9. 如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A、BC=BE B、AC=DE C、∠A=∠D D、∠ACB=∠DEB9. 如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )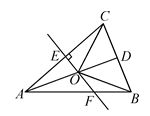 A、1对 B、2对 C、3对 D、4对10. 把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )
A、1对 B、2对 C、3对 D、4对10. 把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )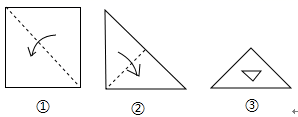 A、
A、 B、
B、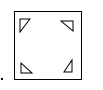 C、
C、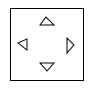 D、
D、 11. 将一副三角板按如图所示放置,则下列结论:
11. 将一副三角板按如图所示放置,则下列结论:①∠1=∠3;
②如果∠2=30°,则有AC∥DE;
③如果∠2=30°,则有BC∥AD;
④如果∠2=30°,必有∠4=∠C.其中正确的有( )
 A、①③ B、①②④ C、③④ D、①②③④12. 一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )A、
A、①③ B、①②④ C、③④ D、①②③④12. 一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 世界上最小的开花植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为 .14. 某公路急转弯处设立了一面大镜子,从镜子中看到汽车的车辆的号码如图所示,则该汽车的号码是.
 15. 一个角的补角是它的余角的4倍,则这个角是度。16. 如图,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为 度.
15. 一个角的补角是它的余角的4倍,则这个角是度。16. 如图,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为 度.
三、解答题
-
17. 计算: ;18. 先化简,再求值:
[(x+2y)2-(3x+y)(-y+3x)-5y2]÷(-4x),其中x=- ,y=2.
19. 如图,方格图中每个小正方形的边长为1,点A,B,C都是格点. (1)、画出△ABC关于直线MN对称的△A1B1C1;(2)、写出AA1的长度.20. 如图,E点为DF上的点,B为AC上的点, ∠1=∠2, ∠C=∠D.
(1)、画出△ABC关于直线MN对称的△A1B1C1;(2)、写出AA1的长度.20. 如图,E点为DF上的点,B为AC上的点, ∠1=∠2, ∠C=∠D.
试说明:AC//DF.
证明:∵ ∠1=∠2.(已知)
∠1=∠3 ,∠2=∠4( )
∴∠3=∠4( )
∴ ▲ // ▲ ( )
∴ ∠C=∠ABD( )
又 ∵ ∠C=∠D(已知)
∴∠D=∠ABD( )
∴AC//DF( )
21. 如图,点B,F,C,E在一条直线上,FB=CE,AB∥ED,AC∥FD。求证:AB=DE.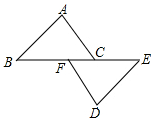 22. 中国联通在某地的资费标准为包月186元时,超出部分国内拨打0.36元/分(不足1分钟按1分钟时间收费).下表是超出部分国内拨打的收费标准:
22. 中国联通在某地的资费标准为包月186元时,超出部分国内拨打0.36元/分(不足1分钟按1分钟时间收费).下表是超出部分国内拨打的收费标准:时间/分
1
2
3
4
5
…
电话费/元
0.36
0.72
1.08
1.44
1.8
…
(1)、这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、如果用x表示超出时间,y表示超出部分的电话费,那么y与x的表达式是什么?(3)、由于业务多,小明的爸爸上月打电话已超出了包月费.如果国内拨打电话超出25分钟,他需付多少电话费?(4)、某用户某月国内拨打电话的费用超出部分是54元,那么他当月打电话超出几分钟?23. 如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2 (1)、求证:△ABC≌△ADE;(2)、找出图中与∠1、∠2相等的角(直接写出结论,不需证明).24. 如图,E,F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE,BF交于点P.
(1)、求证:△ABC≌△ADE;(2)、找出图中与∠1、∠2相等的角(直接写出结论,不需证明).24. 如图,E,F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE,BF交于点P.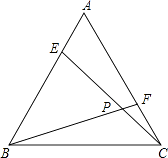 (1)、求证:CE=BF;(2)、求∠BPC的度数.25. 某商场柜台为了吸引顾客,打出了一个小广告:本专柜为了感谢广大消费者的支持和厚爱,特举行购物抽奖活动,中奖率100%,最高奖50元.具体方法是:顾客每购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准黄、红、绿、白色区域,顾客就可以分别获得50元、20元、10元、5元的购物券.(转盘的各个区域均被等分)请根据以上信息,解答下列问题:
(1)、求证:CE=BF;(2)、求∠BPC的度数.25. 某商场柜台为了吸引顾客,打出了一个小广告:本专柜为了感谢广大消费者的支持和厚爱,特举行购物抽奖活动,中奖率100%,最高奖50元.具体方法是:顾客每购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准黄、红、绿、白色区域,顾客就可以分别获得50元、20元、10元、5元的购物券.(转盘的各个区域均被等分)请根据以上信息,解答下列问题: (1)、小红的妈妈购物150元,她获得50元、5元购物券的概率分别是多少?(2)、请在转盘的适当地方写上一个区域的颜色,使得自由转动这个转盘,当它停止转动时,指针落在某一区域的事件发生概率为 , 并说出此事件.26. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
(1)、小红的妈妈购物150元,她获得50元、5元购物券的概率分别是多少?(2)、请在转盘的适当地方写上一个区域的颜色,使得自由转动这个转盘,当它停止转动时,指针落在某一区域的事件发生概率为 , 并说出此事件.26. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M. (1)、若∠ACD=124°,求∠MAB的度数;(2)、若CN⊥AM,垂足为N,试说明△CAN≌△CMN.27. 如图①,OP是∠MON的平分线,请你利用该图画一对以OP所在直线为对称轴的全等三角形.参考这个作全等三角形的方法,解答下列问题:
(1)、若∠ACD=124°,求∠MAB的度数;(2)、若CN⊥AM,垂足为N,试说明△CAN≌△CMN.27. 如图①,OP是∠MON的平分线,请你利用该图画一对以OP所在直线为对称轴的全等三角形.参考这个作全等三角形的方法,解答下列问题: (1)、如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.求∠EFA的度数;(2)、在(1)的条件下,请你判断FE与FD之间的数量关系,并说明道理.(3)、如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请问,你在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(1)、如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.求∠EFA的度数;(2)、在(1)的条件下,请你判断FE与FD之间的数量关系,并说明道理.(3)、如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请问,你在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.