浙江省历年（2018-2022年）真题分类汇编专题46 锐角三角函数
试卷更新日期：2022-08-14 类型：二轮复习
一、单选题
-
1. 如图，矩形ABCD的对角线交于点O，已知AB=m，∠BAC=∠α，则下列结论错误的是（ ）
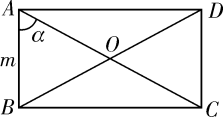A、∠BDC=∠α B、BC=m·tanα C、AO= D、BD=2. 如图是一个2×2的方阵，其中每行、每列的两数和相等，则 可以是（ ）20
a
A、 B、-1 C、0 D、3. 如图，在△ABC中，∠C=90°，设∠A，∠B，∠C所对的边分别为a，b，c，则（ ）。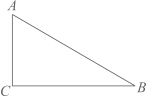
A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB4. 如图，已知菱形ABCD的边长为4，E是BC的中点，AF平分∠EAD交CD于点F，FG∥AD交AE于点G，若cosB＝ ，则FG的长是（ ）
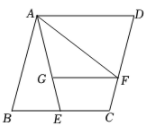A、3 B、 C、 D、5. 如图，有两张矩形纸片ABCD和EFGH、AB=EF=2cm，BC=FG=8cm，把纸片ABCD交叉叠放在纸片EFGH上，使重叠部分为平行四边形，且点D与点G重合，当两张纸片交叉所成的角最小α时，tanα等于（ ）
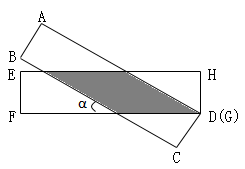A、 B、 C、 D、二、填空题
-
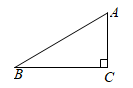
6. 如图，已知在Rt△ABC中，∠ACB=90°，AC=1，AB=2，则sinB的值是
7. sin30°=8. 图1是一个闭合时的夹子，图2是该夹子的主视示意图，夹子两边为AC，BD（点A与点B重合），点O是夹子转轴位置，OE⊥AC于点E，OF⊥BD于点F，OE=OF=1cm，AC=BD=6cm， CE=DF， CE：AE=2：3.按图示方式用手指按夹子，夹子两边绕点O转动.
(1)、当E，F两点的距离最大值时，以点A，B，C，D为顶点的四边形的周长是cm.(2)、当夹子的开口最大（点C与点D重合）时，A，B两点的距离为cm.9. 如图，已知菱形ABCD，对角线AC，BD相交于点O．若tan∠BAC= ，AC=6，则BD的长是 ．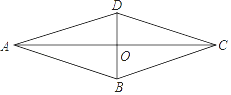
10. 如图，已知AB是⊙O的直径，BC与⊙O相切于点B，连接AC，OC，若sin∠BAC= ，则tan∠BOC=。
11. 如图， AB=10，点C在射线BQ上的动点，连结AC，作CD⊥AC， CD=AC ，动点E在AB 延长线上， tan∠QBE=3，连结 CE， DE ，当CE=DE， CE⊥DE时， BE 的长是 ．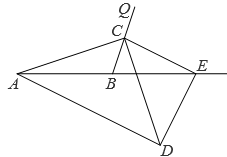
三、计算题
-
12. 计算13. 计算： .14. 计算：|-3|-2tan60°+ +( )-115. 计算：|-3|+（π-3）0- +tan45°16. 计算： ＋ －4sin45°＋ ．17. 计算： .18.(1)、计算：2﹣1+ ﹣sin30°；
（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73，sin72°≈0.95，cos72°≈0.31，tan72°≈3.08）
(2)、化简并求值：1﹣ ，其中a＝﹣ ．19. 计算：|-2|+（ ）0- +2sin30°20. 计算： .四、综合题
-
21. 如图，D是△ABC的BC边上一点，连接AD，作△ABD的外接圆，将△ADC沿直线AD折叠，点C的对应点E落在上．
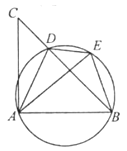(1)、求证：AE=AB．(2)、若∠CAB=90°，cos∠ADB= ，BE=2，求BC的长．22. 如图，在 中， ， 是对角线 上的两点（点 在点 左侧），且 .
(1)、求证：四边形 是平行四边形.(2)、当 ， ， 时，求 的长.23. 如图1，⊙O为锐角三角形ABC的外接圆，点D在BC上，AD交BC于点E，点F在AE上，满足∠AFB-∠BFD=∠ACB，FG∥AC交BC于点G，BE=FG，连结BD，DG．设∠ACB=α．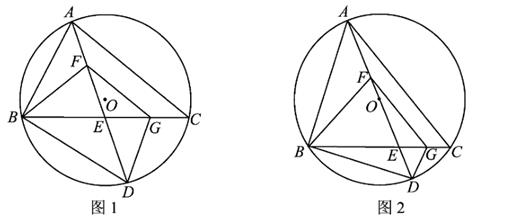
(1)、用含α的代数式表示∠BFD．(2)、求证：△BDE≌△FDG．(3)、如图2，AD为⊙O的直径．①当 的长为2时，求 的长．
②当OF：OE=4：11时，求cosα的值．
24. 如图，矩形ABCD中， ，点E是边AD的中点，点F是对角线BD上一动点， .连结EF，作点D关于直线EF的对称点P.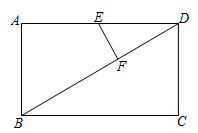
(1)、若 ，求DF的长.(2)、若 ，求DF的长.(3)、直线PE交BD于点Q，若 是锐角三角形，求DF长的取值范围.