浙江省历年(2018-2022年)真题分类汇编专题45 图形的相似(3)
试卷更新日期:2022-08-14 类型:二轮复习
一、单选题
-
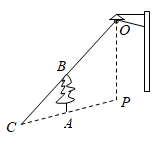
1. 如图,树AB在路灯O的照射下形成投影AC,已知路灯高 ,树影 ,树AB与路灯O的水平距离 ,则树的高度AB长是( )
 A、 B、 C、 D、2. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( )
A、 B、 C、 D、2. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( ) A、 B、 C、10 D、3. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( )
A、 B、 C、10 D、3. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( ) A、 B、1 C、 D、24. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )
A、 B、1 C、 D、24. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )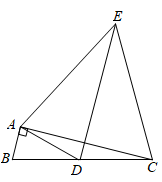 A、 B、 C、 D、25. 如图,在 中, ,以其三边为边向外作正方形,连结 ,作 于点M, 于点J, 于点K,交 于点L.若正方形 与正方形 的面积之比为5, ,则 的长为( )
A、 B、 C、 D、25. 如图,在 中, ,以其三边为边向外作正方形,连结 ,作 于点M, 于点J, 于点K,交 于点L.若正方形 与正方形 的面积之比为5, ,则 的长为( )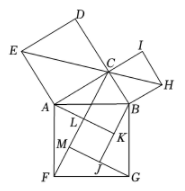 A、 B、 C、 D、6. 如图,在Rt△ABC和Rt△BDE中,∠ABC=∠BDE=90°,点A在边DE的中点上,若AB=BC,DB=DE=2,连结CE,则CE的长为( )
A、 B、 C、 D、6. 如图,在Rt△ABC和Rt△BDE中,∠ABC=∠BDE=90°,点A在边DE的中点上,若AB=BC,DB=DE=2,连结CE,则CE的长为( )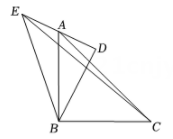 A、 B、 C、4 D、
A、 B、 C、4 D、二、填空题
-
7. 如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知 , .
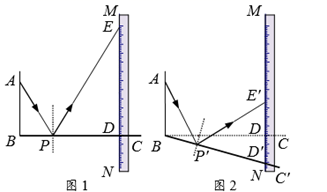 (1)、ED的长为.(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 (如图2),点P的对应点为 , 与MN的交点为D′,从A点发出的光束经平面镜 反射后,在MN上的光点为 .若 ,则 的长为.8. 如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是 .
(1)、ED的长为.(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 (如图2),点P的对应点为 , 与MN的交点为D′,从A点发出的光束经平面镜 反射后,在MN上的光点为 .若 ,则 的长为.8. 如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是 .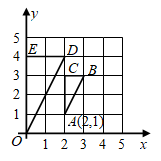 9. 如图,已知在△ABC中,D,E分别是AB,AC上的点,DE∥BC, ,若DE=2,则BC的长是 .
9. 如图,已知在△ABC中,D,E分别是AB,AC上的点,DE∥BC, ,若DE=2,则BC的长是 .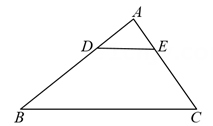 10. 如图是以点O为圆心,AB为直径的圆形纸片.点C在⊙O上,将该圆形纸片沿直线CO对折,点B落在⊙O上的点D处(不与点A重合),连接CB,CD,AD.设CD与直径AB交于点E.若AD=ED,则∠B=度; 的值等于 .
10. 如图是以点O为圆心,AB为直径的圆形纸片.点C在⊙O上,将该圆形纸片沿直线CO对折,点B落在⊙O上的点D处(不与点A重合),连接CB,CD,AD.设CD与直径AB交于点E.若AD=ED,则∠B=度; 的值等于 .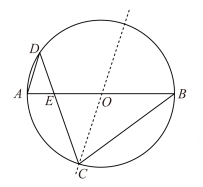 11. 某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72m,EF=2.18m.已知B,C,E,F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47m,则AB=cm.
11. 某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72m,EF=2.18m.已知B,C,E,F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47m,则AB=cm.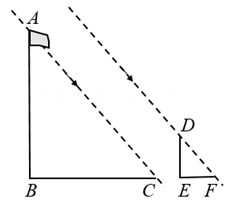 12. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.
12. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.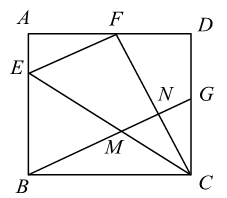 13. 如图,在菱形 ABCD中,∠A=60° ,AB=6.折叠该菱形,使点A落在边BC上的点M 处,折痕分别与边 AB,AD交于点E,F.当点M与点B重合时,EF的长为;当点M的位置变化时,DF长的最大值为 .
13. 如图,在菱形 ABCD中,∠A=60° ,AB=6.折叠该菱形,使点A落在边BC上的点M 处,折痕分别与边 AB,AD交于点E,F.当点M与点B重合时,EF的长为;当点M的位置变化时,DF长的最大值为 .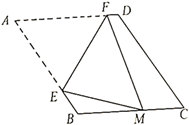
三、作图题
-
14. 如图,在6×6的方格纸中,点A,B,C均在格点上,试按要求画出相应格点图形,
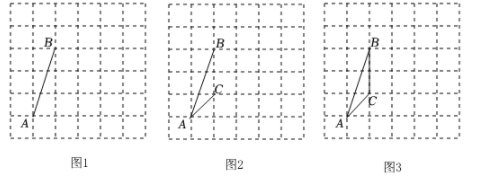 (1)、如图1,作一条线段,使它是AB向右平移一格后的图形;(2)、如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)、如图3,作一个与△ABC相似的三角形,相似比不等于1.
(1)、如图1,作一条线段,使它是AB向右平移一格后的图形;(2)、如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)、如图3,作一个与△ABC相似的三角形,相似比不等于1.四、综合题
-
15. 如图
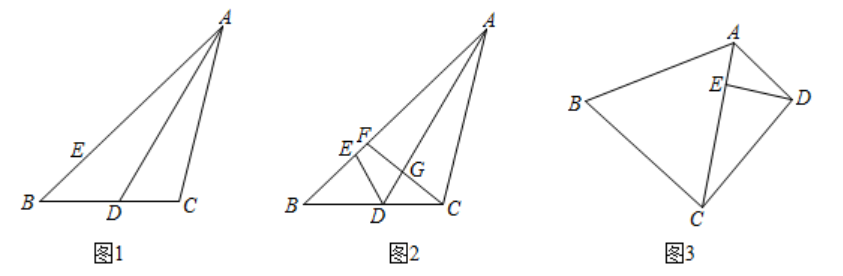 (1)、(证明体验)
(1)、(证明体验)如图1, 为 的角平分线, ,点E在 上, .求证: 平分 .
(2)、(思考探究)如图2,在(1)的条件下,F为 上一点,连结 交 于点G.若 , , ,求 的长.
(3)、(拓展延伸)如图3,在四边形 中,对角线 平分 ,点E在 上, .若 ,求 的长.
16. 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,连接DE,EF.已知四边形BFED是平行四边形, 、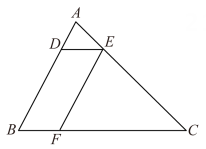 (1)、若AB=8,求线段AD的长.(2)、若△ADE的面积为1,求平行四边形BFED的面积.17. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G.
(1)、若AB=8,求线段AD的长.(2)、若△ADE的面积为1,求平行四边形BFED的面积.17. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G.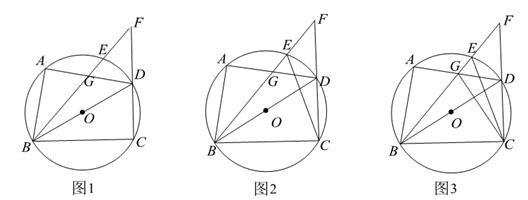 (1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .
(1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .①若 ,求 的周长.
②求 的最小值.
18. 在平面直角坐标系中,点A的坐标为 ,点B在直线 上,过点B作AB的垂线,过原点O作直线l的垂线,两垂线相交于点C.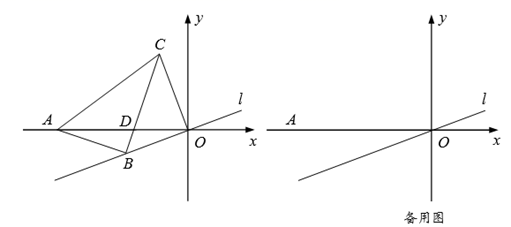 (1)、如图,点B,C分别在第三、二象限内,BC与AO相交于点D.
(1)、如图,点B,C分别在第三、二象限内,BC与AO相交于点D.①若 ,求证: .
②若 ,求四边形 的面积.
(2)、是否存在点B,使得以 为顶点的三角形与 相似?若存在,求OB的长;若不存在,请说明理由.19. 已知在平面直角坐标系xOy中,点A是反比例函数 图像上的一个动点,连结AO,AO的延长线交反比例函数 ( , )的图像于点B,过点A作AE⊥ 轴于点E。 (1)、如图1,过点B作BF⊥ 轴于点F,连结EF,
(1)、如图1,过点B作BF⊥ 轴于点F,连结EF,①若 ,求证:四边形AEFO是平行四边形;
②连结BE,若 ,求△BOE的面积。
(2)、如图2,过点E作EP∥AB,交反比例函数 ( , )的图像于点P,连结OP。试探究:对于确定的实数 ,动点A在运动过程中,△POE的面积是否会发生变化?请说明理由。
20. 小东在做九上课本123页习题:“1: 也是一个很有趣的比.已知线段AB(如图1),用直尺和圆规作AB上的一点P,使AP:AB=1: .”小东的作法是:如图2,以AB为斜边作等腰直角三角形ABC,再以点A为圆心,AC长为半径作弧,交线段AB于点P,点P即为所求作的点.小东称点P为线段AB的“趣点”.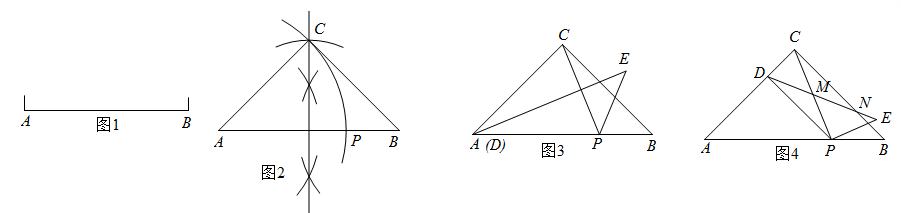 (1)、你赞同他的作法吗?请说明理由.(2)、小东在此基础上进行了如下操作和探究:连结CP,点D为线段AC上的动点,点E在AB的上方,构造△DPE,使得△DPE∽△CPB.
(1)、你赞同他的作法吗?请说明理由.(2)、小东在此基础上进行了如下操作和探究:连结CP,点D为线段AC上的动点,点E在AB的上方,构造△DPE,使得△DPE∽△CPB.①如图3,当点D运动到点A时,求∠CPE的度数.
②如图4,DE分别交CP,CB于点M,N,当点D为线段AC的“趣点”时(CD<AD),猜想:点N是否为线段ME的“趣点”?并说明理由.
21. 如图1,⊙O为锐角三角形ABC的外接圆,点D在BC上,AD交BC于点E,点F在AE上,满足∠AFB-∠BFD=∠ACB,FG∥AC交BC于点G,BE=FG,连结BD,DG.设∠ACB=α.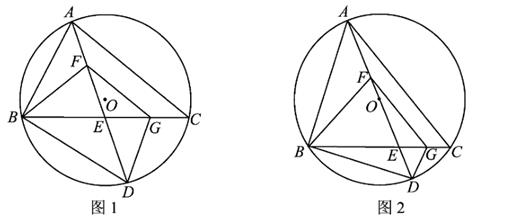 (1)、用含α的代数式表示∠BFD.(2)、求证:△BDE≌△FDG.(3)、如图2,AD为⊙O的直径.
(1)、用含α的代数式表示∠BFD.(2)、求证:△BDE≌△FDG.(3)、如图2,AD为⊙O的直径.①当 的长为2时,求 的长.
②当OF:OE=4:11时,求cosα的值.
22.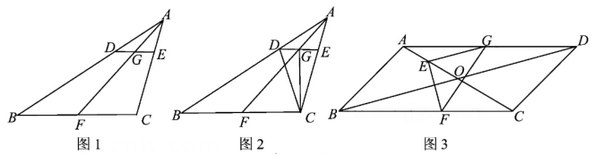 (1)、【基础巩固】
(1)、【基础巩固】
如图1,在△ABC中,D,E,F分别为AB,AC,BC上的点,DE∥BC,BF=CF,AF交DE于点G,求证:DG= EG.(2)、【尝试应用】
如图2,在(1)的条件下,连结CD,CG.若CG⊥DE,CD=6,AE=3,求 的值.(3)、【拓展提高】
如图3,在▱ABCD中,∠ADC=45°,AC与BD交于点O,E为AO上一点,EG∥BD交AD于点G,EF⊥EG交BC于点F.若∠EGF=40°,FG平分∠EFC,FG=10,求BF的长.
23. 已知在Rt△ABC中,∠ACB=90°,a,b分别表示∠A,∠B的对边,a>b.记△ABC的面积为S.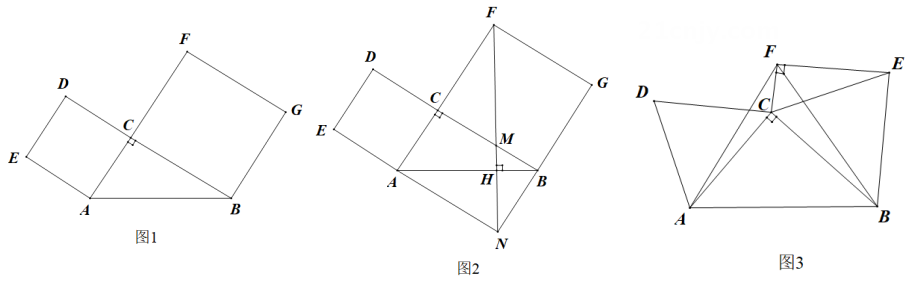 (1)、如图1,分别以AC,CB为边向形外作正方形ACDE和正方形BGFC.记正方形ACDE的面积为S1 , 正方形BGFC的面积为S2 .
(1)、如图1,分别以AC,CB为边向形外作正方形ACDE和正方形BGFC.记正方形ACDE的面积为S1 , 正方形BGFC的面积为S2 .①若S1=9,S2=16,求S的值;
②延长EA交GB的延长线于点N,连结FN,交BC于点M,交AB于点H.若FH⊥AB(如图2所示),求证:S2-S1=2S.
(2)、如图3,分别以AC,CB为边向形外作等边三角形ACD和等边三角形CBE,记等边三角形ACD的面积为S1 , 等边三角形CBE的面积为S2 . 以AB为边向上作等边三角形ABF(点C在△ABF内),连结EF,CF.若EF⊥CF,试探索S2-S1与S之间的等量关系,并说明理由.24. 如图1,已知在平面直角坐标系xOy中,四边形OABC是边长为3的正方形,其中顶点A,C分别在x轴的正半轴和y轴的正半轴上.抛物线y=-x2+bx+c经过A,C两点,与x轴交于另一个点D.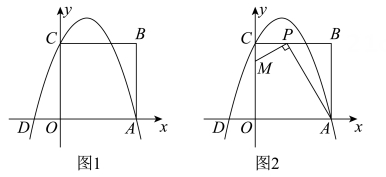 (1)、①求点A,B,C的坐标;
(1)、①求点A,B,C的坐标;②求b,c的值.
(2)、若点P是边BC上的一个动点,连结AP,过点P作PM⊥AP,交y轴于点M(如图2所示).当点P在BC上运动时,点M也随之运动.设BP=m,CM=n,试用含m的代数式表示n,并求出n的最大值.25. 如图,在矩形 ABCD中,AB=6,BC=8,动点 E从点A出发,沿边AD,DC向点C运动,A, D关于直线 BE的对称点分别为M,N,连结MN . (1)、如图,当E在边AD上且 DE=2时,求 ∠AEM的度数.(2)、当N在BC延长线上时,求DE的长,并判断直线MN与直线BD的位置关系,说明理由.(3)、当直线MN恰好经过点 C 时,求DE的长.26. 如图,在菱形ABCD中,AB=10. ,点E从点B出发沿折线B-C-D向终点D运动.过点E作点E所在的边(BC或CD)的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.
(1)、如图,当E在边AD上且 DE=2时,求 ∠AEM的度数.(2)、当N在BC延长线上时,求DE的长,并判断直线MN与直线BD的位置关系,说明理由.(3)、当直线MN恰好经过点 C 时,求DE的长.26. 如图,在菱形ABCD中,AB=10. ,点E从点B出发沿折线B-C-D向终点D运动.过点E作点E所在的边(BC或CD)的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.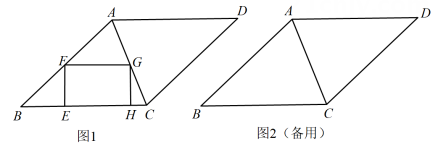 (1)、如图1,点G在AC上.求证:FA=FG.(2)、若EF=FG,当EF过AC中点时,求AG的长.(3)、已知FG=8,设点E的运动路程为s.当s满足什么条件时,以G,C,H为顶点的三角形与△BEF相似(包括全等)?27. 如图1,在正方形ABCD中,点F,H分别在边AD,AB上,连结AC,FH交于点E,已知CF=CH.
(1)、如图1,点G在AC上.求证:FA=FG.(2)、若EF=FG,当EF过AC中点时,求AG的长.(3)、已知FG=8,设点E的运动路程为s.当s满足什么条件时,以G,C,H为顶点的三角形与△BEF相似(包括全等)?27. 如图1,在正方形ABCD中,点F,H分别在边AD,AB上,连结AC,FH交于点E,已知CF=CH. (1)、线段AC与FH垂直吗?请说明理由.(2)、如图2,过点A,H,F的圆交CF于点P,连结PH交AC于点K.求证:(3)、如图3,在(2)的条件下,当点K是线段AC的中点时,求 的值.28. 如图,以AB为直径的⊙O与AH相切于点A,点C在AB左侧圆弧上,弦CD⊥AB交⊙O于点D,连结AC,AD,点A关于CD的对称点为E,直线CE交⊙O于点F,交AH于点G,
(1)、线段AC与FH垂直吗?请说明理由.(2)、如图2,过点A,H,F的圆交CF于点P,连结PH交AC于点K.求证:(3)、如图3,在(2)的条件下,当点K是线段AC的中点时,求 的值.28. 如图,以AB为直径的⊙O与AH相切于点A,点C在AB左侧圆弧上,弦CD⊥AB交⊙O于点D,连结AC,AD,点A关于CD的对称点为E,直线CE交⊙O于点F,交AH于点G, (1)、求证:∠CAG=∠AGC:(2)、当点E在AB上,连结AF交CD于点卫,若 ,求 的值;(3)、当点E在射线AB上,AB=2,以点A,C,O,F为顶点的四边形中有一组对边平行时,求AE的长.
(1)、求证:∠CAG=∠AGC:(2)、当点E在AB上,连结AF交CD于点卫,若 ,求 的值;(3)、当点E在射线AB上,AB=2,以点A,C,O,F为顶点的四边形中有一组对边平行时,求AE的长.
-