浙江省历年(2018-2022年)真题分类汇编专题45 图形的相似(2)
试卷更新日期:2022-08-14 类型:二轮复习
一、单选题
-
1. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q。若QH=2PE,PQ=15,则CR的长为( )
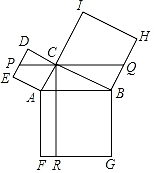 A、14 B、15 C、8 D、62. 如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2:5,且三角板的一边长为8cm,则投影三角板的对应边长为( )
A、14 B、15 C、8 D、62. 如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2:5,且三角板的一边长为8cm,则投影三角板的对应边长为( )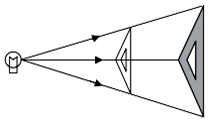 A、20cm B、10cm C、8cm D、3.2cm3. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0)。以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标为( )
A、20cm B、10cm C、8cm D、3.2cm3. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0)。以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标为( )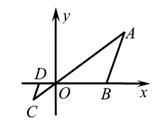 A、(-1,-1). B、( , -1) C、(-1, ) D、(-2,-1).4. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )
A、(-1,-1). B、( , -1) C、(-1, ) D、(-2,-1).4. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )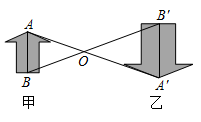 A、8 B、9 C、10 D、15
A、8 B、9 C、10 D、15二、填空题
-
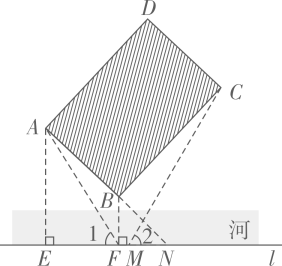
5. 如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上。在F点观测A点后,沿FN方向走到M点.观测C点发现∠1=∠2。测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为米,BC为米。
 6. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形,如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是.
6. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形,如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是.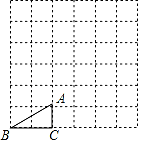 7. 如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数 (x>0)的图象经过OA的中点C,交AB于点D,连结CD.若△ACD的面积是2,则k的值是.
7. 如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数 (x>0)的图象经过OA的中点C,交AB于点D,连结CD.若△ACD的面积是2,则k的值是.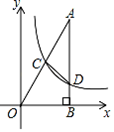 8. 如图是一张矩形纸片,点E在AB边上, 把△BCE沿直线CE对折, 使点B落在对角线AC上的点F处,连接DF。若点E,F,D在同一条直线上,AE=2,则DF= , BE=。
8. 如图是一张矩形纸片,点E在AB边上, 把△BCE沿直线CE对折, 使点B落在对角线AC上的点F处,连接DF。若点E,F,D在同一条直线上,AE=2,则DF= , BE=。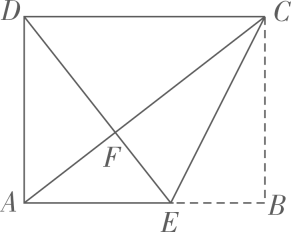 9. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 ,椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得 , , .
9. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 ,椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得 , , . (1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角 的度数达到最小值 时,A,B两点间的距离为cm(结果精确到0.1cm).(参考数据: , , )10. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=.
(1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角 的度数达到最小值 时,A,B两点间的距离为cm(结果精确到0.1cm).(参考数据: , , )10. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=. 11. 如图,经过原点O的直线与反比例函数 (a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数 (b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32,则 的值为 , 的值为.
11. 如图,经过原点O的直线与反比例函数 (a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数 (b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32,则 的值为 , 的值为.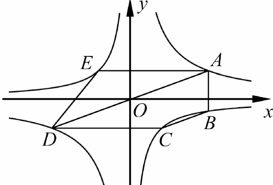
三、作图题
-
12. 如图 与 的方格都是由边长为1的小正方形组成.图1是绘成的七巧板图案,它由7个图形组成,请按以下要求选择其中一个并在图2、图3中画出相应的格点图形(顶点均在格点上).
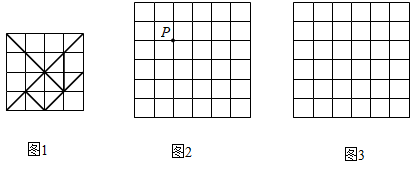 (1)、选一个四边形画在图2中,使点 为它的一个顶点,并画出将它向右平移3个单位后所得的图形.(2)、选一个合适的三角形,将它的各边长扩大到原来的 倍,画在图3中.
(1)、选一个四边形画在图2中,使点 为它的一个顶点,并画出将它向右平移3个单位后所得的图形.(2)、选一个合适的三角形,将它的各边长扩大到原来的 倍,画在图3中.四、综合题
-
13. 已知在△ABC中,AC=BC=m,D是AB边上的一点,将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A,C重合),折痕交BC边于点E.
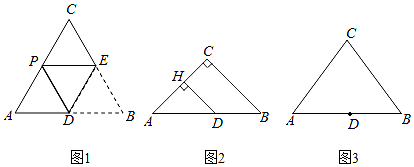 (1)、特例感知:如图1,若∠C=60°,D是AB的中点,求证:AP= AC;(2)、变式求异:如图2,若∠C=90°,m= ,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;(3)、化归探究:如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.14. 如图,在正方形ABCD中,点E在BC边上, 连接AE、∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F,设 =λ(λ>0)。
(1)、特例感知:如图1,若∠C=60°,D是AB的中点,求证:AP= AC;(2)、变式求异:如图2,若∠C=90°,m= ,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;(3)、化归探究:如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.14. 如图,在正方形ABCD中,点E在BC边上, 连接AE、∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F,设 =λ(λ>0)。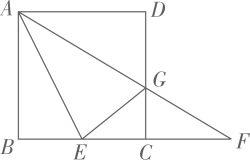 (1)、若AB=2,λ=1,求线段CF的长。(2)、连接EG,若EG⊥AF,
(1)、若AB=2,λ=1,求线段CF的长。(2)、连接EG,若EG⊥AF,①求证:点G为CD的中点。
②求λ的值。
15. 如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB。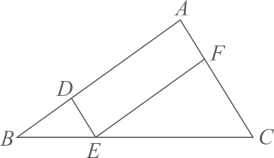 (1)、求证△BDE~△EFC。(2)、设
(1)、求证△BDE~△EFC。(2)、设①若BC=12,求线段BE的长。
②若△EFC的面积是20,求△ABC的面积。
16. 如图,在△ABC中,AB= ,∠B=45°,∠C=60°.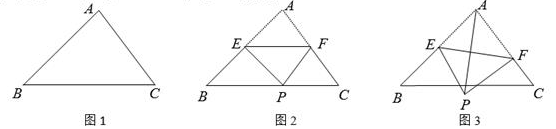 (1)、求BC边上的高线长.(2)、点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
(1)、求BC边上的高线长.(2)、点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
17. 如图1,点C是半圆O的直径AB上一动点(不包括端点), ,过点C作 交半圆于点D,连结AD,过点C作 交半圆于点E,连结EB.牛牛想探究在点C运动过程中EC与EB的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量x变化的规律.通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.
x … 0.30 0.80 1.60 2.40 3.20 4.00 4.80 5.60 … … 2.01 2.98 3.46 3.33 2.83 2.11 1.27 0.38 … … 5.60 4.95 3.95 2.96 2.06 1.24 0.57 0.10 … 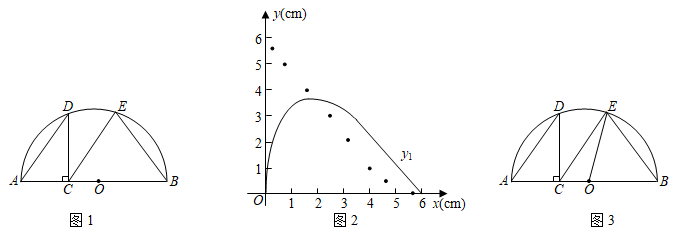 (1)、当 时, =.(2)、在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.(3)、由(2)知“AC取某值时,有 ”.如图3,牛牛连结了OE,尝试通过计算EC,EB的长来验证这一结论,请你完成计算过程.18. 如图,在 中, ,BC与 相切于点D,过点A作AC的垂线交CB的延长线于点E,交 于点F,连结BF.
(1)、当 时, =.(2)、在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.(3)、由(2)知“AC取某值时,有 ”.如图3,牛牛连结了OE,尝试通过计算EC,EB的长来验证这一结论,请你完成计算过程.18. 如图,在 中, ,BC与 相切于点D,过点A作AC的垂线交CB的延长线于点E,交 于点F,连结BF. (1)、求证:BF是 的切线.(2)、若 , ,求EF的长.19. 【性质探究】
(1)、求证:BF是 的切线.(2)、若 , ,求EF的长.19. 【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E。作DF⊥AE于点H,分别交AB,AC于点F,G。
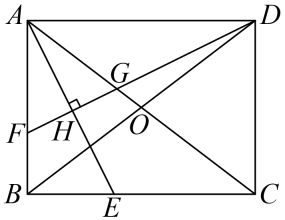 (1)、判断△AFG的形状并说明理由。(2)、求证:BF=2OG。(3)、【迁移应用】
(1)、判断△AFG的形状并说明理由。(2)、求证:BF=2OG。(3)、【迁移应用】记△DGO的面积为S1 , △DBF的面积为S2 , 当 时,求 的值。
(4)、【拓展延伸】若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF。当△BEF的面积为矩形ABCD面积的 时,请直接写出tan∠BAE的值。
20. 如图,在四边形ABCD中,∠A=∠C=90°,DE,BF分别平分∠ADC,∠ABC,并交线段AB,CD于点E,F(点E,B不重合)。在线段BF上取点M,N(点M在BN之间),使BM=2FN.当点P从点D匀速运动到点E时,点Q恰好从点M匀速运动到点N。记QN=x,PD=y,已知y=- x+12,当Q为BF中点时,y= 。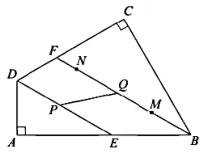 (1)、判断DE与BF的位置关系,并说明理由。(2)、求DE,BF的长。(3)、若AD=6。
(1)、判断DE与BF的位置关系,并说明理由。(2)、求DE,BF的长。(3)、若AD=6。①当DP=DF时,通过计算比较BE与BQ的大小关系。
②连结PQ,当PQ所在直线经过四边形ABCD的一个顶点时,求所有满足条件的x的值。
21. 如图1,矩形DEFG中,DG=2,DE=3,Rt△ABC中,∠ACB=90°,CA=CB=2,FG,BC的延长线相交于点O,且FG⊥BC,OG=2,OC=4。将△ABC绕点O逆时针旋转α(0°≤α<180°)得到△A'B'C'。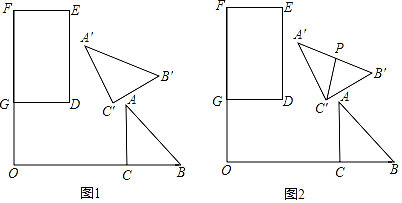 (1)、当α=30°时,求点C'到直线OF的距离。(2)、在图1中,取A'B'的中点P,连结C'P,如图2。
(1)、当α=30°时,求点C'到直线OF的距离。(2)、在图1中,取A'B'的中点P,连结C'P,如图2。①当C'P与矩形DEFG的一条边平行时,求点C'到直线DE的距离。
②当线段A'P与矩形DEFG的边有且只有一个交点时,求该交点到直线DG的距离的取值范围。
22. 在篮球比赛中,东东投出的球在点A处反弹,反弹后球运动的路线为抛物线的一部分(如图1所示建立直角坐标系),抛物线顶点为点B。 (1)、求该抛物线的函数表达式。(2)、当球运动到点C时被东东抢到,CD⊥x轴于点D,CD=2.6m。
(1)、求该抛物线的函数表达式。(2)、当球运动到点C时被东东抢到,CD⊥x轴于点D,CD=2.6m。①求OD的长。
②东东抢到球后,因遭对方防守无法投篮,他在点D处垂直起跳传球,想将球沿直线快速传给队友华华,目标为华华的接球点E(4,1.3)。东东起跳后所持球离地面高度h1(m)(传球前)与东东起跳后时间t(s)满足函数关系式h1=-2(t-0.5)²+2.7(0≤t≤1);小戴在点F(1.5,0)处拦截,他比东东晚0.3s垂直起跳,其拦截高度h2(m)与东东起跳后时间t(s)的函数关系如图2所示(其中两条抛物线的形状相同)。东东的直线传球能否越过小戴的拦截传到点E?若能,东东应在起跳后什么时间范围内传球?若不能,请说明理由(直线传球过程中球运动时间忽略不计)。
23. 如图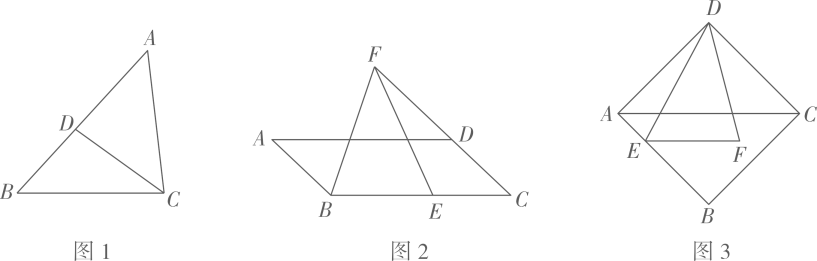 (1)、【基础巩固】
(1)、【基础巩固】如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证: .
(2)、【尝试应用】如图2,在 中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.
(3)、【拓展提高】如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF, ,AE=2,DF=5,求菱形ABCD的边长.
24. 定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.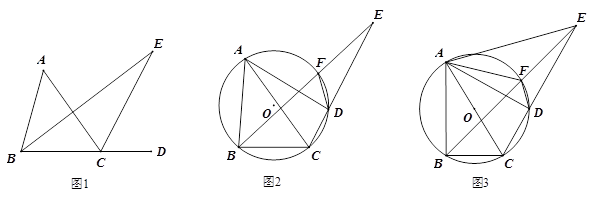 (1)、如图1,∠E是△ABC中A的遥望角,若 ,请用含a的代数式表示∠E.(2)、如图2,四边形ABCD内接于⊙O, ,四边形ABCD的外角平分线DF交⊙O于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.(3)、如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.
(1)、如图1,∠E是△ABC中A的遥望角,若 ,请用含a的代数式表示∠E.(2)、如图2,四边形ABCD内接于⊙O, ,四边形ABCD的外角平分线DF交⊙O于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.(3)、如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.①求∠AED的度数;
②若AB=8,CD=5,求△DEF的面积.
25. 如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F, 已知OB=8.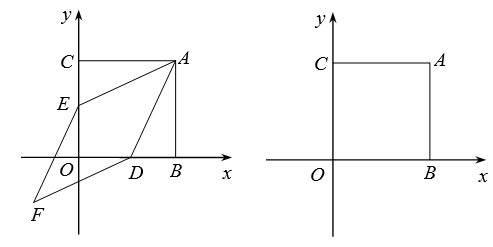 (1)、求证:四边形AEFD为菱形.(2)、求四边形AEFD的面积.(3)、若点P在x轴正半轴上(异于点D),点Q在y轴上,平面内是否存在点G,使得以点A,P, Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.26. 如图,
(1)、求证:四边形AEFD为菱形.(2)、求四边形AEFD的面积.(3)、若点P在x轴正半轴上(异于点D),点Q在y轴上,平面内是否存在点G,使得以点A,P, Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.26. 如图, (1)、【推理】
(1)、【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G. 求证: .(2)、【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若 , ,求线段DE的长.(3)、【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若 , ,求 的值(用含k的代数式表示).27. 如图,BD是半径为3的⊙O的一条弦,BD=4 ,点A是⊙O上的一个动点(不与点B,D重合),以A,B,D为顶点作▱ABCD. (1)、如图2,若点A是劣弧 的中点.
(1)、如图2,若点A是劣弧 的中点.①求证:▱ABCD是菱形;
②求▱ABCD的面积.
(2)、若点A运动到优弧 上,且▱ABCD有一边与⊙O相切.①求AB的长;
②直接写出▱ABCD对角线所夹锐角的正切值.
28. 如图,锐角三角形ABC内接于⊙O,∠BAC的平分线AG交⊙O于点G,交BC边于点F,连结BG。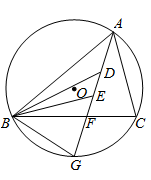 (1)、求证:△ABG∽△AFC;(2)、已知AB= ,AC=AF= ,求线段FG的长(用含 , 的代数式表示);(3)、已知点E在线段AF上(不与点A,点F重合),点D在线段AE上(不与点A,点E重合),∠ABD=∠CBE,求证: 。29. 如图,在平面直角坐标系中, 经过原点 ,分别交 轴、 轴于 , ,连结 .直线 分别交 于点 , (点 在左侧),交 轴于点 ,连结 .
(1)、求证:△ABG∽△AFC;(2)、已知AB= ,AC=AF= ,求线段FG的长(用含 , 的代数式表示);(3)、已知点E在线段AF上(不与点A,点F重合),点D在线段AE上(不与点A,点E重合),∠ABD=∠CBE,求证: 。29. 如图,在平面直角坐标系中, 经过原点 ,分别交 轴、 轴于 , ,连结 .直线 分别交 于点 , (点 在左侧),交 轴于点 ,连结 .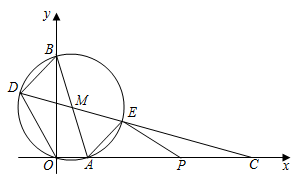 (1)、求 的半径和直线 的函数表达式.(2)、求点 , 的坐标.(3)、点 在线段 上,连结 .当 与 的一个内角相等时,求所有满足条件的 的长.
(1)、求 的半径和直线 的函数表达式.(2)、求点 , 的坐标.(3)、点 在线段 上,连结 .当 与 的一个内角相等时,求所有满足条件的 的长.
-