浙江省历年(2018-2022年)真题分类汇编专题45 图形的相似(1)
试卷更新日期:2022-08-14 类型:二轮复习
一、单选题
-
1. 学校门口的栏杆如图所示,栏杆从水平位置 绕 点旋转到 位置,已知 , ,垂足分别为 , , , , ,则栏杆 端应下降的垂直距离 为( )
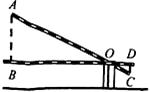 A、 B、 C、 D、2. 如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1 , S2 , ( )
A、 B、 C、 D、2. 如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1 , S2 , ( )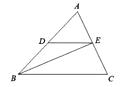 A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则3. 学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为( )
A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则3. 学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为( )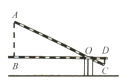 A、0.2m B、0.3m C、0.4m D、0.5m4. 如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B、C重合),连接AM交DE于点N,则( )
A、0.2m B、0.3m C、0.4m D、0.5m4. 如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B、C重合),连接AM交DE于点N,则( )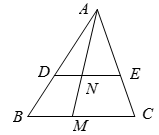 A、 B、 C、 D、5. 如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N.欧儿里得在《几何原本》中利用该图解释了 .现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1 , 图中阴影部分的面积为S2 . 若点A,L,G在同一直线上,则 的值为( )
A、 B、 C、 D、5. 如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N.欧儿里得在《几何原本》中利用该图解释了 .现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1 , 图中阴影部分的面积为S2 . 若点A,L,G在同一直线上,则 的值为( )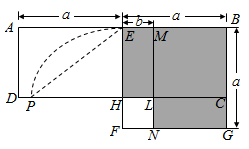 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
6. 如图,直线l1∥l2∥l3 , 直线AC交l1 , l2 , l3 , 于点A,B,C;直线DF交l1 , l2 , l3于点D,E,F,已知 ,则 =。
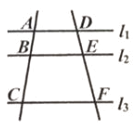 7. 三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB=∠AOE=90°,菱形的较短对角线长为2cm.若点C落在AH的延长线上,则△ABE的周长为cm.
7. 三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB=∠AOE=90°,菱形的较短对角线长为2cm.若点C落在AH的延长线上,则△ABE的周长为cm.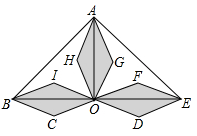 8. 如图,在平面直角坐标系中,O为坐标原点, ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F。若y= (k≠0)图象经过点C,且S△BEF=1,则k的值为 。
8. 如图,在平面直角坐标系中,O为坐标原点, ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F。若y= (k≠0)图象经过点C,且S△BEF=1,则k的值为 。 9. 如图,直线l1∥l2∥l3 , A,B,C分别为直线l1 , l2 , l3上的动点,连接AB,BC,AC,线段AC交直线l2于点D.设直线l1 , l2之间的距离为m,直线l2 , l3之间的距离为n,若∠ABC=90°,BD=4,且 则m+n的最大值为.
9. 如图,直线l1∥l2∥l3 , A,B,C分别为直线l1 , l2 , l3上的动点,连接AB,BC,AC,线段AC交直线l2于点D.设直线l1 , l2之间的距离为m,直线l2 , l3之间的距离为n,若∠ABC=90°,BD=4,且 则m+n的最大值为.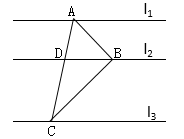 10. 如图,过原点的直线与反比例函数y= (k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为.
10. 如图,过原点的直线与反比例函数y= (k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为. 11. 如图,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的OP与△ABC的一边相切时,AP的长为.
11. 如图,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的OP与△ABC的一边相切时,AP的长为.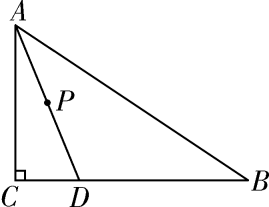 12. 如图,把某矩形纸片ABCD沿EF,GH折叠(点E,H在AD边上,点F,G在BC边上),使点B和点C落在AD边上同一点P处,A点的对称点为A'点,D点的对称点为D'点,若∠FPG=90°,△A'EP的面积为4,△D'PH的面积为1.则矩形ABCD的面积等于。
12. 如图,把某矩形纸片ABCD沿EF,GH折叠(点E,H在AD边上,点F,G在BC边上),使点B和点C落在AD边上同一点P处,A点的对称点为A'点,D点的对称点为D'点,若∠FPG=90°,△A'EP的面积为4,△D'PH的面积为1.则矩形ABCD的面积等于。
三、解答题
-
13. 如图,在正方形ABCD中,点G在边BC上(不与点B,C重合),连接AG,作DE⊥AG,于点E,BF⊥AG于点F,设 。
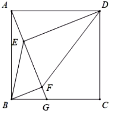 (1)、求证:AE=BF;(2)、连接BE,DF,设∠EDF= ,∠EBF= 求证:(3)、设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2 , 求 的最大值.
(1)、求证:AE=BF;(2)、连接BE,DF,设∠EDF= ,∠EBF= 求证:(3)、设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2 , 求 的最大值.四、综合题
-
14. 已知在Rt△ABC中,∠BAC=90°,AB≥AC,D,E分别为AC,BC边上的点(不包括端点),且 =m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
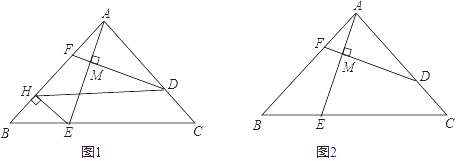 (1)、如图1,过点E作EH⊥AB于点H,连结DH.
(1)、如图1,过点E作EH⊥AB于点H,连结DH.①求证:四边形DHEC是平行四边形;
②若m= ,求证:AE=DF;
(2)、如图2,若m= ,求 的值.15. 如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=2 ,△ADC与△ABC关于AC所在的直线对称. (1)、当OB=2时,求点D的坐标;(2)、若点A和点D在同一个反比例函数的图象上,求OB的长;(3)、如图2,将第(2)题中的四边形ABCD向右平移,记平移后的四边形为A1B1C1D1 , 过点D1的反比例函数y= (k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1 , D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.16. 如图,在 中, , ,点 , 分别在 , 上,且 .
(1)、当OB=2时,求点D的坐标;(2)、若点A和点D在同一个反比例函数的图象上,求OB的长;(3)、如图2,将第(2)题中的四边形ABCD向右平移,记平移后的四边形为A1B1C1D1 , 过点D1的反比例函数y= (k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1 , D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.16. 如图,在 中, , ,点 , 分别在 , 上,且 .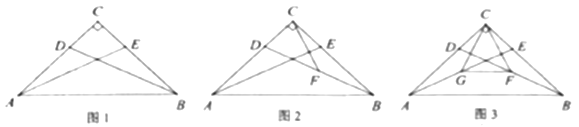 (1)、 如图1,求证: ;(2)、 如图2, 是 的中点.求证: ;(3)、 如图3, , 分别是 , 的中点.若 , ,求 的面积.17. 如图,在△ABC中,AB=AC,AD为BC边上的中线DE⊥AB于点E。
(1)、 如图1,求证: ;(2)、 如图2, 是 的中点.求证: ;(3)、 如图3, , 分别是 , 的中点.若 , ,求 的面积.17. 如图,在△ABC中,AB=AC,AD为BC边上的中线DE⊥AB于点E。 (1)、求证:△BDE∽△CAD。(2)、若AB=13,BC=10,求线段DE的长18. 已知,△ABC中,∠B=∠C,P是BC边上一点,作∠CPE=∠BPF,分别交边AC,AB于点E,F。(1)、若∠CPE=∠C(如图1),求证:PE+PF=AB。
(1)、求证:△BDE∽△CAD。(2)、若AB=13,BC=10,求线段DE的长18. 已知,△ABC中,∠B=∠C,P是BC边上一点,作∠CPE=∠BPF,分别交边AC,AB于点E,F。(1)、若∠CPE=∠C(如图1),求证:PE+PF=AB。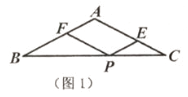 (2)、若∠CPE≠∠C,过点B作∠CBD=∠CPE,交CA(或CA的延长线)于点D.试猜想:线段PE,PF和BD之间的数量关系,并就∠CPE>∠C情形(如图2)说明理由。
(2)、若∠CPE≠∠C,过点B作∠CBD=∠CPE,交CA(或CA的延长线)于点D.试猜想:线段PE,PF和BD之间的数量关系,并就∠CPE>∠C情形(如图2)说明理由。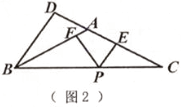 (3)、若点F与A重合(如图3),∠C=27°,且PA=AE。
(3)、若点F与A重合(如图3),∠C=27°,且PA=AE。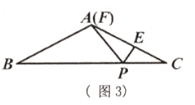
①求∠CPE的度数;
②设PB=a,PA=b,AB=c,试证明:
19. 如图,已知AB为⊙O直径,AC是⊙O的切线,连接BC交⊙O于点F,取弧BF的中点D,连接AD交BC于点E,过点E作EH⊥AB于H。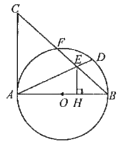 (1)、求证:△HBE∽△ABC;(2)、若CF=4,BF=5,求AC和EH的长。20. 如图,Rt△OAB的直角边OA在x轴上,顶点B的坐标为(6,8),直线CD交AB于点D(6,3),交x轴于点C(12,0)。
(1)、求证:△HBE∽△ABC;(2)、若CF=4,BF=5,求AC和EH的长。20. 如图,Rt△OAB的直角边OA在x轴上,顶点B的坐标为(6,8),直线CD交AB于点D(6,3),交x轴于点C(12,0)。 (1)、求直线CD的函数表达式;(2)、动点P在x轴上从点(-10,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t。
(1)、求直线CD的函数表达式;(2)、动点P在x轴上从点(-10,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t。①点P在运动过程中,是否存在某个位置,使得∠PDA=∠B,若存在,请求出点P的坐标;若不存在,请说明理由;
②请探索当t为何值时,在直线l上存在点M,在直线CD上存在点Q,使得以OB为一边,O,B,M,Q为顶点的四边形为菱形,并求出此时t的值。
21. 在 6×6 的方格纸中,点 A,B,C 都在格点上,按要求画图: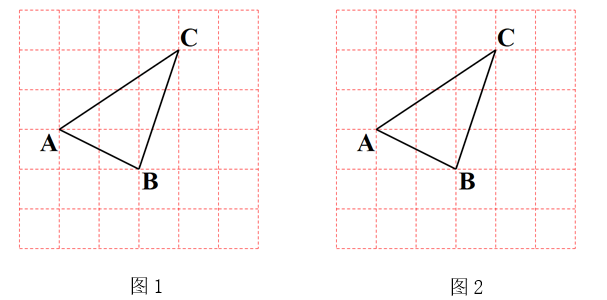 (1)、在图1中找一个格点D,使以点 A,B,C,D 为顶点的四边形是平行四边形.(2)、在图2中仅用无刻度的直尺,把线段AB 三等分(保留画图痕迹,不写画法).22. 小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1)、在图1中找一个格点D,使以点 A,B,C,D 为顶点的四边形是平行四边形.(2)、在图2中仅用无刻度的直尺,把线段AB 三等分(保留画图痕迹,不写画法).22. 小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.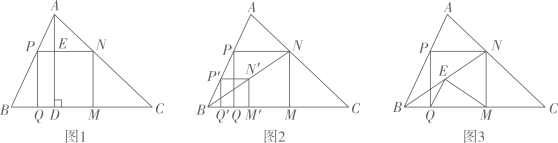
请帮助小波解决“温故”、“推理”、“拓展”中的问题.(1)、温故:如图1,在△ 中, ⊥ 于点 ,正方形 的边 在 上,顶点 , 分别在 , 上,若 , ,求正方形 的边长.(2)、操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画△ ,在 上任取一点 ,画正方形 ,使 , 在 边上, 在△ 内,连结 并延长交 于点N,画 ⊥ 于点 , ⊥ 交 于点 , ⊥ 于点 ,得到四边形P .小波把线段 称为“波利亚线”.推理:证明图2中的四边形 是正方形.
(3)、拓展:在(2)的条件下,于波利亚线 上截取 ,连结 , (如图3).当 时,猜想∠ 的度数,并尝试证明.23. 若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
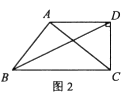 (1)、已知△ABC是比例三角形,AB=2,BC=3.请直接写出所有满足条件的AC的长;(2)、如图1,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC, ∠BAC=∠ADC.求证:△ABC是比例三角形;(3)、如图2,在(2)的条件下,当∠ADC=90°时,求 的值。24. 如图1,直线l: 与x轴交于点A(4,0),与y轴交于点B,点C是线段OA上一动点(0<AC< ),以点A为圆心,AC长为半径作⊙A交x轴于另一点D,交线段AB于点E,连结OE并延长交⊙A于点F.
(1)、已知△ABC是比例三角形,AB=2,BC=3.请直接写出所有满足条件的AC的长;(2)、如图1,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC, ∠BAC=∠ADC.求证:△ABC是比例三角形;(3)、如图2,在(2)的条件下,当∠ADC=90°时,求 的值。24. 如图1,直线l: 与x轴交于点A(4,0),与y轴交于点B,点C是线段OA上一动点(0<AC< ),以点A为圆心,AC长为半径作⊙A交x轴于另一点D,交线段AB于点E,连结OE并延长交⊙A于点F.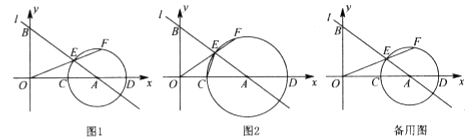 (1)、求直线l的函数表达式和tan∠BAO的值;(2)、如图2,连结CE,当CE=EF时,
(1)、求直线l的函数表达式和tan∠BAO的值;(2)、如图2,连结CE,当CE=EF时,①求证:△OCE∽△OEA;
②求点E的坐标;
(3)、当点C在线段OA上运动时,求OE·EF的最大值.25. 如图,在平面直角坐标系中,直线 分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE.动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点. (1)、求点B的坐标和OE的长;(2)、设点Q2为(m , n),当 tan∠EOF时,求点Q2的坐标;(3)、根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.①延长AD交直线BC于点Q3 , 当点Q在线段Q2Q3上时,设Q3Q=s , AP=t , 求s关于t的函数表达式.②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.26. 如图,在△ABC中,∠BAC=90°,点E在BC边上,且CA=CE,过A,C,E三点的⊙O交AB于另一点F,作直径AD,连结DE并延长交AB于点G,连结CD,CF.
(1)、求点B的坐标和OE的长;(2)、设点Q2为(m , n),当 tan∠EOF时,求点Q2的坐标;(3)、根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.①延长AD交直线BC于点Q3 , 当点Q在线段Q2Q3上时,设Q3Q=s , AP=t , 求s关于t的函数表达式.②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.26. 如图,在△ABC中,∠BAC=90°,点E在BC边上,且CA=CE,过A,C,E三点的⊙O交AB于另一点F,作直径AD,连结DE并延长交AB于点G,连结CD,CF.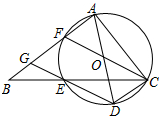 (1)、求证:四边形DCFG是平行四边形;(2)、当BE=4,CD= AB时,求⊙O的直径长.27. 如图,在等腰Rt△ABC中,∠ACB=90°,AB=14 。点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90°得到EF。
(1)、求证:四边形DCFG是平行四边形;(2)、当BE=4,CD= AB时,求⊙O的直径长.27. 如图,在等腰Rt△ABC中,∠ACB=90°,AB=14 。点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90°得到EF。 (1)、如图1,若AD=BD,点E与点C重合,AF与DC相交于点O,求证:BD=2DO.(2)、已知点G为AF的中点。
(1)、如图1,若AD=BD,点E与点C重合,AF与DC相交于点O,求证:BD=2DO.(2)、已知点G为AF的中点。①如图2,若AD=BD,CE=2,求DG的长。
②若AD=6BD,是否存在点E,使得△DEG是直角三角形?若存在,求CE的长;若不存在,试说明理由。
28. 如图,矩形ABCD中,AB=a,BC=b,点M,N分别在边AB,CD上,点E,F分别在边BC,AD上,MN,EF交于点P,记k=MN:EF.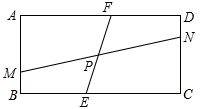 (1)、若a:b的值为1,当MN⊥EF时,求k的值。(2)、若a:b的值为 ,求k的最大值和最小值。(3)、若k的值为3,当点N是矩形的顶点,∠MPE=60°,MP=EF=3PE时,求a:b为的值。29. 如图,正方形ABCD的边长为2,E为AB的中点,P是BA延长线上的一点,连接PC交AD于点F,AP=FD
(1)、若a:b的值为1,当MN⊥EF时,求k的值。(2)、若a:b的值为 ,求k的最大值和最小值。(3)、若k的值为3,当点N是矩形的顶点,∠MPE=60°,MP=EF=3PE时,求a:b为的值。29. 如图,正方形ABCD的边长为2,E为AB的中点,P是BA延长线上的一点,连接PC交AD于点F,AP=FD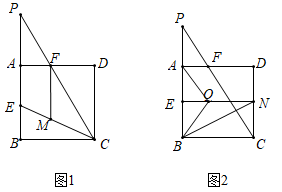 (1)、求 的值(2)、如图1,连接EC,在线段EC上取一点M,使EM=EB,连接MF,求证MF=PF;(3)、如图2,过点E作EN⊥CD于点N,在线段EN上取一点Q,使AQ=AP,连接BQ,BN.将△AQB绕点A旋转,使点Q旋转后的对应点Q'落在边AD上.请判断点B旋转后的对应点B'是否落在线段BN上,并说明理由.
(1)、求 的值(2)、如图1,连接EC,在线段EC上取一点M,使EM=EB,连接MF,求证MF=PF;(3)、如图2,过点E作EN⊥CD于点N,在线段EN上取一点Q,使AQ=AP,连接BQ,BN.将△AQB绕点A旋转,使点Q旋转后的对应点Q'落在边AD上.请判断点B旋转后的对应点B'是否落在线段BN上,并说明理由.
30. 如图,在Rt△ABC中,∠C=90°,AC=6,∠BAC=60°,AD平分∠BAC交BC于点D,过点D作DE∥AC交AB于点E,点M是线段AD上的动点,连结BM并延长分别交DE,AC于点F、G。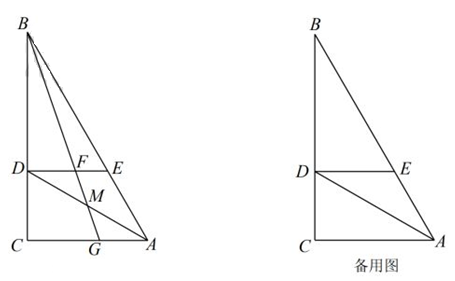 (1)、求CD的长。(2)、若点M是线段AD的中点,求 的值。(3)、请问当DM的长满足什么条件时,在线段DE上恰好只有一点P,使得∠CPG=60°?31. 小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1)、求CD的长。(2)、若点M是线段AD的中点,求 的值。(3)、请问当DM的长满足什么条件时,在线段DE上恰好只有一点P,使得∠CPG=60°?31. 小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.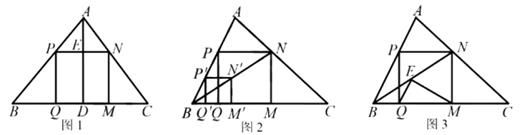
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
(1)、温故:如图1,在△ 中, ⊥ 于点 ,正方形 的边 在 上,顶点 , 分别在 , 上,若 BC=a,AD=h,求正方形 的边长(a,h表示).(2)、操作:如何能画出这个正方形PQMN呢?如图2,小波画出了图1的△ABC,然后按数学家波利亚在《怎样解题》中的方法进行操作,先在AB上任取一点 ,画正方形 ,使 , 在 边上, 在△ 内,然后连结 并延长交 于点N,画 ⊥ 于点 , ⊥ 交 于点 , ⊥ 于点 ,得到四边形P .
推理:证明图2中的四边形 是正方形.
(3)、拓展:小波把图2中的线段BN称为“波利亚线”,在该线截取 ,连结 , (如图3).当∠ =90°时,求“波利亚线”BN的长(用a、h表示).
-