浙江省历年(2018-2022年)真题分类汇编专题42 轴对称
试卷更新日期:2022-08-14 类型:二轮复习
一、单选题
-
1. 在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则( )A、m=3,n=2 B、m=-3,n=2 C、m=3,n=2 B.m=-2,n=32. 如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
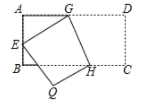 A、112° B、110° C、108° D、106°3. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
A、112° B、110° C、108° D、106°3. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )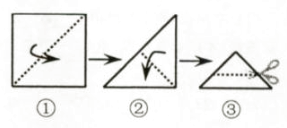 A、
A、 B、
B、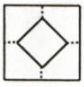 C、
C、 D、
D、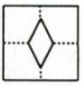 4. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )
4. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( ) A、 B、 C、 D、5. 把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )
A、 B、 C、 D、5. 把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )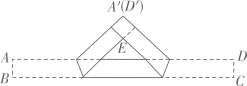 A、7+3 B、7+4 C、8+3 D、8+46. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )
A、7+3 B、7+4 C、8+3 D、8+46. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )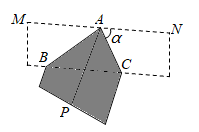 A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm27. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )
A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm27. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )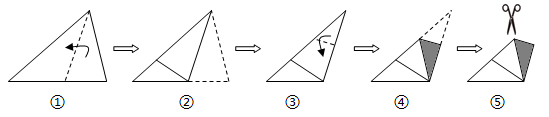 A、等腰三角形 B、直角三角形 C、矩形 D、菱形8. 如图是战机在空中展示的轴对称队形.以飞机 B、C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(40,a),则飞机D的坐标为( )
A、等腰三角形 B、直角三角形 C、矩形 D、菱形8. 如图是战机在空中展示的轴对称队形.以飞机 B、C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(40,a),则飞机D的坐标为( ) A、 B、 C、 D、9. 如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( )
A、 B、 C、 D、9. 如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( ) A、BD=10 B、HG=2 C、EG∥FH D、GF⊥BC10. 一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为( )
A、BD=10 B、HG=2 C、EG∥FH D、GF⊥BC10. 一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为( )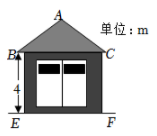 A、 B、 C、 D、11. 如图,有两张矩形纸片ABCD和EFGH、AB=EF=2cm,BC=FG=8cm,把纸片ABCD交叉叠放在纸片EFGH上,使重叠部分为平行四边形,且点D与点G重合,当两张纸片交叉所成的角最小α时,tanα等于( )
A、 B、 C、 D、11. 如图,有两张矩形纸片ABCD和EFGH、AB=EF=2cm,BC=FG=8cm,把纸片ABCD交叉叠放在纸片EFGH上,使重叠部分为平行四边形,且点D与点G重合,当两张纸片交叉所成的角最小α时,tanα等于( )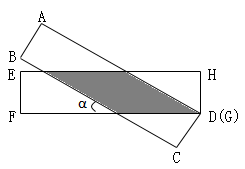 A、 B、 C、 D、12. 将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中FM,GN是折痕,若正方形EFGH与五边形MCNGF的面积相等,则 的值是( )
A、 B、 C、 D、12. 将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中FM,GN是折痕,若正方形EFGH与五边形MCNGF的面积相等,则 的值是( )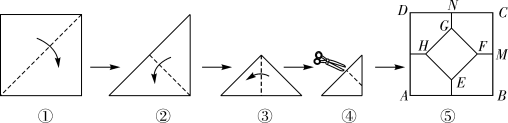 A、 B、 -1 C、 D、13. 如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A',B',A'E与BC相交于点G,B'A'的延长线过点C,若 ,则 的值为( )
A、 B、 -1 C、 D、13. 如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A',B',A'E与BC相交于点G,B'A'的延长线过点C,若 ,则 的值为( )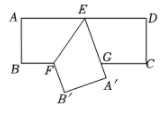 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
14. 如图,把平面内一条数轴 绕原点 逆时针旋转角 得到另一条数轴 , 轴和 轴构成一个平面斜坐标系.规定:过点 作 轴的平行线,交 轴于点 ,过点 在 轴的平行线,交 轴于点 ,若点 在 轴上对应的实数为 ,点 在 轴上对应的实数为 ,则称有序实数对 为点 的斜坐标.在某平面斜坐标系中,已知θ=60°,点 的斜坐标为 ,点 与点 关于 轴对称,则点 的斜坐标为 .
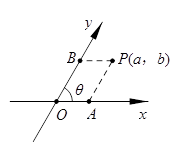 15. 折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在直线AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=。
15. 折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在直线AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=。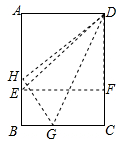 16. 如图是一张矩形纸片,点E在AB边上, 把△BCE沿直线CE对折, 使点B落在对角线AC上的点F处,连接DF。若点E,F,D在同一条直线上,AE=2,则DF= , BE=。
16. 如图是一张矩形纸片,点E在AB边上, 把△BCE沿直线CE对折, 使点B落在对角线AC上的点F处,连接DF。若点E,F,D在同一条直线上,AE=2,则DF= , BE=。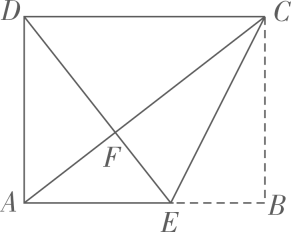 17. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连结DF,EF。若MF=AB,则∠DAF=度。
17. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连结DF,EF。若MF=AB,则∠DAF=度。 18. 如图,把某矩形纸片ABCD沿EF,GH折叠(点E,H在AD边上,点F,G在BC边上),使点B和点C落在AD边上同一点P处,A点的对称点为A'点,D点的对称点为D'点,若∠FPG=90°,△A'EP的面积为4,△D'PH的面积为1.则矩形ABCD的面积等于。
18. 如图,把某矩形纸片ABCD沿EF,GH折叠(点E,H在AD边上,点F,G在BC边上),使点B和点C落在AD边上同一点P处,A点的对称点为A'点,D点的对称点为D'点,若∠FPG=90°,△A'EP的面积为4,△D'PH的面积为1.则矩形ABCD的面积等于。 19. 如图,有一张矩形纸条ABCD,AB=5cm,BC=2cm,点M,N分别在边AB,CD上,CN=1cm。现将四边形BCNM沿MN折叠,使点B,C分别落在点B',C'上。当点B'恰好落在边CD上时,线段BM的长为cm;在点M从点A运动到点B的过程中,若边MB'与边CD交于点E,则点E相应运动的路径长为cm。
19. 如图,有一张矩形纸条ABCD,AB=5cm,BC=2cm,点M,N分别在边AB,CD上,CN=1cm。现将四边形BCNM沿MN折叠,使点B,C分别落在点B',C'上。当点B'恰好落在边CD上时,线段BM的长为cm;在点M从点A运动到点B的过程中,若边MB'与边CD交于点E,则点E相应运动的路径长为cm。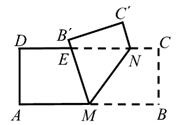 20. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.
20. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.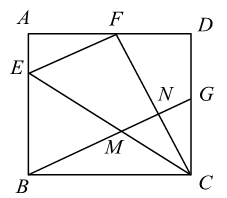 21. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动,连结CP , 点A关于直线CP的对称点为A′,连结A′C , A′P . 在运动过程中,点A′到直线AB距离的最大值是;点P到达点B时,线段A′P扫过的面积为 .
21. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动,连结CP , 点A关于直线CP的对称点为A′,连结A′C , A′P . 在运动过程中,点A′到直线AB距离的最大值是;点P到达点B时,线段A′P扫过的面积为 . 22. 如图,在菱形 ABCD中,∠A=60° ,AB=6.折叠该菱形,使点A落在边BC上的点M 处,折痕分别与边 AB,AD交于点E,F.当点M与点B重合时,EF的长为;当点M的位置变化时,DF长的最大值为 .
22. 如图,在菱形 ABCD中,∠A=60° ,AB=6.折叠该菱形,使点A落在边BC上的点M 处,折痕分别与边 AB,AD交于点E,F.当点M与点B重合时,EF的长为;当点M的位置变化时,DF长的最大值为 .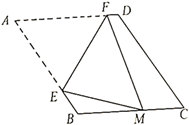 23. 如图,在扇形AOB中,点C,D在 上,将 沿弦CD折叠后恰好与OA,OB相切于点E,F。已知∠AOB=120°,OA=6,则 的度数为 ;折痕CD的长为 。
23. 如图,在扇形AOB中,点C,D在 上,将 沿弦CD折叠后恰好与OA,OB相切于点E,F。已知∠AOB=120°,OA=6,则 的度数为 ;折痕CD的长为 。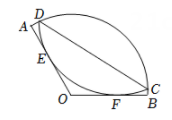
三、作图题
-
24. 图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中,按下列要求选取一个涂上阴影:
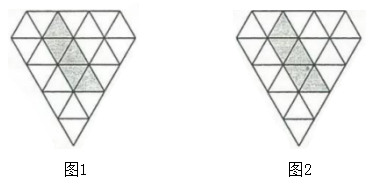 (1)、使得6个阴影小等边三角形组成一个轴对称图形。(2)、使得6个阴影小等边三角形组成一个中心对称图形。
(1)、使得6个阴影小等边三角形组成一个轴对称图形。(2)、使得6个阴影小等边三角形组成一个中心对称图形。(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
25. 图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影: (1)、使得4个阴影小等边三角形组成一个轴对称图形.(2)、使得4个阴影小等边三角形组成一个中心对称图形.
(1)、使得4个阴影小等边三角形组成一个轴对称图形.(2)、使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
26. 如图,在6×6的方格纸中,点A,B,C均在格点上,试按要求画出相应格点图形,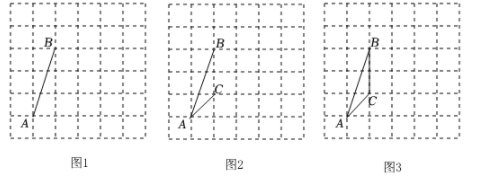 (1)、如图1,作一条线段,使它是AB向右平移一格后的图形;(2)、如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)、如图3,作一个与△ABC相似的三角形,相似比不等于1.
(1)、如图1,作一条线段,使它是AB向右平移一格后的图形;(2)、如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)、如图3,作一个与△ABC相似的三角形,相似比不等于1.四、综合题
-
27. 如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在上.
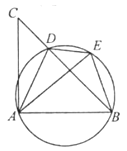 (1)、求证:AE=AB.(2)、若∠CAB=90°,cos∠ADB= ,BE=2,求BC的长.28. 已知在△ABC中,AC=BC=m,D是AB边上的一点,将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A,C重合),折痕交BC边于点E.
(1)、求证:AE=AB.(2)、若∠CAB=90°,cos∠ADB= ,BE=2,求BC的长.28. 已知在△ABC中,AC=BC=m,D是AB边上的一点,将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A,C重合),折痕交BC边于点E.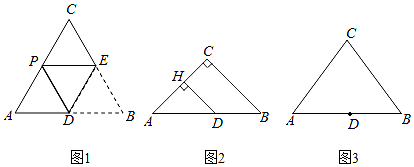 (1)、特例感知:如图1,若∠C=60°,D是AB的中点,求证:AP= AC;(2)、变式求异:如图2,若∠C=90°,m= ,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;(3)、化归探究:如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.29. 如图,在△ABC中,AB= ,∠B=45°,∠C=60°.
(1)、特例感知:如图1,若∠C=60°,D是AB的中点,求证:AP= AC;(2)、变式求异:如图2,若∠C=90°,m= ,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;(3)、化归探究:如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.29. 如图,在△ABC中,AB= ,∠B=45°,∠C=60°.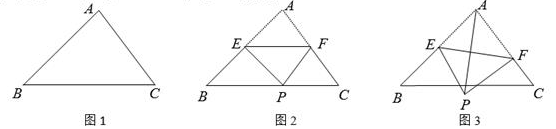 (1)、求BC边上的高线长.(2)、点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
(1)、求BC边上的高线长.(2)、点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
30. 在扇形 中,半径 ,点P在OA上,连结PB,将 沿PB折叠得到 .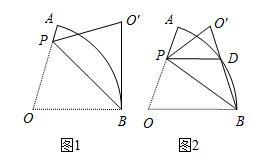 (1)、如图1,若 ,且 与 所在的圆相切于点B.
(1)、如图1,若 ,且 与 所在的圆相切于点B.①求 的度数.
②求AP的长.
(2)、如图2, 与 相交于点D,若点D为 的中点,且 ,求 的长.31. 如图,在△ABC中,∠ABC=40°, ∠ACB=90°,AE平分∠BAC交BC于点E.P是边BC上的动点(不与B,C重合),连结AP,将△APC沿AP翻折得△APD,连结DC,记∠BCD=α. (1)、如图,当P与E重合时,求α的度数.(2)、当P与E不重合时,记∠BAD=β,探究α与β的数量关系.32. 如图,将矩形纸片ABCD折叠,使点B与点D重台,点A落在点P处,折痕为EF,
(1)、如图,当P与E重合时,求α的度数.(2)、当P与E不重合时,记∠BAD=β,探究α与β的数量关系.32. 如图,将矩形纸片ABCD折叠,使点B与点D重台,点A落在点P处,折痕为EF, (1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长.33. 如图,
(1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长.33. 如图, (1)、【推理】
(1)、【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G. 求证: .(2)、【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若 , ,求线段DE的长.(3)、【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若 , ,求 的值(用含k的代数式表示).34. 如图,矩形ABCD中, ,点E是边AD的中点,点F是对角线BD上一动点, .连结EF,作点D关于直线EF的对称点P.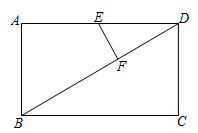 (1)、若 ,求DF的长.(2)、若 ,求DF的长.(3)、直线PE交BD于点Q,若 是锐角三角形,求DF长的取值范围.
(1)、若 ,求DF的长.(2)、若 ,求DF的长.(3)、直线PE交BD于点Q,若 是锐角三角形,求DF长的取值范围.