浙江省历年(2018-2022年)真题分类汇编专题39 弧长、扇形面积、圆锥的计算
试卷更新日期:2022-08-14 类型:二轮复习
一、单选题
-
1. 若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )A、 B、 C、 D、2. 已知圆锥的底面半径为4cm,母线长为6cm,则圆锥的侧面积为( )A、36πcm2 B、24πcm2 C、16πcm2 D、12πcm23. 某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m,高为2 m,则改建后门洞的圆弧长是( )
 A、 m B、 m C、 m D、( +2)m4. 已知扇形的半径为6,圆心角为 .则它的面积是( )A、 B、 C、 D、5. 如图,已知在矩形ABCD中,AB=1,BC= ,点P是AD边上的一个动点,连结BP,点C关于直线BP的对称点为C1 , 当点P运动时,点C1页随之运动。若点P从点A运动到点D,则线段CC1扫过的区域面积是
A、 m B、 m C、 m D、( +2)m4. 已知扇形的半径为6,圆心角为 .则它的面积是( )A、 B、 C、 D、5. 如图,已知在矩形ABCD中,AB=1,BC= ,点P是AD边上的一个动点,连结BP,点C关于直线BP的对称点为C1 , 当点P运动时,点C1页随之运动。若点P从点A运动到点D,则线段CC1扫过的区域面积是 A、π B、 C、 D、6. 如图物体由两个圆锥组成,其主视图中,∠A=90°,∠ABC=105°,若上面圆锥的侧面积为1,则下面圆锥的侧面积为( )
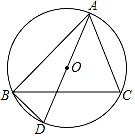
A、π B、 C、 D、6. 如图物体由两个圆锥组成,其主视图中,∠A=90°,∠ABC=105°,若上面圆锥的侧面积为1,则下面圆锥的侧面积为( ) A、2 B、 C、 D、7. 如图,△ABC内接于⊙O,∠B=65°,∠C=70°,若BC=2 ,则 的长为( )
A、2 B、 C、 D、7. 如图,△ABC内接于⊙O,∠B=65°,∠C=70°,若BC=2 ,则 的长为( )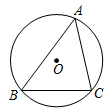 A、π B、 π C、2π D、 π8. 如图所示,矩形纸片ABCD中,AD=6cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )
A、π B、 π C、2π D、 π8. 如图所示,矩形纸片ABCD中,AD=6cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )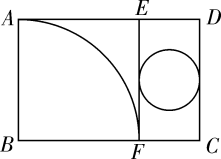 A、3.5cm B、4cm C、4.5cm D、5cm9. 已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是( )A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm210. 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,以点B为圆心,BC长为半径画弧,交边AB于点D,则 的长为( )
A、3.5cm B、4cm C、4.5cm D、5cm9. 已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是( )A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm210. 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,以点B为圆心,BC长为半径画弧,交边AB于点D,则 的长为( ) A、 B、 C、 D、11. 如图,AB是圆锥的母线,BC为底面直径,已知BC=6cm,圆锥的面积为15πcm2 , 则sin∠ABC的值为( )
A、 B、 C、 D、11. 如图,AB是圆锥的母线,BC为底面直径,已知BC=6cm,圆锥的面积为15πcm2 , 则sin∠ABC的值为( )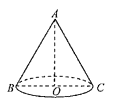 A、 B、 C、 D、12. 如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N.欧儿里得在《几何原本》中利用该图解释了 .现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1 , 图中阴影部分的面积为S2 . 若点A,L,G在同一直线上,则 的值为( )
A、 B、 C、 D、12. 如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N.欧儿里得在《几何原本》中利用该图解释了 .现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1 , 图中阴影部分的面积为S2 . 若点A,L,G在同一直线上,则 的值为( )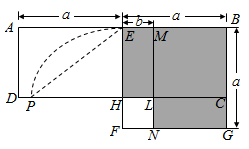 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知扇形的弧长为2 ,圆心角为60°,则它的半径为 .14. 若扇形的圆心角为 120° ,半径为 ,则它的弧长为 .15. 如图,将线段AB绕点A顺时针旋转30°,得到线段AC.若AB=12,则点B经过的路径 长度为 .(结果保留π)
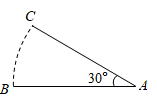 16. 若扇形的圆心角为 ,半径为17,则扇形的弧长为.17. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图, 分别与 相切于点C,D,延长 交于点P.若 , 的半径为 ,则图中 的长为 .(结果保留 )
16. 若扇形的圆心角为 ,半径为17,则扇形的弧长为.17. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图, 分别与 相切于点C,D,延长 交于点P.若 , 的半径为 ,则图中 的长为 .(结果保留 )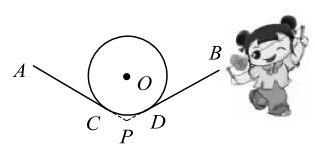 18. 若扇形的圆心角为45°,半径为3,则该扇形的弧长为。19. 如图,在半径为 的圆形纸片中,剪一个圆心角为90°的最大扇形(阴影部分),则这个扇形的面积为;若将此扇形围成一个无底的圆锥(不计接头),则圆锥底面半径为 。
18. 若扇形的圆心角为45°,半径为3,则该扇形的弧长为。19. 如图,在半径为 的圆形纸片中,剪一个圆心角为90°的最大扇形(阴影部分),则这个扇形的面积为;若将此扇形围成一个无底的圆锥(不计接头),则圆锥底面半径为 。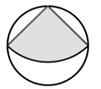 20. 如图是一个圆锥形冰淇淋外壳(不计厚度).已知其母线长为12cm,底面圆半径为3cm,则这个冰淇淋外壳的侧面积等于cm2(结果精确到个位).
20. 如图是一个圆锥形冰淇淋外壳(不计厚度).已知其母线长为12cm,底面圆半径为3cm,则这个冰淇淋外壳的侧面积等于cm2(结果精确到个位). 21. 如图,公园内有一个半径为20米的圆形草坪, , 是圆上的点, 为圆心, ,从 到 只有路 ,一部分市民为走“捷径”,踩坏了花草,走出了一条小路 .通过计算可知,这些市民其实仅仅少走了步(假设1步为0.5米,结果保留整数).(参考数据: , 取3.142)
21. 如图,公园内有一个半径为20米的圆形草坪, , 是圆上的点, 为圆心, ,从 到 只有路 ,一部分市民为走“捷径”,踩坏了花草,走出了一条小路 .通过计算可知,这些市民其实仅仅少走了步(假设1步为0.5米,结果保留整数).(参考数据: , 取3.142)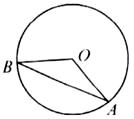 22. 如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,∠AOB=120°,从A到B只有路弧AB,一部分市民走“捷径”,踩坏了花草,走出了一条小路AB。通过计算可知,这些市民其实仅仅少走了步(假设1步为0.5米,结果保留整数)。(参考数据: ≈1.732,π取3.142)
22. 如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,∠AOB=120°,从A到B只有路弧AB,一部分市民走“捷径”,踩坏了花草,走出了一条小路AB。通过计算可知,这些市民其实仅仅少走了步(假设1步为0.5米,结果保留整数)。(参考数据: ≈1.732,π取3.142)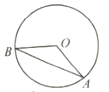 23. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动,连结CP , 点A关于直线CP的对称点为A′,连结A′C , A′P . 在运动过程中,点A′到直线AB距离的最大值是;点P到达点B时,线段A′P扫过的面积为 .
23. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动,连结CP , 点A关于直线CP的对称点为A′,连结A′C , A′P . 在运动过程中,点A′到直线AB距离的最大值是;点P到达点B时,线段A′P扫过的面积为 . 24. 如图1是小明制作的一副弓箭,点A , D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉弓的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
24. 如图1是小明制作的一副弓箭,点A , D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉弓的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.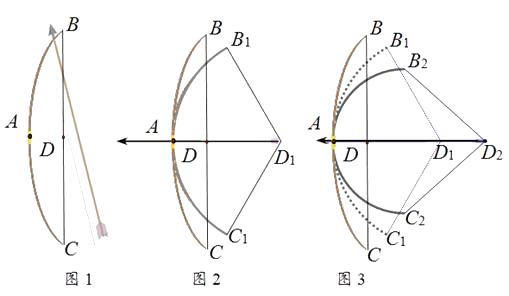 (1)、图2中,弓臂两端B1 , C1的距离为cm.(2)、如图3,将弓箭继续拉到点D2 , 使弓臂B2AC2为半圆,则D1D2的长为cm.
(1)、图2中,弓臂两端B1 , C1的距离为cm.(2)、如图3,将弓箭继续拉到点D2 , 使弓臂B2AC2为半圆,则D1D2的长为cm.三、综合题
-
25. 如图,半径为6的⊙O与Rt△ABC的边AB相切于点A,交边BC于点C,D,∠B=90°,连结OD,AD.
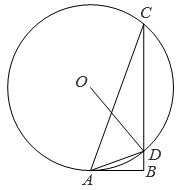 (1)、若∠ACB=20°,求 的长(结果保留π).(2)、求证:AD平分∠BDO.
(1)、若∠ACB=20°,求 的长(结果保留π).(2)、求证:AD平分∠BDO.