浙江省历年（2018-2022年）真题分类汇编专题36 圆的性质（1）
试卷更新日期：2022-08-14 类型：二轮复习
一、单选题
-
1. 尺规作图特有的魅力曾使无数人沉湎其中．传说拿破仑通过下列尺规作图考他的大臣：
①将半径为r的⊙O六等分，依次得到A，B，C，D，E，F六个分点；②分别以点A，D为圆心，AC长为半径画弧，G是两弧的一个交点；③连结OG．问：OG的长是多少？大臣给出的正确答案应是（ ）
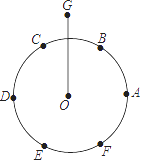A、 r B、（1+ ）r C、（1+ ）r D、 r2. 用反证法证明时，假设结论“点在圆外”不成立，那么点与圆的位置关系只能是（ ）A、点在圆内 B、点在圆上 C、点在圆心上 D、点在圆上或圆内3. 如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，则OF的长度是（ ）
A、3cm B、 cm C、2.5cm D、 cm4. 如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（ ）
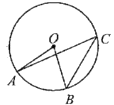A、75° B、70° C、65° D、35°5. 一块圆形宣传标志牌如图所示，点A，B，C在⊙O上，CD垂直平分AB于点D，现测得AB=8dm，DC=2dm，则圆形标志牌的半径为（ ）
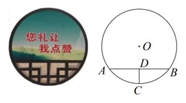A、6dm B、5dm C、4dm D、3dm6. 如图，点A，B，C，D，E均在⊙O上，∠BAC=15°，∠CED=30°，则∠BOD的度数为（ ）
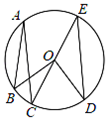A、45° B、60° C、75° D、90°7. 如图，已知四边形ABCD内接于⊙O，∠ABC＝70°，则∠ADC的度数是（ ）
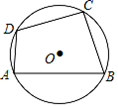A、70° B、110° C、130° D、140°8. 如图，在等腰△ABC中， AB=AC=2 ，BC=8， 按下列步骤作图：
①以点A为圆心，适当的长度为半径作弧，分别交AB，AC于点E，F，再分别以点E，F为圆心，大于 EF的长为半径作弧相交于点H，作射线AH；②分别以点A，B为圆心，大于 AB的长为半径作弧相交于点M，N，作直线MN，交射线AH于点0；③以点为圆心，线段OA长为半径作圆。则⊙O的半径为（ ）
A、2 B、10 C、4 D、59. 如图，已知BC是⊙O的直径，半径OA⊥BC，点D在劣弧AC上(不与点A，点C重合)，BD与OA交于点E，设∠AED=α，∠AOD=β，则（ ）
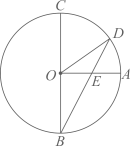A、3α+β=180° B、2α+β=180° C、3α-β=90° D、2α-β=90°二、填空题
-
10. 如图，AB是⊙的直径，点C是半径OA的中点，过点C作DE⊥AB，交O于点D，E两点，过点D作直径DF，连结AF，则∠DEA=。
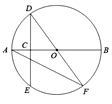11. 如图，在⊙O中，弦 ，点C在AB上移动，连结OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为 ．
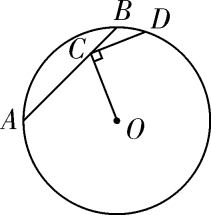12. 已知一条弧所对的圆周角的度数是15°，则它所对的圆心角的度数是.13. 如图，已知AB是半圆O的直径，弦CD∥AB，CD＝8，AB＝10，则CD与AB之间的距离是.三、综合题
-
14. 如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．
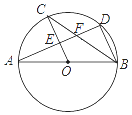(1)、求证：AE=ED；(2)、若AB=10，∠CBD=36°，求 的长．15. 如图，△ABC内接于⊙O，AB为⊙O的直径，AB=10，AC=6。连结OC，弦AD分别交OC，BC于点E，F，其中点E是AD的中点。
(1)、求证：∠CAD=∠CBA。(2)、求OE的长。16. 如图，C，D为⊙O上两点，且在直径AB两侧，连结CD交AB于点E，G是 上一点，∠ADC=∠G。
(1)、求证：∠1=∠2。(2)、点C关于DG的对称点为F，连结CF.当点F落在直径AB上时，CF=10，tan∠1= ，求⊙O的半径。17. 如图，在△ABC中，∠BAC＝90°，点E在BC边上，且CA＝CE，过A，C，E三点的⊙O交AB于另一点F，作直径AD，连结DE并延长交AB于点G，连结CD，CF．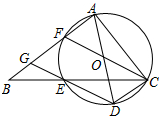
(1)、求证：四边形DCFG是平行四边形；(2)、当BE＝4，CD＝ AB时，求⊙O的直径长．18. 如图，已知锐角三角形ABC内接于⊙O，OD⊥BC于点D，连接OA.
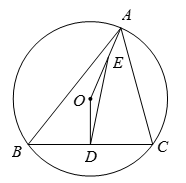(1)、若∠BAC=60°，①求证：OD= OA.
②当OA=1时，求△ABC面积的最大值。
(2)、点E在线段OA上，（OE=OD.连接DE，设∠ABC=m∠OED.∠ACB=n∠OED（m，n是正数）.若∠ABC<∠ACB，求证：m-n+2=0.