浙江省历年（2018-2022年）真题分类汇编专题35 四边形的综合
试卷更新日期：2022-08-14 类型：二轮复习
一、单选题
-
1. 如图，菱形ABCD中， ，点P从点B出发，沿折线 方向移动，移动到点D停止.在 形状的变化过程中，依次出现的特殊三角形是（ ）
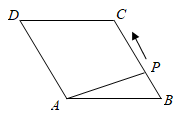A、直角三角形→等边三角形→等腰三角形→直角三角形 B、直角三角形→等腰三角形→直角三角形→等边三角形 C、直角三角形→等边三角形→直角三角形→等腰三角形 D、等腰三角形→等边三角形→直角三角形→等腰三角形2. 我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式．后人借助这种分割方法所得的图形证明了勾股定理，如图所示的矩形由两个这样的图形拼成，若 ， ，则该矩形的面积为（ ）
A、20 B、24 C、 D、3. 下列命题中，正确的是（ ）A、梯形的对角线相等 B、菱形的对角线不相等 C、矩形的对角线不能相互垂直 D、平行四边形的对角线可以互相垂直4. 如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG．DE，FG， 的中点分别是M，N，P，Q．若MP+NQ=14，AC+BC=18，则AB的长为（ ）
A、 B、 C、13 D、165. 如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B移动，移动到点B停止，延长EO交CD于点F，则四边形AECF形状的变化依次为（ ）
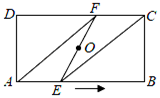A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形二、填空题
-
6. 如图，在菱形ABCD中，边长为10，∠A=60°．顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…．则四边形A2B2C2D2的周长是；四边形A2013B2013C2013D2013的周长是 ．
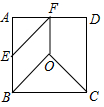
7. 把边长为2的正方形纸片ABCD分割成如图四块，其中点O为正方形的中心，点E，F分别为AB，AD的中点，用这四块纸片拼成与此正方形不全等的四边形MNPQ（要求这四块纸片不重叠无缝隙），则四边形MNPQ的周长是。
三、作图题
-
8. 如图，P，Q是方格纸中的两格点，请按要求画出以PQ为对角线的格点四边形．
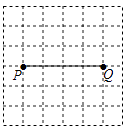(1)、在图1中画出一个面积最小的¨PAQB．(2)、在图2中画出一个四边形PCQD，使其是轴对称图形而不是中心对称图形，且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到．注：图1，图2在答题纸上．四、综合题
-
9. 如图，抛物线y=a（x﹣1）2+4与x轴交于点A，B，与y轴交于点C，过点C作CD∥x轴交抛物线的对称轴于点D，连接BD，已知点A的坐标为（﹣1，0）
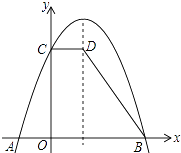(1)、求该抛物线的解析式；(2)、求梯形COBD的面积．10. 如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF的两边相交于A、B和C、D，连接OA，此时有OA∥PE．
(1)、求证：AP=AO；(2)、若tan∠OPB= ，求弦AB的长；(3)、若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为 ， 能构成等腰梯形的四个点为或或 ．11. 在正方形ABCD中，点M是边AB的中点，点E在线段AM上（不与点A重合），点F在边BC上，且AE=2BF，连接EF，以EF为边在正方形ABCD内作正方形EFGH．
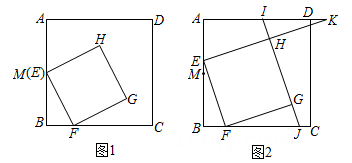(1)、如图1．若AB=4，当点E与点M重合时，求正方形EFGH的面积(2)、如图2．已知直线HG分别与边AD，BC交于点I，J，射线EH与射线AD交于点K．①求证：EK=2EH；
②设∠AEK=α，△FGJ和四边形AEHI的面积分别为S1、S2 ．
求证： =4sin2α-1．
12. 如图，在矩形 ABCD中，AB=6，BC=8，动点 E从点A出发，沿边AD，DC向点C运动，A， D关于直线 BE的对称点分别为M，N，连结MN ．
(1)、如图，当E在边AD上且 DE=2时，求 ∠AEM的度数．(2)、当N在BC延长线上时，求DE的长，并判断直线MN与直线BD的位置关系，说明理由．(3)、当直线MN恰好经过点 C 时，求DE的长．
-