浙江省历年（2018-2022年）真题分类汇编专题31 平行四边形的判定与性质

试卷更新日期：2022-08-14 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图，在△ABC中，AB＝AC＝8，点E，F，G分别在边AB，BC，AC上，EF∥AC，GF∥AB，则四边形AEFG的周长是（）

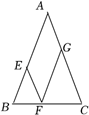A、8 B、16 C、24 D、32

查看试题解析
2. 如图，在平行四边形 $A B C D$ 中， $A D = 2 A B = 2$ ， $∠ A B C = 60 °$ ， $E$ ， $F$ 是对角线 $B D$ 上的动点，且 $B E = D F$ ， $M$ ， $N$ 分别是边 $A D$ ，边 $B C$ 上的动点．下列四种说法：
①存在无数个平行四边形 $M E N F$ ；
②存在无数个矩形 $M E N F$ ；
③存在无数个菱形 $M E N F$ ；
④存在无数个正方形 $M E N F$ ．其中正确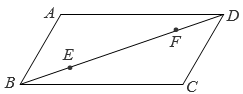的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
3. 如图，在△ABC中，AB=AC=8．点E、F、G分别在边AB、BC、AC上．EF∥AC、GF∥AB、则四边形AEFG的周长是（）

A、32 B、24 C、16 D、8

查看试题解析
4. 如图，在 $△ A B C$ 中， $A B = 4$ ， $A C = 5$ ， $B C = 6$ ，点D，E，F分别是AB，BC，CA的中点，连结DE，EF，则四边形ADEF的周长为（）

A、6 B、9 C、12 D、15

查看试题解析
5. 如图是一个由5张纸片拼成的 $▱ A B C D$ ，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为 $S_{1}$ ，另两张直角三角形纸片的面积都为 $S_{2}$ ，中间一张矩形纸片 $E F G H$ 的面积为 $S_{3}$ ， $F H$ 与 $G E$ 相交于点O.当 $△ A E O ， △ B F O ， △ C G O ， △ D H O$ 的面积相等时，下列结论一定成立的是（）

A、 $S_{1} = S_{2}$ B、 $S_{1} = S_{3}$ C、 $A B = A D$ D、 $E H = G H$

查看试题解析
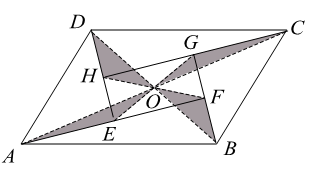6. 如图，在△ABC中，∠A=40°，AB=AC，点D在AC边上，以CB，CD为边作 $▱$ BCDE，则∠E的度数为（）

A、40° B、50° C、60° D、70°

查看试题解析
7. 如图，在 $▱ A B C D$ 中， $A B = 2$ ， $B C = 3$ .以点 $C$ 为圆心，适当长为半径画弧，交 $B C$ 于点 $P$ ，交 $C D$ 于点 $Q$ ，再分别以点 $P$ ， $Q$ 为圆心，大于 $\frac{1}{2} P Q$ 的长为半径画弧，两弧相交于点 $N$ ，射线 $C N$ 交 $B A$ 的延长线于点 $E$ ，则 $A E$ 的长是（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{6}{5}$ D、 $\frac{3}{2}$

查看试题解析
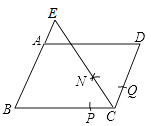8. 如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连结OE．若∠ABC=60°，∠BAC=80°，则∠1的度数为（）

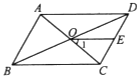A、50° B、40° C、30° D、20°

查看试题解析

二、填空题

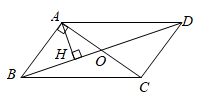
9. 如图，在▱ABCD中，对角线AC ， BD交于点O ， AB⊥AC ， AH⊥BD于点H ，若AB＝2，BC＝2 $\sqrt{3}$ ，则AH的长为．

查看试题解析
10. 如图，平移图形M，与图形N可以拼成一个平行四边形，则图中α的度数是°.

查看试题解析

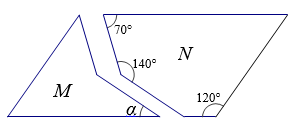
三、作图题

11. 如图，在5×5的网格中，△ABC的一个顶点都在格点上。

(1)、在图1中画出一个以AB为边的 $▱$ ABDE，使顶点D，E在格点上。

(2)、在图2中画出一条恰好平分△ABC周长的直线l（至少经过两个格点）。

查看试题解析

四、解答题

12. 如图，在▱ABCD中，AC是对角线，BE⊥AC，DF⊥AC，垂足分别为点E，F。
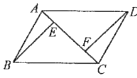
求证：AE＝CF。

查看试题解析

五、综合题

13. 如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，连接DE，EF．已知四边形BFED是平行四边形， $\frac{D E}{B C} = \frac{1}{4}$ 、

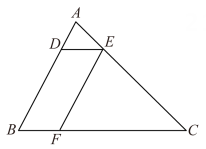(1)、若AB=8，求线段AD的长．

(2)、若△ADE的面积为1，求平行四边形BFED的面积．

查看试题解析
14. 如图，在△ABC 中， AD⊥BC于点D、E、F分别是AC、AB 的中点，O是 DF 的中点， EO 的延长线交线段 BD 于点G，连结 DE、EF、FG．

(1)、求证：四边形 DEFG 是平行四边形．

(2)、当AD=5，tan∠EDC= $\frac{5}{2}$ =时，求 FG 的长．

查看试题解析
15. 如图，在 $▱ A B C D$ 中， $E$ ， $F$ 是对角线 $B D$ 上的两点（点 $E$ 在点 $F$ 左侧），且 $∠ A E B = ∠ C F D = 90 °$ .

(1)、求证：四边形 $A E C F$ 是平行四边形.

(2)、当 $A B = 5$ ， $\tan ∠ A B E = \frac{3}{4}$ ， $∠ C B E = ∠ E A F$ 时，求 $B D$ 的长.

查看试题解析
16. 问题：如图，在 $▱ A B C D$ 中， $A B = 8$ ， $A D = 5$ ， $∠ D A B$ ， $∠ A B C$ 的平分线AE，BF分别与直线CD交于点E，F，求EF的长.

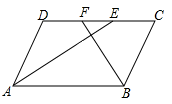
答案： $E F = 2$ .

(1)、探究：把“问题”中的条件“ $A B = 8$ ”去掉，其余条件不变.

①当点E与点F重合时，求AB的长；

②当点E与点C重合时，求EF的长.

(2)、把“问题”中的条件“ $A B = 8$ ， $A D = 5$ ”去掉，其余条件不变，当点C，D，E，F相邻两点间的距离相等时，求 $\frac{A D}{A B}$ 的值.

查看试题解析
17. 如图，点E是 $▱$ ABCD的边CD的中点，连结AE并延长，交BC的延长线于点F。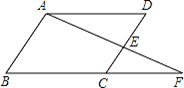

(1)、若AD的长为2，求CF的长。

(2)、若∠BAF=90°，试添加一个条件，并写出∠F的度数。

查看试题解析
18. 在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合(如图1) ，其中∠ACB=∠DFE=90°，BC=EF=3cm，AC=DF=4cm，并进行如下研究活动。

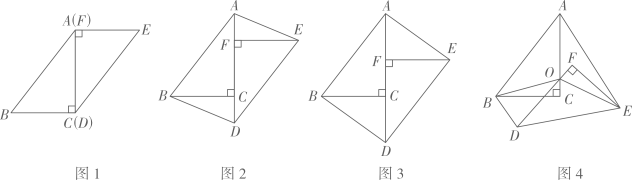(1)、活动一：将图1中的纸片DEF沿AC方向平移，连结AE，BD(如图2)，当点F与点C重合时停止平移。
【思考】图2中的四边形ABDE是平行四边形吗？请说明理由。

【发现】当纸片DEF平移到某一位置时，小兵发现四边形AB DE为矩形(如图3)。求AF的长。

(2)、活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90)，连结OB，OE(如图4)。
【探究】当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由。

查看试题解析
19. 在 6×6 的方格纸中，点 A，B，C 都在格点上，按要求画图：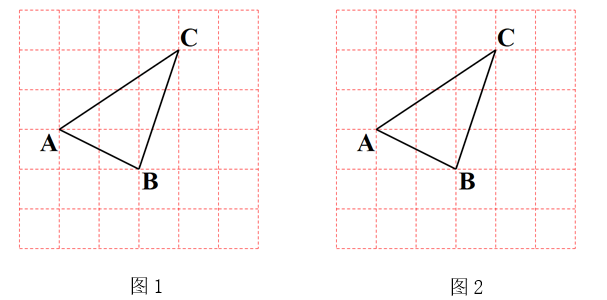

(1)、在图1中找一个格点D，使以点 A，B，C，D 为顶点的四边形是平行四边形．

(2)、在图2中仅用无刻度的直尺，把线段AB 三等分（保留画图痕迹，不写画法）．

查看试题解析
20. 如图，已知在△ABC中，D，E，F分别是AB，BC，AC的中点，连结DF，EF，BF.

(1)、求证：四边形BEFD是平行四边形；

(2)、若∠AFB＝90°，AB＝6，求四边形BEFD的周长.

查看试题解析
21. 已知在Rt△ABC中，∠BAC=90°，AB≥AC，D，E分别为AC，BC边上的点（不包括端点），且 $\frac{D C}{B E} = \frac{A C}{B C}$ =m，连结AE，过点D作DM⊥AE，垂足为点M，延长DM交AB于点F．

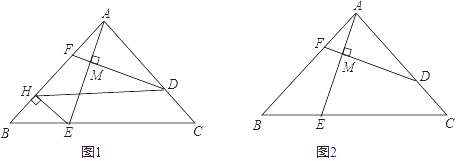(1)、如图1，过点E作EH⊥AB于点H，连结DH．
①求证：四边形DHEC是平行四边形；
②若m= $\frac{\sqrt{2}}{2}$ ，求证：AE=DF；

(2)、如图2，若m= $\frac{3}{5}$ ，求 $\frac{D F}{A E}$ 的值．

查看试题解析
22. 如图1，窗框和窗扇用“滑块铰链”连接.图3是图2中“滑块铰链”的平面示意图，滑轨 $M N$ 安装在窗框上，托悬臂 $D E$ 安装在窗扇上，交点 $A$ 处装有滑块，滑块可以左右滑动，支点 $B$ ， $C$ ， $D$ 始终在一直线上，延长 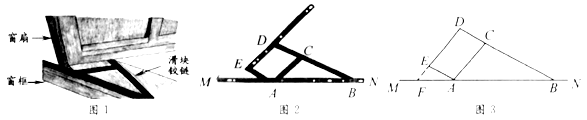$D E$ 交 $M N$ 于点 $F$ .已知 $A C = D E = 20 c m$ ， $A E = C D = 10 c m$ ， $B D = 40 c m$ .

(1)、窗扇完全打开，张角 $∠ C A B = 85^{\circ}$ ，求此时窗扇与窗框的夹角 $∠ D F B$ 的度数.

(2)、窗扇部分打开，张角 $∠ C A B = 60^{\circ}$ ，求此时点 $A$ ， $B$ 之间的距离（精确到 $0.1 c m$ ）.
（参考数据： $\sqrt{3} \approx 1.732$ ， $\sqrt{6} \approx 2.449$ ）

查看试题解析
23. 如图1，窗框和窗扇用“滑块铰链”连接。图3是图2中“滑块铰链”的平面示意图，滑轨MN安装在窗框上，托悬臂DE安装在窗扇上，交点A处装有滑块，滑块可以左右滑动，支点B，C，D始终在一直线上，延长DE交MN于点F。已知AC=DE=20cm，AE=CD=10cm，BD=40cm。

(1)、窗扇完全打开，张角∠CAB=85°，求此时窗扇与窗框的夹角∠DFB的度数。

(2)、窗扇部分打开，张角∠CAB=60°，求此时点A，B之间的距离（精确到0.1cm）。
（参考数据： $\sqrt{3}$ ≈1.732， $\sqrt{6}$ ≈2.449）

查看试题解析
24. 已知在平面直角坐标系xOy中，点A是反比例函数 $y = \frac{1}{x} (x > 0)$ 图像上的一个动点，连结AO，AO的延长线交反比例函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x < 0$ ）的图像于点B，过点A作AE⊥ $y$ 轴于点E。

(1)、如图1，过点B作BF⊥ $x$ 轴于点F，连结EF，
①若 $k = 1$ ，求证：四边形AEFO是平行四边形；

②连结BE，若 $k = 4$ ，求△BOE的面积。

(2)、如图2，过点E作EP∥AB，交反比例函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x < 0$ ）的图像于点P，连结OP。
试探究：对于确定的实数 $k$ ，动点A在运动过程中，△POE的面积是否会发生变化？请说明理由。

查看试题解析
25. 如图，在△ABC中，∠BAC＝90°，点E在BC边上，且CA＝CE，过A，C，E三点的⊙O交AB于另一点F，作直径AD，连结DE并延长交AB于点G，连结CD，CF．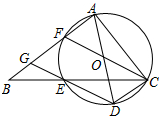

(1)、求证：四边形DCFG是平行四边形；

(2)、当BE＝4，CD＝ $\frac{3}{8}$ AB时，求⊙O的直径长．

查看试题解析