浙江省历年(2018-2022年)真题分类汇编专题30 三角形的中位线定理
试卷更新日期:2022-08-14 类型:二轮复习
一、单选题
-
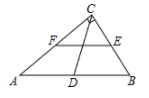
1. 如图,在Rt△ABC中,D为斜边AC的中点,E为BD上一点,F为CE中点.若AE=AD,DF=2,则BD的长为( )
 A、 B、3 C、 D、42. 如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )
A、 B、3 C、 D、42. 如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )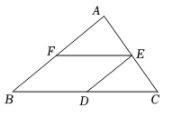 A、28 B、14 C、10 D、73. 如图,在 中, , , ,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( )
A、28 B、14 C、10 D、73. 如图,在 中, , , ,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( ) A、6 B、9 C、12 D、154. 如图,在 中, 于点D, .若E,F分别为 , 的中点,则 的长为( )
A、6 B、9 C、12 D、154. 如图,在 中, 于点D, .若E,F分别为 , 的中点,则 的长为( )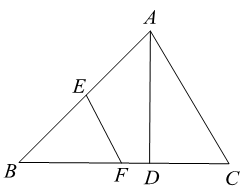 A、 B、 C、1 D、5. 如图是一个由5张纸片拼成的 ,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为 ,另两张直角三角形纸片的面积都为 ,中间一张矩形纸片 的面积为 , 与 相交于点O.当 的面积相等时,下列结论一定成立的是( )
A、 B、 C、1 D、5. 如图是一个由5张纸片拼成的 ,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为 ,另两张直角三角形纸片的面积都为 ,中间一张矩形纸片 的面积为 , 与 相交于点O.当 的面积相等时,下列结论一定成立的是( )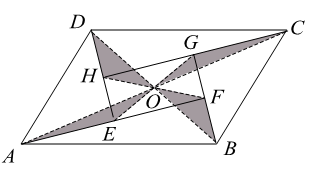 A、 B、 C、 D、6. 如图,已知在△ABC中,∠ABC<90°,AB≠BC,BE是AC边上的中线。按下列步骤作图:
A、 B、 C、 D、6. 如图,已知在△ABC中,∠ABC<90°,AB≠BC,BE是AC边上的中线。按下列步骤作图:①分别以点B,C为圆心,大于线段BC长度一半的长为半径作弧,相交于点M,N;②过点M,N作直线MN,分别交BC,BE于点D,O;③连结CO,DE。则下列结论错误的是( )
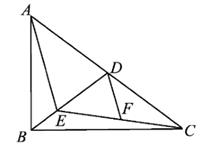
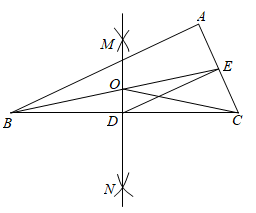 A、OB=OC B、∠BOD=∠COD C、DE∥AB D、DB=DE7. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连结DE,F为DE中点,连结BF.若AC=8,BC=6,则BF的长为( )
A、OB=OC B、∠BOD=∠COD C、DE∥AB D、DB=DE7. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连结DE,F为DE中点,连结BF.若AC=8,BC=6,则BF的长为( )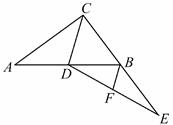 A、2 B、2.5 C、3 D、48. 如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )
A、2 B、2.5 C、3 D、48. 如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( ) A、AE=EF B、AB=2DE C、△ADF和△ADE的面积相等 D、△ADE和△FDE的面积相等9.
A、AE=EF B、AB=2DE C、△ADF和△ADE的面积相等 D、△ADE和△FDE的面积相等9.一张矩形纸片 ,已知 , ,小明按所给图步骤折叠纸片,则线段 长为( )
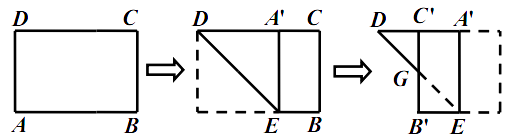 A、 B、 C、 D、10. 如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A',B',A'E与BC相交于点G,B'A'的延长线过点C,若 ,则 的值为( )
A、 B、 C、 D、10. 如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A',B',A'E与BC相交于点G,B'A'的延长线过点C,若 ,则 的值为( )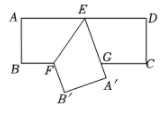 A、 B、 C、 D、11. 由四个全等的直角三角形和一个小正方形组成的大正方形 如图所示.过点 作 的垂线交小正方形对角线 的延长线于点 ,连结 ,延长 交 于点 .若 ,则 的值为( )
A、 B、 C、 D、11. 由四个全等的直角三角形和一个小正方形组成的大正方形 如图所示.过点 作 的垂线交小正方形对角线 的延长线于点 ,连结 ,延长 交 于点 .若 ,则 的值为( ) A、 B、 C、 D、12. 如图,在△ABC中,∠BAC=90°,AB=AC=5,点D在AC上,且AD=2,点E是AB上的动点,连结DE , 点F , G分别是BC和DE的中点,连结AG , FG , 当AG=FG时,线段DE长为( )
A、 B、 C、 D、12. 如图,在△ABC中,∠BAC=90°,AB=AC=5,点D在AC上,且AD=2,点E是AB上的动点,连结DE , 点F , G分别是BC和DE的中点,连结AG , FG , 当AG=FG时,线段DE长为( )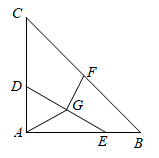 A、 B、 C、 D、4
A、 B、 C、 D、4二、填空题