浙江省历年(2018-2022年)真题分类汇编专题28 勾股定理
试卷更新日期:2022-08-14 类型:二轮复习
一、单选题
-
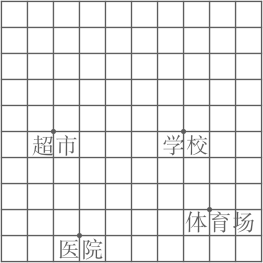
1. 如图是城市某区域的示意图,建立平面直角坐标系后,学校和体育场的坐标分别是(3,1),(4,-2),下列各地点中,离原点最近的是( )
 A、超市 B、医院 C、体育场 D、学校2. 已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;②作∠BAC的平分线AD;③以点A为圆心,AB长为半径作弧,交AD于点E;④过点E作EP⊥AB于点P,则AP:AB=( )
A、超市 B、医院 C、体育场 D、学校2. 已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;②作∠BAC的平分线AD;③以点A为圆心,AB长为半径作弧,交AD于点E;④过点E作EP⊥AB于点P,则AP:AB=( )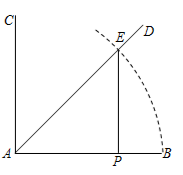 A、 B、 C、 D、3. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( )
A、 B、 C、 D、3. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( ) A、 B、 C、 D、4. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连结DE,F为DE中点,连结BF.若AC=8,BC=6,则BF的长为( )
A、 B、 C、 D、4. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连结DE,F为DE中点,连结BF.若AC=8,BC=6,则BF的长为( )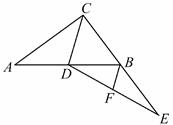 A、2 B、2.5 C、3 D、45. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A、2 B、2.5 C、3 D、45. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
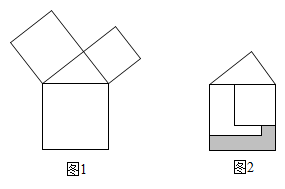 A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和6. 欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是;画Rt△ABC,使∠ACB=90°,BC= ,AC=b,再在斜边AB上截取BD= 。则该方程的一个正根是( )
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和6. 欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是;画Rt△ABC,使∠ACB=90°,BC= ,AC=b,再在斜边AB上截取BD= 。则该方程的一个正根是( )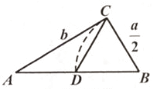 A、AC的长 B、AD的长 C、BC的长 D、CD的长7. 如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A',B',A'E与BC相交于点G,B'A'的延长线过点C,若 ,则 的值为( )
A、AC的长 B、AD的长 C、BC的长 D、CD的长7. 如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A',B',A'E与BC相交于点G,B'A'的延长线过点C,若 ,则 的值为( )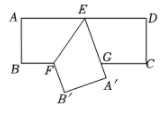 A、 B、 C、 D、8. 由四个全等的直角三角形和一个小正方形组成的大正方形 如图所示.过点 作 的垂线交小正方形对角线 的延长线于点 ,连结 ,延长 交 于点 .若 ,则 的值为( )
A、 B、 C、 D、8. 由四个全等的直角三角形和一个小正方形组成的大正方形 如图所示.过点 作 的垂线交小正方形对角线 的延长线于点 ,连结 ,延长 交 于点 .若 ,则 的值为( ) A、 B、 C、 D、9. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH . 连结EG,BD相交于点O,BD与HC相交于点P.若GO=GP,则 的值是( )
A、 B、 C、 D、9. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH . 连结EG,BD相交于点O,BD与HC相交于点P.若GO=GP,则 的值是( )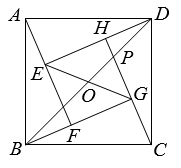 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 如图,木工用角尺的短边紧靠⊙О于点A,长边与⊙О相切于点B,角尺的直角顶点为C,已知AC=6cm,CB=8cm,则⊙О的半径为cm.
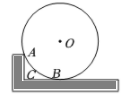 11. 如图,在直角坐标系中,△ABC的顶点C与原点O重合,点A在反比例函数y= (k>0,x>0)的图象上,点B的坐标为(4,3),AB与y轴平行,若AB=BC,则k= .
11. 如图,在直角坐标系中,△ABC的顶点C与原点O重合,点A在反比例函数y= (k>0,x>0)的图象上,点B的坐标为(4,3),AB与y轴平行,若AB=BC,则k= . 12. 如图,已知⊙O的半径为1,点P是⊙O外一点,且OP=2。若PT是⊙O的切线,T为切点,连结OT,则PT=
12. 如图,已知⊙O的半径为1,点P是⊙O外一点,且OP=2。若PT是⊙O的切线,T为切点,连结OT,则PT=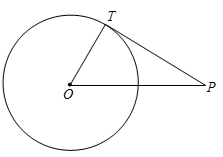 13. 如图,在▱ABCD中,对角线AC , BD交于点O , AB⊥AC , AH⊥BD于点H , 若AB=2,BC=2 ,则AH的长为 .
13. 如图,在▱ABCD中,对角线AC , BD交于点O , AB⊥AC , AH⊥BD于点H , 若AB=2,BC=2 ,则AH的长为 .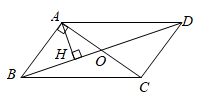 14. 如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(片在结合部分不重叠无缝隙),则图2中阴影部分面积为。
14. 如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(片在结合部分不重叠无缝隙),则图2中阴影部分面积为。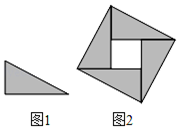 15. 如图,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连结OC,AC.当△OAC是直角三角形时,其斜边长为.
15. 如图,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连结OC,AC.当△OAC是直角三角形时,其斜边长为.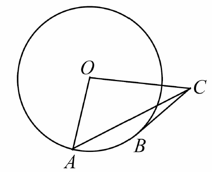 16. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形ABCD的边为斜边,向内作四个全等的直角三角形,使四个直角顶点E,F,G,H都是格点,且四边形EFGH为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形ABCD的边长为 ,此时正方形EFGH的面积为5.问:当格点弦图中的正方形ABCD的边长为 时,正方形EFGH的面积的所有可能值是(不包括5).
16. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形ABCD的边为斜边,向内作四个全等的直角三角形,使四个直角顶点E,F,G,H都是格点,且四边形EFGH为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形ABCD的边长为 ,此时正方形EFGH的面积为5.问:当格点弦图中的正方形ABCD的边长为 时,正方形EFGH的面积的所有可能值是(不包括5).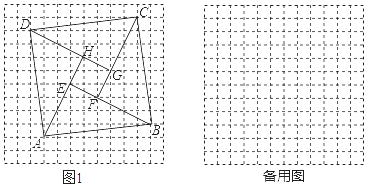 17. 如图,直线 与 轴、 轴分别交于A,B两点,C是OB的中点,D是AB上一点,四边形OEDC是菱形,则△OAE的面积为 .
17. 如图,直线 与 轴、 轴分别交于A,B两点,C是OB的中点,D是AB上一点,四边形OEDC是菱形,则△OAE的面积为 . 18. 折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在直线AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=。
18. 折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在直线AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=。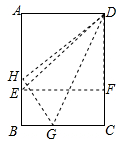 19. 图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的 的值为;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为.
19. 图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的 的值为;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为.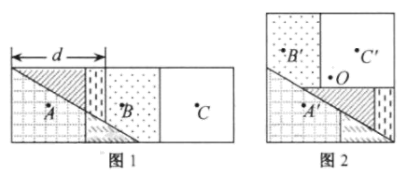 20. 七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”. 由边长为4√2的正方形ABCD可以制作一副如图1所示的七巧板,现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型(其中点Q、R分别与图2中的点E、G重合,点P在边EH上),则“拼搏兔”所在正方形EFGH的边长是.
20. 七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”. 由边长为4√2的正方形ABCD可以制作一副如图1所示的七巧板,现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型(其中点Q、R分别与图2中的点E、G重合,点P在边EH上),则“拼搏兔”所在正方形EFGH的边长是.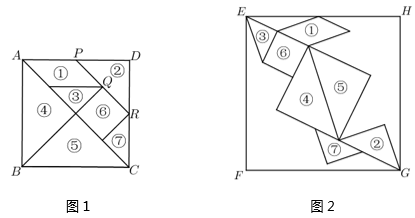 21. 如图,在正方形 中, ,点 , 分别在 , 上, , , 相交于点 .若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为 .
21. 如图,在正方形 中, ,点 , 分别在 , 上, , , 相交于点 .若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为 .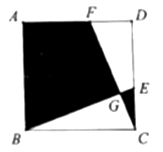
三、作图题
-
22. 如图,在7×5的方格纸ABCD中,请按要求画图,且所画格点三角形与格点四边形的顶点均不与点A,B,C,D重合.
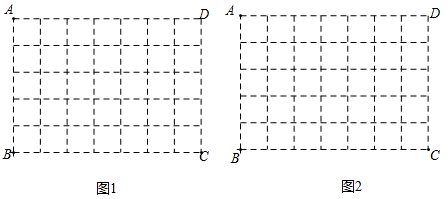 (1)、在图1中画一个格点△EFG,使点E,F,G分别落在边AB,BC,CD上,且∠EFG=90°;(2)、在图2中画一个格点四边形MNPQ,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且MP=NQ.
(1)、在图1中画一个格点△EFG,使点E,F,G分别落在边AB,BC,CD上,且∠EFG=90°;(2)、在图2中画一个格点四边形MNPQ,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且MP=NQ.四、综合题
-
23. 如图,将矩形纸片ABCD折叠,使点B与点D重台,点A落在点P处,折痕为EF,
 (1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长.24. 如图,在△ABC中,∠ACB=90°,以点B为圆心,BC的长为半径画弧,交线段AB于点D,以点A为圆心,AD长为半径画弧,交线段AC于点E,连结CD。
(1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长.24. 如图,在△ABC中,∠ACB=90°,以点B为圆心,BC的长为半径画弧,交线段AB于点D,以点A为圆心,AD长为半径画弧,交线段AC于点E,连结CD。 (1)、若∠A=28°,求∠ACD的度数;(2)、设BC=a,AC=b;
(1)、若∠A=28°,求∠ACD的度数;(2)、设BC=a,AC=b;①线段AD的长度是方程 的一个根吗?说明理由。
②若线段AD=EC,求 的值.
25. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”。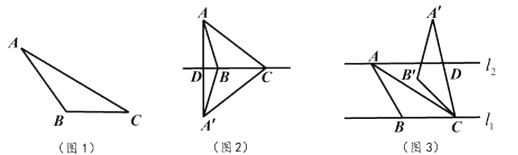 (1)、概念理解:如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是“等高底”三角形请说明理由。(2)、问题探究:如图2,△ABC是“等高底”三角形,BC是“等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA'交直线BC于点D.若点B是△AA'C的重心,求 的值.(3)、应用拓展:如图3.已知l1∥l2 , l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,AC所在直线交l2于点D.求CD的值。
(1)、概念理解:如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是“等高底”三角形请说明理由。(2)、问题探究:如图2,△ABC是“等高底”三角形,BC是“等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA'交直线BC于点D.若点B是△AA'C的重心,求 的值.(3)、应用拓展:如图3.已知l1∥l2 , l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,AC所在直线交l2于点D.求CD的值。
-