浙江省历年(2018-2022年)真题分类汇编专题27 三角形的全等及其判定(2)
试卷更新日期:2022-08-14 类型:二轮复习
一、单选题
-
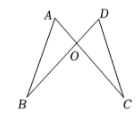
1. 如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )
 A、SSS B、SAS C、AAS D、HL2. 如图,在 中, ,以该三角形的三条边为边向形外作正方形,正方形的顶点 都在同一个圆上.记该圆面积为 , 面积为 ,则 的值是( )
A、SSS B、SAS C、AAS D、HL2. 如图,在 中, ,以该三角形的三条边为边向形外作正方形,正方形的顶点 都在同一个圆上.记该圆面积为 , 面积为 ,则 的值是( ) A、 B、 C、 D、3. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点P是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值是( )
A、 B、 C、 D、3. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点P是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值是( )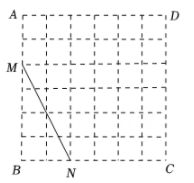 A、 B、6 C、 D、4. △BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )
A、 B、6 C、 D、4. △BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )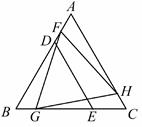 A、△ABC的周长 B、△AFH的周长 C、四边形FBGH的周长 D、四边形ADEC的周长5. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH . 连结EG,BD相交于点O,BD与HC相交于点P.若GO=GP,则 的值是( )
A、△ABC的周长 B、△AFH的周长 C、四边形FBGH的周长 D、四边形ADEC的周长5. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH . 连结EG,BD相交于点O,BD与HC相交于点P.若GO=GP,则 的值是( )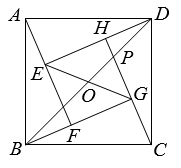 A、 B、 C、 D、6. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )
A、 B、 C、 D、6. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )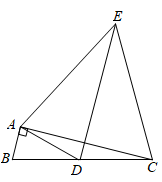 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
7. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 ,椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得 , , .
 (1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角 的度数达到最小值 时,A,B两点间的距离为cm(结果精确到0.1cm).(参考数据: , , )8. 如图,在平面直角坐标系中,正方形ABCD的顶点A在x轴正半轴上,顶点B,C在第一象限,顶点D的坐标 . 反比例函数 (常数 , )的图象恰好经过正方形ABCD的两个顶点,则k的值是.
(1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角 的度数达到最小值 时,A,B两点间的距离为cm(结果精确到0.1cm).(参考数据: , , )8. 如图,在平面直角坐标系中,正方形ABCD的顶点A在x轴正半轴上,顶点B,C在第一象限,顶点D的坐标 . 反比例函数 (常数 , )的图象恰好经过正方形ABCD的两个顶点,则k的值是.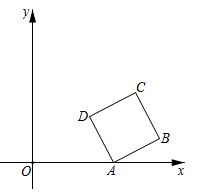 9. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.
9. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.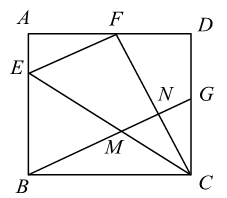 10. 如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y= ,则图象经过点D的反比例函数的解析式是 .
10. 如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y= ,则图象经过点D的反比例函数的解析式是 .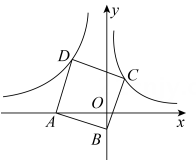
三、作图题
-
11. 如图,在 的网格中, 的三个顶点都在格点上.
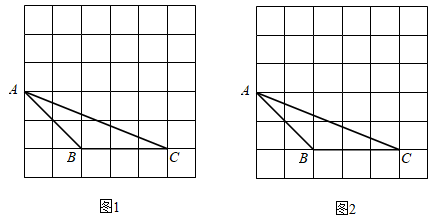 (1)、在图1中画出 ,使 与 全等,顶点D在格点上.(2)、在图2中过点B画出平分 面积的直线l.
(1)、在图1中画出 ,使 与 全等,顶点D在格点上.(2)、在图2中过点B画出平分 面积的直线l.四、解答题
-
12. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .
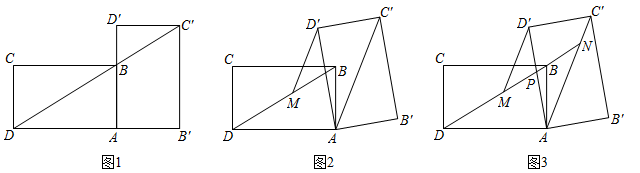
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.
五、综合题
-
13. 如图,在四边形ABCD中,AB=AD=20,BC=DC=10 .
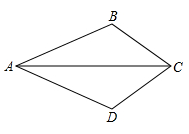 (1)、求证:△ABC≌△ADC;(2)、当∠BCA=45°时,求∠BAD的度数.14. 如图
(1)、求证:△ABC≌△ADC;(2)、当∠BCA=45°时,求∠BAD的度数.14. 如图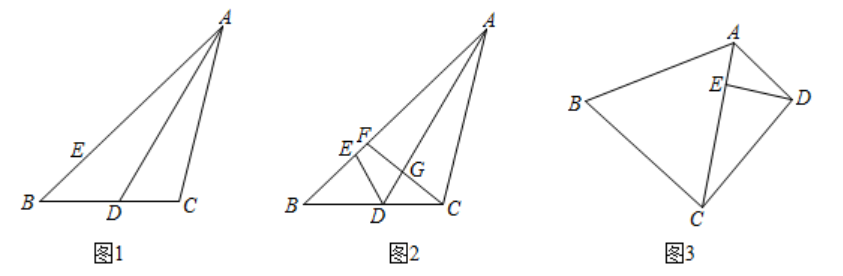 (1)、(证明体验)
(1)、(证明体验)如图1, 为 的角平分线, ,点E在 上, .求证: 平分 .
(2)、(思考探究)如图2,在(1)的条件下,F为 上一点,连结 交 于点G.若 , , ,求 的长.
(3)、(拓展延伸)如图3,在四边形 中,对角线 平分 ,点E在 上, .若 ,求 的长.
15. 图1中有四条优美的“螺旋折线”,它们是怎样画出来的呢?如图2,在正方形 ABCD 各边上分别取点 B1,C1 , D1 , A1 , 使 AB1=BC1=CD1=DA1=AB,依次连接它们,得到四边形A1B1C1D1 ;再在四边形A1B1C1D1各边上分别取点 B2 , C2 , D2 , A2 , 使A1B2=B1C2=C1D2=D1A2=A1B1 , 依次连接它们,得到四边形 A2B2C2D2 ;…如此继续下去,得到四条螺旋折线.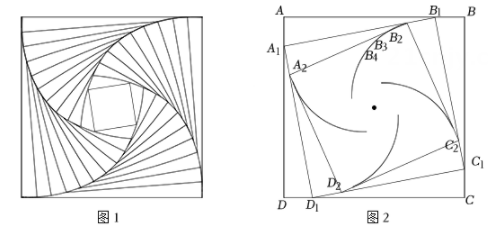 (1)、求证:四边形A1B1C1D1 是正方形;(2)、求 的值;(3)、请研究螺旋折线BB1B2B3 …中相邻线段之间的关系,写出一个正确结论并加以证明.16. 如图,将矩形纸片ABCD折叠,使点B与点D重台,点A落在点P处,折痕为EF,
(1)、求证:四边形A1B1C1D1 是正方形;(2)、求 的值;(3)、请研究螺旋折线BB1B2B3 …中相邻线段之间的关系,写出一个正确结论并加以证明.16. 如图,将矩形纸片ABCD折叠,使点B与点D重台,点A落在点P处,折痕为EF, (1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长.17. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G.
(1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长.17. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G.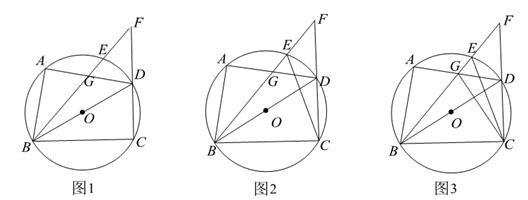 (1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .
(1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .①若 ,求 的周长.
②求 的最小值.
18. 已知在Rt△ABC中,∠ACB=90°,a,b分别表示∠A,∠B的对边,a>b.记△ABC的面积为S.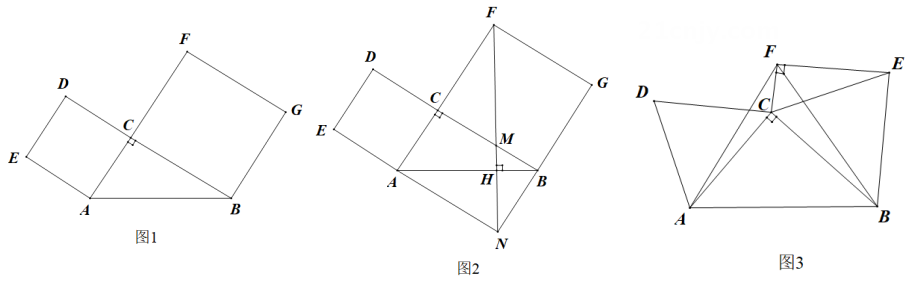 (1)、如图1,分别以AC,CB为边向形外作正方形ACDE和正方形BGFC.记正方形ACDE的面积为S1 , 正方形BGFC的面积为S2 .
(1)、如图1,分别以AC,CB为边向形外作正方形ACDE和正方形BGFC.记正方形ACDE的面积为S1 , 正方形BGFC的面积为S2 .①若S1=9,S2=16,求S的值;
②延长EA交GB的延长线于点N,连结FN,交BC于点M,交AB于点H.若FH⊥AB(如图2所示),求证:S2-S1=2S.
(2)、如图3,分别以AC,CB为边向形外作等边三角形ACD和等边三角形CBE,记等边三角形ACD的面积为S1 , 等边三角形CBE的面积为S2 . 以AB为边向上作等边三角形ABF(点C在△ABF内),连结EF,CF.若EF⊥CF,试探索S2-S1与S之间的等量关系,并说明理由.19. 在正方形ABCD中,点M是边AB的中点,点E在线段AM上(不与点A重合),点F在边BC上,且AE=2BF,连接EF,以EF为边在正方形ABCD内作正方形EFGH.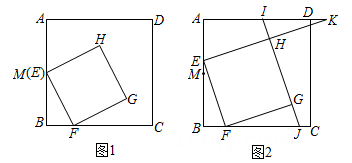 (1)、如图1.若AB=4,当点E与点M重合时,求正方形EFGH的面积(2)、如图2.已知直线HG分别与边AD,BC交于点I,J,射线EH与射线AD交于点K.
(1)、如图1.若AB=4,当点E与点M重合时,求正方形EFGH的面积(2)、如图2.已知直线HG分别与边AD,BC交于点I,J,射线EH与射线AD交于点K.①求证:EK=2EH;
②设∠AEK=α,△FGJ和四边形AEHI的面积分别为S1、S2 .
求证: =4sin2α-1.
-
-