浙江省历年(2018-2022年)真题分类汇编专题27 三角形的全等及其判定(1)
试卷更新日期:2022-08-14 类型:二轮复习
一、单选题
-
1. 如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , ,将 沿直线 折叠,得到 ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是( )
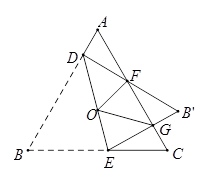 A、 B、 的周长是一个定值 C、四边形 的面积是一个定值 D、四边形 的面积是一个定值2. 如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为( )
A、 B、 的周长是一个定值 C、四边形 的面积是一个定值 D、四边形 的面积是一个定值2. 如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为( )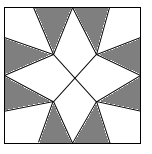 A、 :1 B、3:2 C、 :1 D、 :2
A、 :1 B、3:2 C、 :1 D、 :2二、填空题
-
3. 等腰三角形 中,顶角 为 ,点 在以 为圆心, 长为半径的圆上,且 ,则 的度数为 .4. 等腰三角形ABC中,顶角A为40°,点P在以A为圆心,BC长为半径的圆上,且BP=BA,则∠PBC的度数为。5. 如图,△ABC的两条高AD , BE相交于点F , 请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是 .
 6. 如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是(只需写一个,不添加辅助线)
6. 如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是(只需写一个,不添加辅助线)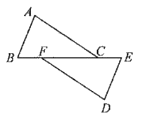 7. 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b. 依次连接四块大正方形地砖的中心得到正方形ABCD. 则正方形ABCD的面积为. (用含a,b的代数式表示)
7. 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b. 依次连接四块大正方形地砖的中心得到正方形ABCD. 则正方形ABCD的面积为. (用含a,b的代数式表示) 8. 如图,在正方形 中, ,点 , 分别在 , 上, , , 相交于点 .若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为 .
8. 如图,在正方形 中, ,点 , 分别在 , 上, , , 相交于点 .若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为 .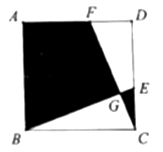 9. 如图,在菱形ABCD中,AB=2,∠B是锐角,AE⊥BC于点E,M是AB的中点,连结MD,ME.若∠EMD=90°,则cosB的值为。
9. 如图,在菱形ABCD中,AB=2,∠B是锐角,AE⊥BC于点E,M是AB的中点,连结MD,ME.若∠EMD=90°,则cosB的值为。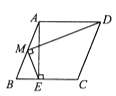 10. 图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为分米.
10. 图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为分米.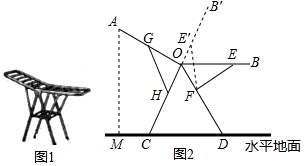
三、作图题
-
11. 如图,在4×4的方格子中,△ABC的三个顶点都在格点上,
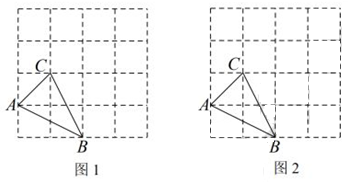 (1)、在图1中画出线段CD,使CD⊥CB,其中D是格点,(2)、在图2中画出平行四边形ABEC,其中E是格点.
(1)、在图1中画出线段CD,使CD⊥CB,其中D是格点,(2)、在图2中画出平行四边形ABEC,其中E是格点.四、解答题
-
12. 如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°。
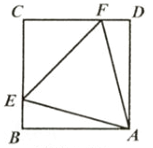
求证:矩形ABCD是正方形
13. 如图,在正方形ABCD中,点G在边BC上(不与点B,C重合),连接AG,作DE⊥AG,于点E,BF⊥AG于点F,设 。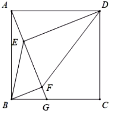 (1)、求证:AE=BF;(2)、连接BE,DF,设∠EDF= ,∠EBF= 求证:(3)、设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2 , 求 的最大值.14. 已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF。
(1)、求证:AE=BF;(2)、连接BE,DF,设∠EDF= ,∠EBF= 求证:(3)、设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2 , 求 的最大值.14. 已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF。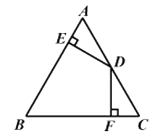
求证:△ABC是等边三角形。
15. 如图,在▱ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F。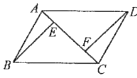
求证:AE=CF。
16. 如图,在矩形 ABCD中,点 E,F 在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明.
五、综合题
-
17. 已知在Rt△ABC中,∠BAC=90°,AB≥AC,D,E分别为AC,BC边上的点(不包括端点),且 =m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
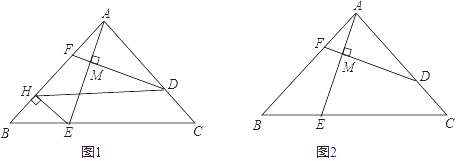 (1)、如图1,过点E作EH⊥AB于点H,连结DH.
(1)、如图1,过点E作EH⊥AB于点H,连结DH.①求证:四边形DHEC是平行四边形;
②若m= ,求证:AE=DF;
(2)、如图2,若m= ,求 的值.18. 如图,在 中, , ,点 , 分别在 , 上,且 .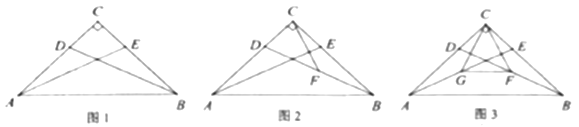 (1)、 如图1,求证: ;(2)、 如图2, 是 的中点.求证: ;(3)、 如图3, , 分别是 , 的中点.若 , ,求 的面积.19. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连结BE.
(1)、 如图1,求证: ;(2)、 如图2, 是 的中点.求证: ;(3)、 如图3, , 分别是 , 的中点.若 , ,求 的面积.19. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连结BE.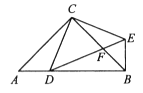 (1)、求证:△ACD≌△BCE;(2)、当AD=BF时,求∠BEF的度数.20. 小敏思考解决如下问题:
(1)、求证:△ACD≌△BCE;(2)、当AD=BF时,求∠BEF的度数.20. 小敏思考解决如下问题:原题:如图1,点 , 分别在菱形 的边 , 上, ,求证: .
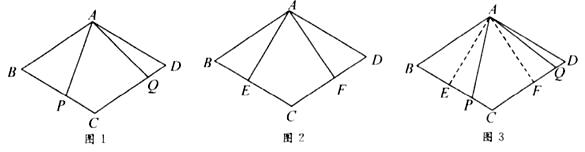 (1)、小敏进行探索,若将点 , 的位置特殊化:把 绕点 旋转得到 ,使 ,点 , 分别在边 , 上,如图2,此时她证明了 .请你证明.(2)、受以上(1)的启发,在原题中,添加辅助线:如图3,作 , ,垂足分别为 , .请你继续完成原题的证明.(3)、如果在原题中添加条件: , ,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).21. 如图,在四边形ABCD中,E是AB的中点,AD//EC,∠AED=∠B.
(1)、小敏进行探索,若将点 , 的位置特殊化:把 绕点 旋转得到 ,使 ,点 , 分别在边 , 上,如图2,此时她证明了 .请你证明.(2)、受以上(1)的启发,在原题中,添加辅助线:如图3,作 , ,垂足分别为 , .请你继续完成原题的证明.(3)、如果在原题中添加条件: , ,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).21. 如图,在四边形ABCD中,E是AB的中点,AD//EC,∠AED=∠B.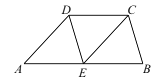 (1)、求证:△AED≌△EBC.(2)、当AB=6时,求CD的长.22. 如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在上.
(1)、求证:△AED≌△EBC.(2)、当AB=6时,求CD的长.22. 如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在上.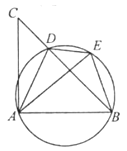 (1)、求证:AE=AB.(2)、若∠CAB=90°,cos∠ADB= ,BE=2,求BC的长.23. 小敏思考解决如下问题:
(1)、求证:AE=AB.(2)、若∠CAB=90°,cos∠ADB= ,BE=2,求BC的长.23. 小敏思考解决如下问题:原题:如图1,点P,Q分别在菱形ABCD的边BC,CD上,∠PAQ=∠B,求证AP=AQ。
 (1)、小敏进行探索,若将点P,Q的位置特殊化:把∠PAQ绕点A旋转得到∠EAF,使AE⊥BC,点E,F分别在边BC,CD上,如图2,此时她证明了AE=AF。请你证明。(2)、受以上(1)的启发,在原题中,添加辅助线:如图3,作AE⊥BC,AF⊥CD,垂足分别为E,F。请你继续完成原题的证明。(3)、如果在原题中添加条件:AB=4,∠B=60°,如图1,请你编制一个计算题(不标注新的字母),并直接给出答案。24. 如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)、小敏进行探索,若将点P,Q的位置特殊化:把∠PAQ绕点A旋转得到∠EAF,使AE⊥BC,点E,F分别在边BC,CD上,如图2,此时她证明了AE=AF。请你证明。(2)、受以上(1)的启发,在原题中,添加辅助线:如图3,作AE⊥BC,AF⊥CD,垂足分别为E,F。请你继续完成原题的证明。(3)、如果在原题中添加条件:AB=4,∠B=60°,如图1,请你编制一个计算题(不标注新的字母),并直接给出答案。24. 如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F. (1)、求证:△BDE≌△CDF;(2)、当AD⊥BC,AE=1,CF=2时,求AC的长.25. 如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
(1)、求证:△BDE≌△CDF;(2)、当AD⊥BC,AE=1,CF=2时,求AC的长.25. 如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.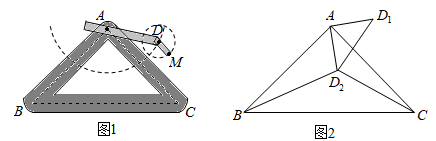 (1)、在旋转过程中,
(1)、在旋转过程中,①当A,D,M三点在同一直线上时,求AM的长。
②当A,D,M三点为同一直角三角形的顶点时,求AM的长。
(2)、若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2 , 如图2.此时∠AD2C=135°,CD2=60,求BD2的长.26. 如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F、H在菱形ABCD的对角线BD上.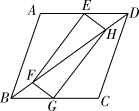 (1)、求证:BG=DE;(2)、若E为AD中点,FH=2,求菱形ABCD的周长。27. 如图,已知AB=AC,AD=AE,BD和CE相交于点O.
(1)、求证:BG=DE;(2)、若E为AD中点,FH=2,求菱形ABCD的周长。27. 如图,已知AB=AC,AD=AE,BD和CE相交于点O.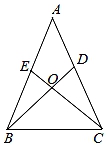 (1)、求证:△ABD≌△ACE;(2)、判断△BOC的形状,并说明理由.28. 如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE。
(1)、求证:△ABD≌△ACE;(2)、判断△BOC的形状,并说明理由.28. 如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE。 (1)、求证:△ABC≌△DCE(2)、连结AE,当BC=5,AC=12时,求AE的长。29. 如图,点E是 ABCD的边CD的中点,连结AE并延长,交BC的延长线于点F。
(1)、求证:△ABC≌△DCE(2)、连结AE,当BC=5,AC=12时,求AE的长。29. 如图,点E是 ABCD的边CD的中点,连结AE并延长,交BC的延长线于点F。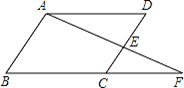 (1)、若AD的长为2,求CF的长。(2)、若∠BAF=90°,试添加一个条件,并写出∠F的度数。30. 在一次数学研究性学习中, 小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1) ,其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动。
(1)、若AD的长为2,求CF的长。(2)、若∠BAF=90°,试添加一个条件,并写出∠F的度数。30. 在一次数学研究性学习中, 小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1) ,其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动。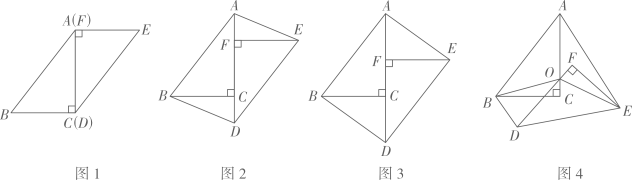 (1)、活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移。
(1)、活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移。【思考】图2中的四边形ABDE是平行四边形吗?请说明理由。
【发现】当纸片DEF平移到某一位置时,小兵发现四边形AB DE为矩形(如图3)。求AF的长。
(2)、活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4)。【探究】当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由。
31. 如图,矩形ABCD中,AB=a,BC=b,点M,N分别在边AB,CD上,点E,F分别在边BC,AD上,MN,EF交于点P,记k=MN:EF.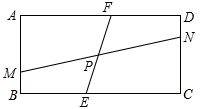 (1)、若a:b的值为1,当MN⊥EF时,求k的值。(2)、若a:b的值为 ,求k的最大值和最小值。(3)、若k的值为3,当点N是矩形的顶点,∠MPE=60°,MP=EF=3PE时,求a:b为的值。32. 我们知道,各个角都相等,各条边都相等的多边形叫做正多边形,对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形
(1)、若a:b的值为1,当MN⊥EF时,求k的值。(2)、若a:b的值为 ,求k的最大值和最小值。(3)、若k的值为3,当点N是矩形的顶点,∠MPE=60°,MP=EF=3PE时,求a:b为的值。32. 我们知道,各个角都相等,各条边都相等的多边形叫做正多边形,对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形 (1)、已知凸五边形ABCDE的各条边都相等
(1)、已知凸五边形ABCDE的各条边都相等①如图1,若AC=AD=BE=BD=CE,求证:五边形ABCDE是正五边形
②2如图2,若AC=BE=CE,请判断五边形ABCDE是不是正五边形,并说明理由
(2)、判断下列命题的真假,(在括号内填写“真”或“假”),如图3,已知凸六边形ABCDEF的各条边都相等①若AC=CE=EA,则六边形ABCDEF是正六边形()
②若AD=BE=CF,则六边形ABCDEF是正六边形()
33. 小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.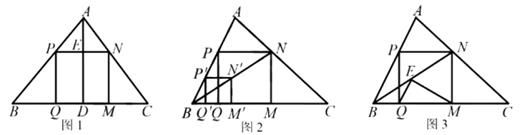
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
(1)、温故:如图1,在△ 中, ⊥ 于点 ,正方形 的边 在 上,顶点 , 分别在 , 上,若 BC=a,AD=h,求正方形 的边长(a,h表示).(2)、操作:如何能画出这个正方形PQMN呢?如图2,小波画出了图1的△ABC,然后按数学家波利亚在《怎样解题》中的方法进行操作,先在AB上任取一点 ,画正方形 ,使 , 在 边上, 在△ 内,然后连结 并延长交 于点N,画 ⊥ 于点 , ⊥ 交 于点 , ⊥ 于点 ,得到四边形P .
推理:证明图2中的四边形 是正方形.
(3)、拓展:小波把图2中的线段BN称为“波利亚线”,在该线截取 ,连结 , (如图3).当∠ =90°时,求“波利亚线”BN的长(用a、h表示).34. 【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E。作DF⊥AE于点H,分别交AB,AC于点F,G。
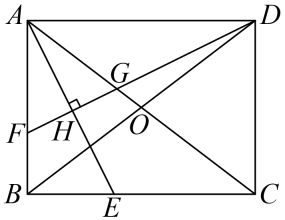 (1)、判断△AFG的形状并说明理由。(2)、求证:BF=2OG。(3)、【迁移应用】
(1)、判断△AFG的形状并说明理由。(2)、求证:BF=2OG。(3)、【迁移应用】记△DGO的面积为S1 , △DBF的面积为S2 , 当 时,求 的值。
(4)、【拓展延伸】若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF。当△BEF的面积为矩形ABCD面积的 时,请直接写出tan∠BAE的值。
-