浙江省历年（2018-2022年）真题分类汇编专题18 反比例函数的图象与性质

试卷更新日期：2022-08-14 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图，点 $A$ ， $B$ 在反比例函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x > 0$ ）的图象上， $A C ⊥ x$ 轴于点 $C$ ， $B D ⊥ x$ 轴于点 $D$ ， $B E ⊥ y$ 轴于点 $E$ ，连结 $A E$ .若 $O E = 1$ ， $O C = \frac{2}{3} O D$ ， $A C = A E$ ，则 $k$ 的值为（）

A、2 B、 $\frac{3 \sqrt{2}}{2}$ C、 $\frac{9}{4}$ D、 $2 \sqrt{2}$

查看试题解析
2. 已知点 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ 在反比例函数 $y = - \frac{12}{x}$ 的图象上.若 $x_{1} < 0 < x_{2}$ ，则（）

A、 $y_{1} < 0 < y_{2}$ B、 $y_{2} < 0 < y_{1}$ C、 $y_{1} < y_{2} < 0$ D、 $y_{2} < y_{1} < 0$

查看试题解析
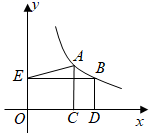3. 已知三个点（x₁ ， y₁），（x₂ ， y₂），（x₃ ， y₃）在反比例函数y＝ $\frac{2}{x}$ 的图象上，其中x₁＜x₂＜0＜x₃ ，下列结论中正确的是（）

A、y₂＜y₁＜0＜y₃ B、y₁＜y₂＜0＜y₃ C、y₃＜0＜y₂＜y₁ D、y₃＜0＜y₁＜y₂

查看试题解析
4. 已知点(－2，a)，(2，b)，(3，c)在函数 $y = \frac{k}{x} (k > 0)$ 的图象上，则下列判断正确的是（）

A、a＜b＜c B、b＜a＜c C、a＜c＜b D、c＜b＜a

查看试题解析
5. 如图，已知直线y=k₁x（k₁≠0）与反比例函数y= $\frac{k_{2}}{x}$ （k₂≠0）的图象交于M，N两点．若点M的坐标是（1，2），则点N的坐标是（）

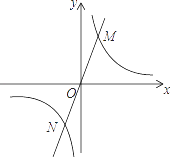A、（﹣1，﹣2） B、（﹣1，2） C、（1，﹣2） D、（﹣2，﹣1）

查看试题解析
6. 如图，点A，B在反比例函数 $y = \frac{1}{x} (x > 0)$ 的图象上，点C，D在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上，AC∥BD∥ $y$ 轴，已知点A，B的横坐标分别为1，2，△OAC与△ABD的面积之和为 $\frac{3}{2}$ ，则 $k$ 的值为（）

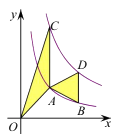A、4 B、3 C、2 D、 $\frac{3}{2}$

查看试题解析
7. 如图，点C在反比例函数 $y = \frac{k}{x}$ （x＞0）的图象上，过点C的直线与x轴，y轴分别交于点A，B，且AB=BC，△AOB的面积为1，则k的值为（）

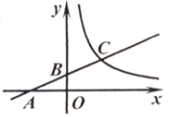A、1 B、2 C、3 D、4

查看试题解析
8. 已知某函数的图象C与函数y= $\frac{3}{x}$ 的图象关于直线y=2对称下列命题：①图象C与函数y= $\frac{3}{x}$ 的象交于点（ $\frac{3}{2}$ ，2）；②（ $\frac{1}{2}$ ，-2）在图象C上；③图象C上的点的纵坐标都小于4；④A（x₁ ， y₁），B（x₂ ， y₂）是图象C上任意两点，若x₁>x₂ ，则y₁-y₂ ，其中真命题是（）

A、①② B、①③④ C、②③④ D、①②③④

查看试题解析
9. 如图，平行于x轴的直线与函数 $y = \frac{k_{1}}{x}$ （k₁＞0，x＞0），y= $\frac{k_{2}}{x}$ （k₂＞0，x＞0）的图像分别交于A，B两点，点A在点B的右侧，C为x轴上的一个动点．若△ABC的面积为4，则k₁-k₂的值为（）

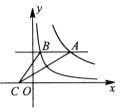A、8 B、-8 C、4 D、-4

查看试题解析

二、填空题

10. 如图，在平面直角坐标系xOy中，点 A （0，4）， B（3，4），将△ABO向右平移到 △CDE 位置， A 的对应点是 C， O的对应点是 E，函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 C 和DE的中点 F，则k的值是．

查看试题解析
11. 如图，在直角坐标系中，△ABC的顶点C与原点O重合，点A在反比例函数y= $\frac{k}{x}$ (k>0，x>0)的图象上，点B的坐标为(4，3)，AB与y轴平行，若AB=BC，则k= ．

查看试题解析
12. 在平面直角坐标系中，对于不在坐标轴上的任意一点 $A (x ， y)$ ，我们把点 $B (\frac{1}{x} ， \frac{1}{y})$ 称为点A的“倒数点”.如图，矩形 $O C D E$ 的顶点C为 $(3 ， 0)$ ，顶点E在y轴上，函数 $y = \frac{2}{x} (x > 0)$ 的图象与 $D E$ 交于点A.若点B是点A的“倒数点”，且点B在矩形 $O C D E$ 的一边上，则 $△ O B C$ 的面积为.

查看试题解析
13. 如图，将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中，AB在x轴上，点G与点A重合，点F在AD上，三角板的直角边EF交BC于点M。反比例函数y= $\frac{k}{x}$ （x>0）的图象恰好经过点F，M。若直尺的宽CD=3，三角板的斜边FG=8 $\sqrt{3}$ ，则k=。

查看试题解析
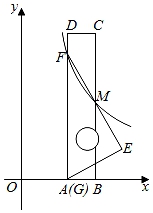14. 点P，Q，R在反比例函数y= $\frac{k}{x}$ (常数k>0，x>0)图象上的位置如图所示，分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S₁ ， S₂ ， S₃；若OE=ED=DC，S₁+S₃=27，则S₂的值为。

查看试题解析
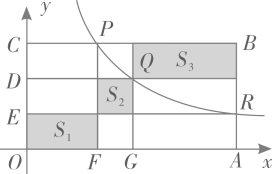15. 如图，已知在平面直角坐标系xOy中，Rt△OAB的直角顶点B在x轴的正半轴上，点A在第一象限，反比例函数 $y = \frac{k}{x}$ (x＞0)的图象经过OA的中点C，交AB于点D，连结CD.若△ACD的面积是2，则k的值是.

查看试题解析
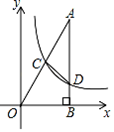16. 如图，矩形ABCD的顶点A，C都在曲线y= $\frac{k}{x}$ （常数k>0，x>0)上，若顶点D的坐标为（5，3），则直线BD的函数表达式是.

查看试题解析
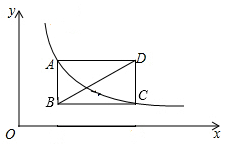17. 过双曲线 $y = \frac{k}{x} (k > 0)$ 的动点 $A$ 作 $A B ⊥ x$ 轴于点 $B$ ， $P$ 是直线 $A B$ 上的点，且满足 $A P = 2 A B$ ，过点 $P$ 作 $x$ 轴的平行线交此双曲线于点 $C$ .如果 $Δ A P C$ 的面积为8，则 $k$ 的值是．

查看试题解析
18. 过双曲线 $y = \frac{k}{x} (k > 0)$ 上的动点A作AB⊥x轴于点B，P是直线AB上的点，且满足AP=2AB，过点P作x轴的平行线交此双曲线于点C，如果△APC的面积为8，则k的值是。

查看试题解析
19. 如图，点A，B是反比例函数 $y = \frac{k}{x} (x > 0)$ 图象上的两点，过点A，B分别作AC⊥x轴于点C，BD⊥x于点D，连接OA，BC，已知点C（2，0），BD＝2，S_△BCD＝3，则S_△AOC＝。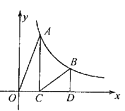

查看试题解析
20. 如图，四边形OABC为矩形，点A在第二象限，点A关于OB的对称点为点D，点B，D都在函数y= $\frac{6 \sqrt{2}}{x}$ (x>0)的图象上，BE⊥x轴于点E．若DC的延长线交x轴于点F，当矩形OABC的面积为 $9 \sqrt{2}$ 时， $\frac{E F}{O E}$ 的值为，点F的坐标为．

查看试题解析
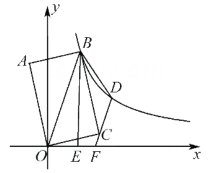21. 如图，已知在平面直角坐标系xOy中，点A在x轴的负半轴上，点B在y轴的负半轴上，tan∠ABO=3，以AB为边向上作正方形ABCD．若图象经过点C的反比例函数的解析式是y= $\frac{1}{x}$ ，则图象经过点D的反比例函数的解析式是．

查看试题解析
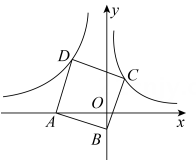22. 如图，在平面直角坐标系中，正方形ABCD的顶点A在x轴正半轴上，顶点B，C在第一象限，顶点D的坐标 $(\frac{5}{2} ， 2)$ . 反比例函数 $y = \frac{k}{x}$ （常数 $k > 0$ ， $x > 0$ ）的图象恰好经过正方形ABCD的两个顶点，则k的值是.

查看试题解析
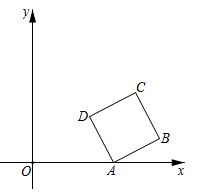23. 如图，经过原点O的直线与反比例函数 $y = \frac{a}{x}$ (a>0)的图象交于A，D两点(点A在第一象限)，点B，C，E在反比例函数 $y = \frac{b}{x}$ (b<0)的图象上，AB∥y轴，AE∥CD∥x轴，五边形ABCDE的面积为56，四边形ABCD的面积为32，则 $a - b$ 的值为， $\frac{b}{a}$ 的值为.

查看试题解析
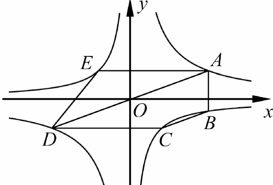24. 如图，在平面直角坐标系中，O为坐标原点， $▱$ ABCD的边AB在x轴上，顶点D在y轴的正半轴上，点C在第一象限，将△AOD沿y轴翻折，使点A落在x轴上的点E处，点B恰好为OE的中点，DE与BC交于点F。若y= $\frac{k}{x}$ （k≠0）图象经过点C，且S△BEF=1，则k的值为。

查看试题解析
25. 如图，过原点的直线与反比例函数y= $\frac{k}{x}$ （k>0)的图象交于A，B两点，点A在第一象限点C在x轴正半轴上，连结AC交反比例函数图象于点D.AE为∠BAC的平分线，过点B作AE的垂线，垂足为E，连结DE.若AC=3DC，△ADE的面积为8，则k的值为.

查看试题解析
26. 如图，已知在平面直角坐标系xOy中，直线 $y = \frac{1}{2} x - 1$ 分别交x轴，y轴于点A和点B，分别交反比例函数 $y_{1} = \frac{k}{x} (k > 0 ， x > 0)$ ， $y_{2} = \frac{2 k}{x} (x < 0)$ 的图象于点C和点D，过点C作CE⊥x轴于点E，连结OC，OD. 若△COE的面积与△DOB的面积相等，则k的值是.

查看试题解析

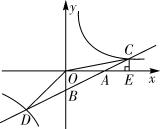
三、综合题

27. 如图，正比例函数y= $- \frac{2}{3}$ x的图象与反比例函数y= $\frac{k}{x}$ (k≠0)的图象都经过点A(a，2)．

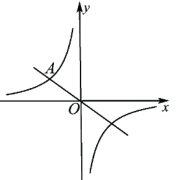(1)、求点A的坐标和反比例函数表达式．

(2)、若点P(m，n)在该反比例函数图象上，且它到y轴距离小于3，请根据图象直接写出n的取值范围．

查看试题解析
28. 已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象的一支如图所示，它经过点（3，-2）．

(1)、求这个反比例函数的表达式，并补画该函数图象的另一支．

(2)、求当 y≤5，且y≠0时自变量x的取值范围．

查看试题解析
29. 如图，点A在第一象限内，AB⊥x轴于点B，反比例函数 $y = \frac{k}{x} (k \neq 0 ， x > 0)$ 的图象分别交AO，AB于点C，D.已知点C的坐标为(2，2)，BD=1.

(1)、求k的值及点D的坐标.

(2)、已知点P在该反比例函数图象上，且在△ABO的内部（包括边界），直接写出点P的横坐标x的取值范围.

查看试题解析
30. 在直角坐标系中，设函数 $y_{1} = \frac{k_{1}}{x}$ （ $k_{1}$ 是常数， $k_{1} > 0$ ， $x > 0$ ）与函数 $y_{2} = k_{2} x$ （ $k_{2}$ 是常数， $k_{2} \neq 0$ ）的图象交于点A，点A关于 $y$ 轴的对称点为点B。

(1)、若点B的坐标为（-1，2），
①求 $k_{1}$ ， $k_{2}$ 的值； ②当 $y_{1} < y_{2}$ 时，直接写出 $x$ 的取值范围；

(2)、若点B在函数 $y_{3} = \frac{k_{3}}{x}$ （ $k_{3}$ 是常数， $k_{3} \neq 0$ ）的图象上，求 $k_{1} + k_{3}$ 的值。

查看试题解析

31. 经过实验获得两个变量x(x>0)，y(y>0)的一组对应值如下表。

x	1	2	3	4	5	6
y	6	2.9	2	1.5	1.2	1

(1)、请画出相应函数的图象，并求出函数表达式。

(2)、点A(x₁ ， y₁)，B(x₂ ， y₂)在此函数图象上。若x₁<x₂ ，则y₁ ， y₂有怎样的大小关系？请说明理由。

查看试题解析

32. 设函数y₁= $\frac{k}{x}$ ，y₂=- $\frac{k}{x}$ (k>0)。

(1)、当2≤x≤3时，函数y₁的最大值是a，函数y₂的最小值是a-4，求a和k的值。

(2)、设m≠0，且m≠-1，当x=m时，y₁=p；当x=m+1时，y₁=q。圆圆说：“p一定大于q”。你认为圆圆的说法正确吗？为什么？

查看试题解析
33. 如图1，在平面直角坐标系xOy中，已知△ABC，∠ABC=90°，顶点A在第一象限，B，C在x轴的正半轴上（C在B的右侧），BC=2，AB=2 $\sqrt{3}$ ，△ADC与△ABC关于AC所在的直线对称．

(1)、当OB=2时，求点D的坐标；

(2)、若点A和点D在同一个反比例函数的图象上，求OB的长；

(3)、如图2，将第（2）题中的四边形ABCD向右平移，记平移后的四边形为A₁B₁C₁D₁ ，过点D₁的反比例函数y= $\frac{k}{x}$ （k≠0）的图象与BA的延长线交于点P．问：在平移过程中，是否存在这样的k，使得以点P，A₁ ， D为顶点的三角形是直角三角形？若存在，请直接写出所有符合题意的k的值；若不存在，请说明理由．

查看试题解析
34. 设一次函数 $y = k x + b$ （ $k ， b$ 是常数， $k \neq 0$ ）的图象过A（1，3），B（-1，-1）

(1)、求该一次函数的表达式；

(2)、若点（2a+2，a²）在该一次函数图象上，求a的值；

(3)、已知点C（x₁ ， y₁），D（x₂ ， y₂）在该一次函数图象上，设m=（x₁-x₂）（y₁-y₂），判断反比例函数 $y = \frac{m + 1}{x}$ 的图象所在的象限，说明理由。

查看试题解析
35. 如图，在平面直角坐标系中，正次边形ABCDEF的对称中心P在反比例函数y= $\frac{k}{x}$ （k＞0，x>0）的图象上，边CD在x轴上，点B在y轴上，已知CD=2．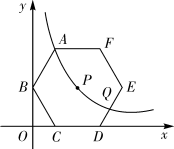

(1)、点A是否在该反比例函数的图象上？请说明理曲。

(2)、若该反比例函数图象与DE交于点Q，求点Q的横坐标。

(3)、平移正六边形ABCDEF，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程。

查看试题解析