浙江省历年（2018-2022年）真题分类汇编专题16 二次函数与一次函数、一元二次方程、不等式的综合应用

试卷更新日期：2022-08-14 类型：二轮复习

进入出卷网下载

一、单选题

1. 已知抛物线 y=x²+mx的对称轴为直线 x=2 ，则关于x的方程 x²+mx=5的根是（）

A、0，4 B、1，5 C、1，－5 D、－1，5

查看试题解析
2. 已知 $y_{1}$ 和 $y_{2}$ 均是以 $x$ 为自变量的函数，当 $x = m$ 时，函数值分别是 $M_{1}^{}$ 和 $M_{2}$ ，若存在实数 $m$ ，使得 $M_{1}^{} + M_{2} = 0$ ，则称函数 $y_{1}$ 和 $y_{2}$ 具有性质P。以下函数 $y_{1}$ 和 $y_{2}$ 具有性质P的是（）

A、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = - x - 1$ B、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = - x + 1$ C、 $y_{1} = - \frac{1}{x}$ 和 $y_{2} = - x - 1$ D、 $y_{1} = - \frac{1}{x}$ 和 $y_{2} = - x + 1$

查看试题解析
3. 在平面直角坐标系中，已知函数y₁=x²+ax+1，y₂=x²+bx+2，y₃=x²+cx+4，其中a，b，c是正实数，且满足b²=ac。设函数y₁ ， y₂ ， y₃的图象与x轴的交点个数分别为M₁ ， M₂ ， M₃ ，（）

A、若M₁=2，M₂=2，则M₃=0 B、若M₁=1，M₂=0，则M₃=0 C、若M₁=0，M₂=2，则M₃=0 D、若M₁=0，M₂=0，则M₃=0

查看试题解析
4. 小飞研究二次函数 $y = - {(x - m)}^{2} - m + 1$ ( $m$ 为常数)性质时如下结论：
①这个函数图象的顶点始终在直线 $y = - x + 1$ 上；②存在一个 $m$ 的值，使得函数图象的顶点与 $x$ 轴的两个交点构成等腰直角三角形；③点 $A (x_{1} ， y_{1})$ 与点 $B (x_{2} ， y_{2})$ 在函数图象上，若 $x_{1} < x_{2}$ ， $x_{1} + x_{2} > 2 m$ ，则 $y_{1} < y_{2}$ ；④当 $- 1 < x < 2$ 时， $y$ 随 $x$ 的增大而增大，则 $m$ 的取值范围为 $m \geq 2$ 其中错误结论的序号是（）

A、① B、② C、③ D、④

查看试题解析
5. 在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y=ax²﹣x+2（a≠0）与线段MN有两个不同的交点，则a的取值范围是（）

A、a≤﹣1或 $\frac{1}{4}$ ≤a＜ $\frac{1}{3}$ B、 $\frac{1}{4}$ ≤a＜ $\frac{1}{3}$ C、a≤ $\frac{1}{4}$ 或a＞ $\frac{1}{3}$ D、a≤﹣1或a≥ $\frac{1}{4}$

查看试题解析

二、作图题

6. 某宾馆有若干间标准房，当标准房的价格为200元时，每天入住的房间数为60间，经市场调查表明，该宾馆每间标准房的价格在170~240元之间（含170元，240元）浮动时，每天入住的房间数y（间）与每间标准房的价格x（元）的数据如下表：

x（元）

…

190

200

210

220

…

y(间)

…

65

60

55

50

…

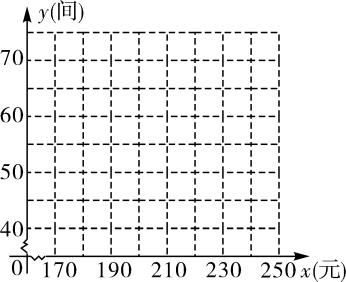(1)、根据所给数据在坐标系中描出相应的点，并画出图象。

(2)、求y关于x的函数表达式、并写出自变量x的取值范围.

(3)、设客房的日营业额为w（元）。若不考虑其他因素，问宾馆标准房的价格定为多少元时。客房的日营业额最大?最大为多少元？

查看试题解析

三、综合题

7. 在直角坐标系中，设函数 $y = a x^{2} + b x + 1$ （ $a$ ， $b$ 是常数， $a \neq 0$ ）。

(1)、若该函数的图象经过（1，0）和（2，1）两点，求函数的表达式，并写出函数图象的顶点坐标；

(2)、写出一组a、b的值，使函数y=ax²+bx+1的图象与x轴有两个不同的交点，并说明理由.

(3)、已知 $a = b = 1$ ，当 $x = p$ ， $q$ （ $p$ ， $q$ 是实数， $p \neq q$ ）时，该函数对应的函数值分别为P，Q。若 $p + q = 2$ ，求证：P+Q>6 。

查看试题解析
8. 已知抛物线 $y = a x^{2} - 2 a x - 8$ $(a \neq 0)$ 经过点 $(- 2 ， 0)$ .

(1)、求抛物线的函数表达式和顶点坐标.

(2)、直线 $l$ 交抛物线于点 $A (- 4 ， m)$ ， $B (n ， 7)$ ， $n$ 为正数.若点 $P$ 在抛物线上且在直线 $l$ 下方（不与点 $A$ ， $B$ 重合），分别求出点 $P$ 横坐标与纵坐标的取值范围，

查看试题解析
9. 如图，已知经过原点的抛物线 $y = 2 x^{2} + m x$ 与x轴交于另一点A（2，0）。

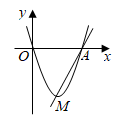(1)、求m的值和抛物线顶点M的坐标；

(2)、求直线AM的解析式。

查看试题解析
10. 在平面直角坐标系中，设二次函数y₁=x²+bx+a，y₂=ax²+bx+1(a，b是实数，a≠0)。

(1)、若函数y₁的对称轴为直线x=3，且函数y₁的图象经过点(a，b)，求函数y₁的表达式。

(2)、若函数y₁的图象经过点(r，0)，其中r≠0，求证：函数y₂的图象经过点( $\frac{1}{r}$ ，0)。

(3)、若函数y₁和函数y₂的最小值分别为m和n，若m+n=0，求m，n的值。

查看试题解析
11. 如图，在平面直角坐标系中，二次函数 $y = - \frac{1}{2} x^{2} + 2 x + 6$ 的图象交x轴于点A，B（点A在点B的左侧）．

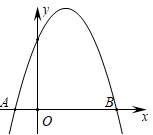(1)、求点A，B的坐标，并根据该函数图象写出y≥0时x的取值范围；

(2)、把点B向上平移m个单位得点B₁ ．若点B₁向左平移n个单位，将与该二次函数图象上的点B₂重合；若点B₁向左平移(n＋6)个单位，将与该二次函数图象上的点B₃重合．已知m＞0，n＞0，求m ， n的值．

查看试题解析
12. 如图，抛物线 $y = a x^{2} + b x (a \neq 0)$ 交 $x$ 轴正半轴于点A，直线 $y = 2 x$ 经过抛物线的顶点M．已知该抛物线的对称轴为直线 $x = 2$ ，交 $x$ 轴于点B．

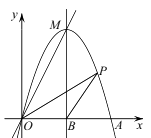(1)、求a，b的值．

(2)、P是第一象限内抛物线上的一点，且在对称轴的右侧，连接OP，BP．设点P的横坐标为 $m$ ，△OBP的面积为S，记 $K = \frac{S}{m}$ ．求K关于 $m$ 的函数表达式及K的范围．

查看试题解析
13. 已知，点M为二次函数y=-（x-b）²＋4b＋1图象的顶点，直线y=mx＋5分别交x轴正半轴，y轴于点A，B。

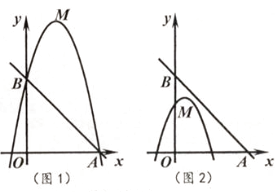(1)、判断顶点M是否在直线y=4x＋1上，并说明理由。

(2)、如图1，若二次函数图象也经过点A，B，且mx＋5＞-（x-b）²＋4b＋1，根据图象，写出x的取值范围。

(3)、如图2，点A坐标为（5，0），点M在△AOB内，若点C（ $\frac{1}{4}$ ，y₁），D（ $\frac{3}{4}$ ，y₂）都在二次函数图象上，试比较y₁与y₂的大小。

查看试题解析
14. 某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为批物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合，如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系。

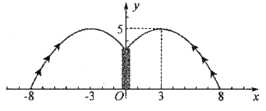(1)、求水柱所在抛物线（第一象限部分）的函数表达式；

(2)、王师傅在水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

(3)、经检修评估，游乐园决定对喷水设施做如下设计改进；在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后水热水柱的最大高度。

查看试题解析
15. 已知抛物纸L₁：y=a(x+1)²-4(a≠0)经过点A(1，0)。

(1)、求抛物线L₁的函数表达式。

(2)、将抛物线L₁向上平移m(m>0)个单位得到抛物线L₂ ，若抛物线L₂的顶点关于坐标原点O的对称点在抛物线L₁上，求m的值．

(3)、把抛物线L₁向右平移n(n>0)个单位得到抛物线L₃ ，已知点P(8-t，s)，Q(t-4，r)都在抛物线L₃上，若当t>6时，都有s>r，求n的取值范围．

查看试题解析

x（元）	…	190	200	210	220	…
y(间)	…	65	60	55	50	…