浙江省历年(2018-2022年)真题分类汇编专题13 函数的概念与图象
试卷更新日期:2022-08-14 类型:二轮复习
一、单选题
-
1. 吴老师家、公园、学校依次在同一条直线上,家到公园、公园到学校的距离分别为 400m, 600m.他从家出发匀速步行8min到公园后,停留 4min,然后匀速步行6min到学校,设吴老师离公园的距离为y(单位: m),所用时间为x (单位: min),则下列表示y与 x之间函数关系的图象中,正确的是( )A、
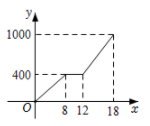 B、
B、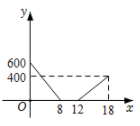 C、
C、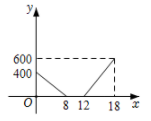 D、
D、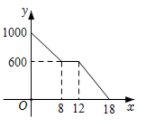 2. 小聪某次从家出发去公园游玩的行程如图所示,他离家的路程为s米,所经过的时间为t分钟,下列选项中的图象,能近似刻画s与t之间关系的是( )
2. 小聪某次从家出发去公园游玩的行程如图所示,他离家的路程为s米,所经过的时间为t分钟,下列选项中的图象,能近似刻画s与t之间关系的是( )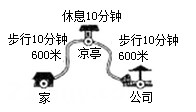 A、
A、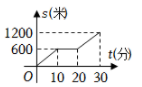 B、
B、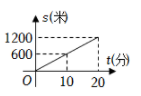 C、
C、 D、
D、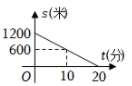 3. 如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v(单位:m/s)与运动时间t (单位:s)的函数图象如图2,则该小球的运动路程y(单位:m)与运动时间t(单位:s)之间的函数图象大致是( )
3. 如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v(单位:m/s)与运动时间t (单位:s)的函数图象如图2,则该小球的运动路程y(单位:m)与运动时间t(单位:s)之间的函数图象大致是( ) A、
A、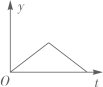 B、
B、 C、
C、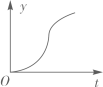 D、
D、 4. 如图,一个函数的图象由射线 、线段 、射线 组成,其中点 , , , ,则此函数( )
4. 如图,一个函数的图象由射线 、线段 、射线 组成,其中点 , , , ,则此函数( )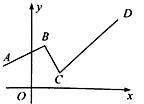 A、当 时, 随 的增大而增大 B、当 时, 随 的增大而减小 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小5. 如图,一个函数的图象由射线BA,线段BC,射线CD组成,其中点A(-1,2),B(1,3),C(2,1),D(6,5),则此函数( )
A、当 时, 随 的增大而增大 B、当 时, 随 的增大而减小 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小5. 如图,一个函数的图象由射线BA,线段BC,射线CD组成,其中点A(-1,2),B(1,3),C(2,1),D(6,5),则此函数( )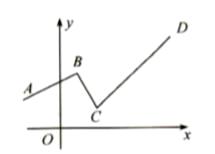 A、当x<1,y随x的增大而增大 B、当x<1,y随x的增大而减小 C、当x>1,y随x的增大而增大 D、当x>1,y随x的增大而减小6. 如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C,设P点经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是( )
A、当x<1,y随x的增大而增大 B、当x<1,y随x的增大而减小 C、当x>1,y随x的增大而增大 D、当x>1,y随x的增大而减小6. 如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C,设P点经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是( )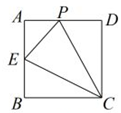 A、
A、 B、
B、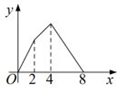 C、
C、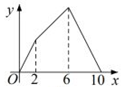 D、
D、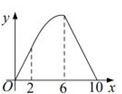
二、填空题
-
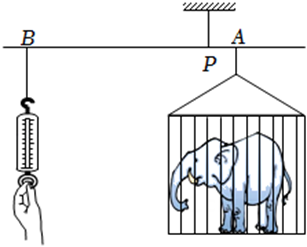
7. 某动物园利用杠杆原理称象:如图,在点P处挂一根质地均匀且足够长的钢梁(呈水平状态),将装有大象的铁笼和弹簧秤(秤的重力忽略不计)分别县挂在钢梁的点A,B处,当钢梁保持水平时,弹簧秤读数为k(N).若铁笼固定不动,移动弹簧秤使BP扩大到原来的n(n>1)倍,且钢梁保持水平,则弹簧秤读数为(N)(用含n,k的代数式表示).
三、综合题
-
8. 6月13日,某港口的湖水高度y(cm)和时间x(h)的部分数据及函数图象如下:
x(h)
…
11
12
13
14
15
16
17
18
…
Y(cm
…
189
137
103
80
101
133
202
260
…
(数据来自某海洋研究所)
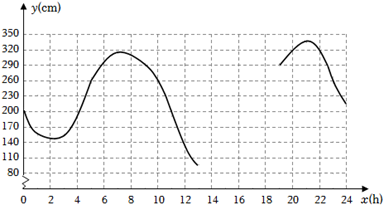 (1)、数学活动:
(1)、数学活动:①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当x=4时,y的值为多少?当y的值最大时,x的值为多少?
(2)、数学思考:请结合函数图象,写出该函数的两条性质或结论.
(3)、数学应用:根据研究,当潮水高度超过260cm时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?
9. 6月13日,某港口的湖水高度y(cm)和时间x(h)的部分数据及函数图象如下:x(b)
……
11
12
13
14
15
16
17
18
……
y(cm)
……
189
137
103
80
101
133
202
260
……
(数据来自某海举研究所)
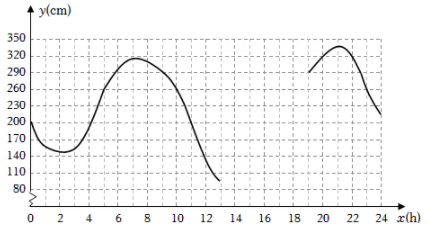 (1)、数学活动:
(1)、数学活动:①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当x=4时,y的值为多少?当y的值最大时,x的值为多少?
(2)、数学思考:请结合函数图象,写出该函数的两条性质或结论.
(3)、数学应用:根据研究,当潮水高度超过260cm时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?
10. 因疫情防控需要,一辆货车先从甲地出发运送防疫物资到乙地,稍后一辆轿车从甲地急送防疫专家到乙地.已知甲、乙两地的路程是330km,货车行驶时的速度是60km/h.两车离甲地的路程s(km)与时间t(h)的函数图象如图.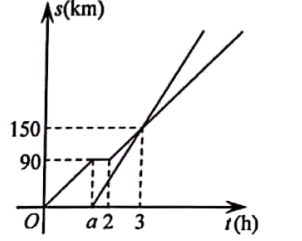 (1)、求出a的值;(2)、求轿车离甲地的路程s(km)与时间t(h)的函数表达式:(3)、问轿车比货车早多少时间到达乙地?11. 根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.
(1)、求出a的值;(2)、求轿车离甲地的路程s(km)与时间t(h)的函数表达式:(3)、问轿车比货车早多少时间到达乙地?11. 根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.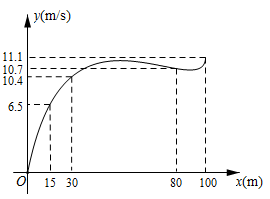 (1)、y是关于x的函数吗?为什么?(2)、“加速期”结束时,小斌的速度为多少?(3)、根据如图提供的信息,给小斌提一条训练建议.12. 小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与动时间t(s)之间的关系如图2所示。
(1)、y是关于x的函数吗?为什么?(2)、“加速期”结束时,小斌的速度为多少?(3)、根据如图提供的信息,给小斌提一条训练建议.12. 小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与动时间t(s)之间的关系如图2所示。 (1)、根据函数的定义,请判断变量h是否为关于t的函数?(2)、结合图象回答:
(1)、根据函数的定义,请判断变量h是否为关于t的函数?(2)、结合图象回答:①当t=0.7s时,h的值是多少?并说明它的实际意义,
②秋千摆动第一个来回需多少时间?
-