浙江省历年（2018-2022年）真题分类汇编专题10 一元二次方程

试卷更新日期：2022-08-14 类型：二轮复习

进入出卷网下载

一、单选题

1. 能说明命题“关于x的方程x²-4x+m=0一定有实数根”是假命题的反例为（）

A、m=-1 B、m=0 C、m=4 D、m=5

查看试题解析
2. 欧几里得的《原本》记载，形如x²＋ax=b²的方程的图解法是；画Rt△ABC，使∠ACB=90°，BC= $\frac{a}{2}$ ，AC=b，再在斜边AB上截取BD= $\frac{a}{2}$ 。则该方程的一个正根是（）

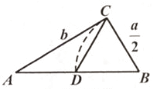A、AC的长 B、AD的长 C、BC的长 D、CD的长

查看试题解析
3. 若关于x的方程x²+6x+c=0有两个相等的实数根，则c的值是（）

A、36 B、-36 C、9 D、-9

查看试题解析
4. 关于x的方程x²﹣4x+m＝0有两个不相等的实数根，则m的取值范围是（）

A、m＞2 B、m＜2 C、m＞4 D、m＜4

查看试题解析
5. 某厂家2020年1~5月份的口罩产量统计如图所示。设从2月份到4月份，该厂家口罩产量的平均月增长率为x，根据题意可得方程（）

A、180（1-x）²=461 B、180（1+x）²=461 C、368（1-x）²=442 D、368（1+x）²=442

查看试题解析
6. 已知关于x的一元二次方程 $x^{2} + b x - 1 = 0$ ，则下列关于该方程根的判断，正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关

查看试题解析
7. 用配方法解方程x²-6x-8=0时，配方结果正确的是（）

A、(x-3)²=17 B、(x-3)²=14 C、（x-6)²=44 D、(x-3）²=1

查看试题解析

二、填空题

8. 已知关于 $x$ 的一元二次方程 $x^{2} + 3 x + m = 0$ 有两个相等的实数根，则 $m =$ ．

查看试题解析
9. 在 $x^{2} + () + 4 = 0$ 的括号中添加一个关于 $x$ 的一次项，使方程有两个相等的实数根

查看试题解析
10. 在x²+ +4=0的括号中添加一个关于x的一次项，使方程有两个相等的实数根。

查看试题解析
11. 某网络学习平台2019年的新注册用户数为100万，2021年的新注册用户数为169万，设新注册用户数的年平均增长率为x（x>0），则x= (用百分数表示)．

查看试题解析

三、计算题

12.

(1)、计算： $2 tan 60 ° - \sqrt{12} - {(\sqrt{3} - 2)}^{0} + {(\frac{1}{3})}^{- 1}$ .

(2)、解方程： $x^{2} - 2 x - 1 = 0$ .

查看试题解析
13.

(1)、计算： $2 \tan 60 ° - \sqrt{12} - {(\sqrt{3} - 2)}^{0} + {(\frac{1}{3})}^{- 1}$

(2)、解方程：x²-2x-1=0

查看试题解析

四、解答题

14. 小敏与小霞两位同学解方程3（x﹣3）＝（x﹣3）²的过程如下框：

小敏：

两边同除以（x﹣3），得

3＝x﹣3，

则x＝6．

小霞：

移项，得3（x﹣3）﹣（x﹣3）²＝0，

提取公因式，得（x﹣3）（3﹣x﹣3）＝0．

则x﹣3＝0或3﹣x﹣3＝0，

解得x₁＝3，x₂＝0．

你认为他们的解法是否正确？若正确请在框内打“√”；若错误请在框内打“×”，并写出你的解答过程．

查看试题解析

五、综合题

15. 温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件获利减少2元．设每天安排 $x$ 人生产乙产品．

(1)、根据信息填表
产品种类
每天工人数（人）
每天产量（件）
每件产品可获利润（元）
甲

15
乙
$x$
$x$

(2)、若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润．

(3)、该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润W（元）的最大值及相应的 $x$ 值．

查看试题解析
16. 设一次函数 $y = k x + b$ （ $k ， b$ 是常数， $k \neq 0$ ）的图象过A（1，3），B（-1，-1）

(1)、求该一次函数的表达式；

(2)、若点（2a+2，a²）在该一次函数图象上，求a的值；

(3)、已知点C（x₁ ， y₁），D（x₂ ， y₂）在该一次函数图象上，设m=（x₁-x₂）（y₁-y₂），判断反比例函数 $y = \frac{m + 1}{x}$ 的图象所在的象限，说明理由。

查看试题解析
17. 如图，在△ABC中，∠ACB=90°，以点B为圆心，BC的长为半径画弧，交线段AB于点D，以点A为圆心，AD长为半径画弧，交线段AC于点E，连结CD。

(1)、若∠A=28°，求∠ACD的度数；

(2)、设BC=a，AC=b；
①线段AD的长度是方程 $x^{2} + 2 a x - b^{2} = 0$ 的一个根吗？说明理由。
②若线段AD=EC，求 $\frac{a}{b}$ 的值．

查看试题解析

18. 今年以来，我市接待的游客人数逐月增加。据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人。

(1)、求四月和五月这两个月中，该景区游客人数平均每月增长百分之几；

(2)、若该景区仅有A，B两个景点，售票处出示的三种购票方式如下表所示：

购票方式	甲	乙	丙
可游玩景点	A	B	A和B
门票价格	100元/人	80元/人	160元/人

据预测，六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万，并且当甲、乙两种门票价格不变时，丙种门票每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票。

①若丙种门票下降10元，求景区六月份的门票总收入；

②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？

查看试题解析

19. 背景：点A在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上， $A B ⊥ x$ 轴于点B， $A C ⊥ y$ 轴于点C，分别在射线 $A C ， B O$ 上取点 $D ， E$ ，使得四边形 $A B E D$ 为正方形.如图1，点A在第一象限内，当 $A C = 4$ 时，小李测得 $C D = 3$ .
探究：通过改变点A的位置，小李发现点D，A的横坐标之间存在函数关系.请帮助小李解决下列问题.

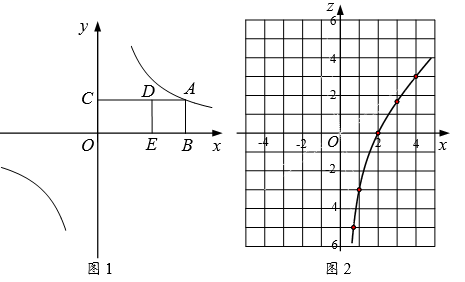(1)、求k的值.

(2)、设点 $A ， D$ 的横坐标分别为 $x ， z$ ，将z关于x的函数称为“Z函数”.如图2，小李画出了 $x > 0$ 时“Z函数”的图象.
①求这个“Z函数”的表达式.

②补画 $x < 0$ 时“Z函数”的图象，并写出这个函数的性质（两条即可）.

③过点 $(3 ， 2)$ 作一直线，与这个“Z函数”图象仅有一个交点，求该交点的横坐标.

查看试题解析

产品种类	每天工人数（人）	每天产量（件）	每件产品可获利润（元）
甲			15
乙	$x$	$x$