2022-2023初数北师大版八年级上册5.5应用二元一次方程组——里程碑上的数同步练习

试卷更新日期：2022-08-14 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 在学习完“垃圾分类”的相关知识后，小明和小丽一起收集了一些废电池，小明说：“我比你多收集了7节废电池啊！”小丽说：“如果你给我8节废电池，我的废电池数量就是你的2倍”．如果他们说的都是真的，设小明收集了x节废电池，小丽收集了y节废电池，则可列方程组为（）．

A、 ${\begin{array}{l} x - y = 7 \\ x - 8 = 2 (y + 8) \end{array}$ B、 ${\begin{array}{l} y - x = 7 \\ x + 8 = 2 (y - 8) \end{array}$ C、 ${\begin{array}{l} x - y = 7 \\ 2 (x - 8) = y \end{array}$ D、 ${\begin{array}{l} x - y = 7 \\ 2 (x - 8) = y + 8 \end{array}$

查看试题解析

2. 爸爸骑摩托车带着小明在公路上匀速行驶，小明每隔一段时间看到的里程碑上的数如下：

时刻	9：00	10：00	11：30
里程碑上的数	是一个两位数，它的两个数字之和是6	是一个两位数，它的十位与个位数字与9：00所看到的正好互换了	是一个三位数，它比9：00时看到的两位数中间多了个0

则10：00时看到里程碑上的数是（）

A、15 B、24 C、42 D、51

查看试题解析

3. 爸爸开车带着小明在公路上匀速行驶，小明每隔一段时间看到的里程碑上的数如下

时刻	9：00	9：45	12：00
碑上的数	是一个两位数，数字之和是9	十位与个位数字与9：00时所看到的正好相反	比9：00时看到的两位数中间多了个0

9：00时看到的两位数是（）

A、54 B、45 C、36 D、27

查看试题解析

4. 某学校体育场的环形跑道长250m，甲、乙分别以一定的速度练习长跑和骑自行车，同时同地出发，如果反向而行，那么他们每隔20s相遇一次．如果同向而行，那么每隔50s乙就追上甲一次，设甲的速度为xm/s，乙的速度为ym/s，则可列方程组为（　　）

A、 ${\begin{array}{l} 20 (x + y) = 250 \\ 50 (y - x) = 250 \end{array}$ B、 ${\begin{array}{l} 20 (y - x) = 250 \\ 50 (x + y) = 250 \end{array}$ C、 ${\begin{array}{l} 20 (x - y) = 500 \\ 50 (x + y) = 250 \end{array}$ D、 ${\begin{array}{l} 20 (x + y) = 250 \\ 50 (y - x) = 500 \end{array}$

查看试题解析
5. 佳佳坐在匀速行驶的车上，将每隔一段时间看到的里程碑上的数描述如下：
时刻
12：00
13：00
14：00
里程碑上的数
是一个两位数，数字之和为7
十位数字和个位数字与12：00时看到的刚好相反
比12：00看到的两位数中间多了个0
则12：00时看到的两位数是（）

A、16 B、25 C、34 D、52

查看试题解析
6. 一个两位数的十位数字与个位数字的和是8，把这个两位数加上18，结果恰好为数字对调后组成的两位数，求这个两位数.设个位数字为x，十位数字为y，则所列方程组正确的是（）

A、 ${\begin{cases} x + y = 8 \\ x y + 18 = y x \end{cases}$ B、 ${\begin{cases} x + y = 8 \\ x + 10 y + 18 = 10 x + y \end{cases}$ C、 ${\begin{cases} x + y = 8 \\ 10 x + y + 18 = y x \end{cases}$ D、 ${\begin{cases} x + y = 8 \\ 10 （ x + y ） = y x \end{cases}$

查看试题解析
7. 甲、乙两个仓库共存粮450吨，现从甲仓库运出存粮的60%，从乙仓库运出存粮的40%，结果乙仓库所剩的粮食比甲仓库所剩的粮食多30吨.若设甲仓库原来存粮x吨，乙仓库原来存粮y吨，则有（）

A、 ${\begin{cases} x + y = 450 \\ （ 1 - 60 % ） x - （ 1 - 40 % ） y = 30 \end{cases}$ B、 ${\begin{cases} x + y = 450 \\ 60 % x - 40 % y = 30 \end{cases}$ C、 ${\begin{cases} x + y = 450 \\ （ 1 - 40 % ） y - （ 1 - 60 % ） x = 30 \end{cases}$ D、 ${\begin{cases} x + y = 450 \\ 40 % y - 60 % x = 30 \end{cases}$

查看试题解析
8. 商店用3000元购进甲乙两种货物，卖出后，甲种货物的利润率是10%，乙种货物的利润率是11%，两种货物共获利315元。设该商店购进这两种货物所用的费用分别为x元，y元，则列出方程组是（）

A、 ${\begin{array}{l} x + y = 3315 \\ x (1 + 10 %) + y (1 + 11 %) = 315 \end{array}$ B、 ${\begin{array}{l} x + y = 3315 \\ 10 % x + 11 % y = 315 \end{array}$ C、 ${\begin{array}{l} x + y = 3000 \\ x (1 + 10 %) + y (1 + 11 %) = 315 \end{array}$ D、 ${\begin{array}{l} x + y = 3000 \\ 10 % x + 11 % y = 315 \end{array}$

查看试题解析
9. 如图，分别用火柴棍连续搭建等边三角形和正六边形，公共边只用一根火柴棍.如果搭建等边三角形和正六边形共用了2018根火柴，并且等边三角形的个数比正六边形的个数多7，那么连续搭建的等边三角形的个数是（　　）

A、291 B、292 C、293 D、294

查看试题解析
10. 某公司上半年生产甲，乙两种型号的无人机若干架.已知甲种型号无人机架数比总架数的一半多11架，乙种型号无人机架数比总架数的三分之一少2架.设甲种型号无人机 $x$ 架，乙种型号无人机 $y$ 架.根据题意可列出的方程组是（）

A、 ${\begin{array}{l} x = \frac{1}{3} (x + y) - 11 ， \\ y = \frac{1}{2} (x + y) + 2 \end{array}$ B、 ${\begin{array}{l} x = \frac{1}{3} (x + y) + 11. \\ y = \frac{1}{2} (x + y) - 2 \end{array}$ C、 ${\begin{array}{l} x = \frac{1}{2} (x + y) - 11 ， \\ y = \frac{1}{3} (x + y) + 2 \end{array}$ D、 ${\begin{array}{l} x = \frac{1}{2} (x + y) + 11 ， \\ y = \frac{1}{3} (x + y) - 2 \end{array}$

查看试题解析

二、填空题（每空2分，共14分）

11. 若素数p，使得 $4 p^{2} + p + 81$ 是一个完全平方数，则p=.（若一个数能表示成某个整数的平方的形式，则称这个数为完全平方数.）

查看试题解析
12. 某出租车起步价所包含的路程为 $0 \sim 2 k m$ ，超过 $2 k m$ 的部分按每千米另收费.小江乘坐这种出租车走了 $7 k m$ ，付了16元；小北乘坐这种出租车走了 $13 k m$ ，付了28元.设这种出租车的起步价为 $x$ 元，超过 $2 k m$ 后每千米收费 $y$ 元.根据题意，可列方程组为.

查看试题解析
13. 今年4月23号，位于重庆两江新区的光环购物公园隆重开业。该购物公园最具吸引力的就是建跨7层，拥有42米立体垂直景观的“沐光森林”植物园.假设该植物园拥有6个出入口，每个出入口都是单向的且在单位时间内每个入口和出口经过的游客数量是一定的；并且植物园的最大承载游客数量也是固定的.由于疫情防控和现场安全的原因，目前植物园对外开放最大可承载游客量为设计数量的90％.假设植物园每天早上九点开始接待游客，若开放5个入口，1个出口，2个小时游客数量就将饱和；若开放3个入口，3个出口，4个小时游客数量将达到饱和.开业当天由于人流量激增，为了安全起见仅开放了2个入口，4个出口，且开业当天游客最大承载量定为总设计可承载人数的84％.请问从早上9点开始，经过小时植物园游客数量达到饱和.

查看试题解析

三、综合题（共7题，共58分）

14. 一次越野赛跑中，当小明跑了 $1600 m$ 时，小刚跑了 $1450 m$ ．此后两人分别以 $a m / s$ 和 $b m / s$ 匀速跑．又过 $100 s$ 时小刚追上小明， $200 s$ 时小刚到达终点， $300 s$ 时小明到达终点，这次越野赛跑的全程为多少米？

查看试题解析
15. 如图，已知点A、点B在数轴上表示的数分别是-20、64，动点M从点A出发，以每秒若干个单位长度的速度向右匀速运动，动点N从点B出发，以每秒若干个单位长度的速度向左匀速运动．若点M、N同时出发，则出发后12秒相遇；若点N先出发7秒，则点M出发10秒后与点N相遇．动点M、N运动的速度分别是多少？

查看试题解析
16. 有一个两位数，设它的十位数字为 $x$ ，个位数字为 $y$ ，已知十位数字与个位数字之和为8，把十位数字和个位数字互换位置后得到一个新的两位数，新的两位数比原来的两位数大18.

(1)、原来的两位数为，新的两位数为.（用含有 $x$ 、 $y$ 的代数式表示）

(2)、根据题意，列出二元一次方程组为.

(3)、求原来的两位数.

查看试题解析
17. $5 G$ 时代的到来将给人类生活带来巨大改变.现有 $A ， B$ 两种型号的 $5 G$ 手机，进价和售价如下表所示：
进价（元/部）
售价（元/部）
$A$
3000
3400
$B$
3500
4000
某营业厅购进 $A ， B$ 两种型号手机共花费32000元.手机销售完成后共获得利润4400元.

(1)、营业厅购进 $A ， B$ 两种型号手机各多少部？

(2)、若营业厅再次购进 $A ， B$ 两种型号手机共30部，其中 $B$ 型手机的数量不多于 $A$ 型手机数量的2倍，请设计一个方案：营业厅购进两种型号手机各多少部时获得最大利润，最大利润是多少？

查看试题解析
18. 甲地到乙地全程5.5km，小明从甲地走路去乙地，其中有一段上坡路、一段平路和一段下坡路.如果上坡路的平均速度为2km/h，下坡路的平均速度为5km/h.

(1)、若小明走路从甲地到乙地需 $\frac{7}{4}$ 小时，从乙地走路到甲地需 $\frac{19}{10}$ 小时，来回走平路分别都用了 $\frac{1}{4}$ 小时，求出小明从甲地到乙地的上坡路和下坡路的路程（请用方程组的方法解）.

(2)、若小明从甲地到乙地，平路上的平均速度为v（km/h），上坡和下坡走的路程分别为1.5km和2km.若小明从乙地到甲地所用的时间与从甲地到乙地的时间相同，求小明从乙地到甲地平路上走的平均速度（用含v的代数式表示）.

查看试题解析
19. 某工厂将一批纸板按甲，乙两种方式进行加工，再用加工出来的长方形 $A$ 板块和正方形 $B$ 板块制作成如图所示的底面为正方形的长方体有盖礼盒. 设x块纸板按甲方式进行加工，y块纸板按乙方式进行加工.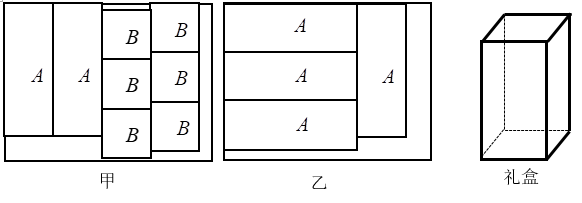

(1)、补全表格.

x块甲方式加工的纸板

y块乙方式加工的纸板

$A$ 板块

2x

$B$ 板块

\

(2)、若现共有纸板14块，要使礼盒制作完毕后的 $A$ ， $B$ 板块恰好用完，能做多少个礼盒？

(3)、若现有 $B$ 板块4块，纸板a块，要使礼盒制作完毕后的 $A$ ， $B$ 板块恰好用完，则a的最小值为. (请直接写出答案)

查看试题解析

20. 水是生命之源，“节约用水，人人有责”.为了加强公民的节水意识，合理利用水资源，某市居民生活用水按阶梯式水价计费，下表是该市居民“一户一表”生活用水及阶梯计费价格表的部分信息（注：水费按月份结算，m³表示立方米）

每户每月用水量（m³）	自来水销售价格（元/m³）	污水处理价格（元/m³）
不超出6m³部分	$a$	1.10
超出6m³不超出10m³的部分	$b$	1.10
超出10m³的部分	7.00	1.10

（注：①每户产生的污水量等于该户自来水用水量；②水费=自来水费用+污水处理费用）.

已知2021年三月份，小红家用水7m³ ，交水费27.2元，小聪家用水9m³ ，交水费38.4元.

(1)、请你根据以上信息，求表中

a

，

b

的值；

(2)、由于七月份正值夏天，小红家预计用水12.5吨，求小红家七月份预计应缴水费多少元？

(3)、若小聪家四、五月份共用水20m³ ，其中四月份的用水量低于五月份的用水量，共缴水费89元，则小聪家四、五月份的用水量各是多少？

查看试题解析

时刻	12：00	13：00	14：00
里程碑上的数	是一个两位数，数字之和为7	十位数字和个位数字与12：00时看到的刚好相反	比12：00看到的两位数中间多了个0

	进价（元/部）	售价（元/部）
$A$	3000	3400
$B$	3500	4000

	x块甲方式加工的纸板	y块乙方式加工的纸板
$A$ 板块	2x
$B$ 板块		\

2022-2023初数北师大版八年级上册5.5应用二元一次方程组——里程碑上的数 同步练习

一、单选题（每题3分，共30分）

二、填空题（每空2分，共14分）

三、综合题（共7题，共58分）

2022-2023初数北师大版八年级上册5.5应用二元一次方程组——里程碑上的数同步练习