高中数学人教A版(2019)选择性必修一 第一章 第四节 空间向量的应用(二)
试卷更新日期:2022-08-13 类型:同步测试
一、单选题
-
1. 如图,已知一个八面体的各条棱长均为2,四边形为正方形,则下列结论正确的是( )
 A、该八面体的体积为 B、该八面体的外接球的表面积为16π C、到平面的距离为 D、与所成角为2. 如图,在三棱锥中,平面ABC, , , , 则点A到平面PBC的距离为( ).
A、该八面体的体积为 B、该八面体的外接球的表面积为16π C、到平面的距离为 D、与所成角为2. 如图,在三棱锥中,平面ABC, , , , 则点A到平面PBC的距离为( ). A、 B、 C、3 D、3. 如图,在直三棱柱中, , , 是的中点,则直线与平面所成角的正弦值为( )
A、 B、 C、3 D、3. 如图,在直三棱柱中, , , 是的中点,则直线与平面所成角的正弦值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
4. 在正方体中,M是的中点,点N在该正方体的棱上运动,则下列说法正确的是( )A、当N为棱中点时, B、当N为棱中点时,MN与平面所成角为30° C、有且仅有三个点N,使得平面 D、有且仅有四个点N,使得MN与所成角为60°5. 已知正方体的棱长为1,则( )A、 B、平面 C、三棱锥的体积为 D、点到直线的距离为
三、解答题
-
6. 如图,在多面体中,平面平面 , 四边形为菱形, , 底面为直角梯形,为的中点.
 (1)、证明:.(2)、若多面体的体积为 , 求点到平面的距离.7. 如图,是半球的直径,为球心,依次是半圆上的两个三等分点,是半球面上一点,且 ,
(1)、证明:.(2)、若多面体的体积为 , 求点到平面的距离.7. 如图,是半球的直径,为球心,依次是半圆上的两个三等分点,是半球面上一点,且 , (1)、证明:平面平面;(2)、若点在底面圆内的射影恰在上,求二面角的余弦值.8. 如图,在圆柱中,是圆的直径,和分别是圆柱轴截面上的母线.
(1)、证明:平面平面;(2)、若点在底面圆内的射影恰在上,求二面角的余弦值.8. 如图,在圆柱中,是圆的直径,和分别是圆柱轴截面上的母线. (1)、证明:平面;(2)、若 , , 证明平面 , 并求点到平面的距离.9. 如图,在四棱锥中,底面 , , , , , 为棱的中点,是线段上一动点.
(1)、证明:平面;(2)、若 , , 证明平面 , 并求点到平面的距离.9. 如图,在四棱锥中,底面 , , , , , 为棱的中点,是线段上一动点. (1)、求证:平面平面;(2)、若直线与平面所成角的正弦值为时,求二面角的余弦值.10. 如图,在四棱锥 中,底面ABCD为等腰梯形, , , 面ABCD, ,点F为线段SD中点
(1)、求证:平面平面;(2)、若直线与平面所成角的正弦值为时,求二面角的余弦值.10. 如图,在四棱锥 中,底面ABCD为等腰梯形, , , 面ABCD, ,点F为线段SD中点 (1)、求证: 面SAB;(2)、求异面直线FC与BD所成角的大小.11. 如图,在四棱柱中,底面为菱形,平面 , 且 , .
(1)、求证: 面SAB;(2)、求异面直线FC与BD所成角的大小.11. 如图,在四棱柱中,底面为菱形,平面 , 且 , .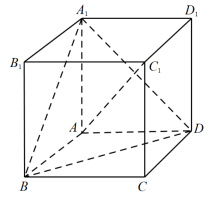 (1)、求点到平面的距离;(2)、①求二面角大小.
(1)、求点到平面的距离;(2)、①求二面角大小.②求直线与平面所成角的大小.
12. 如图,在四棱锥中,底面为平行四边形, , 丄平面 , 且 , , 点是的中点. (1)、求证:平面;(2)、求直线与平面所成角的正弦值.13. 如图,在四棱锥中,平面ABCD,M,N分别为PB,PD的中点,底面ABCD为正方形,且 .
(1)、求证:平面;(2)、求直线与平面所成角的正弦值.13. 如图,在四棱锥中,平面ABCD,M,N分别为PB,PD的中点,底面ABCD为正方形,且 . (1)、若 , 证明:平面AMN.(2)、若平面MNA与底面ABCD所成锐二面角的大小为45°,求PC的长.14. 已知在正方体中,E,F,G分别是棱的中点.
(1)、若 , 证明:平面AMN.(2)、若平面MNA与底面ABCD所成锐二面角的大小为45°,求PC的长.14. 已知在正方体中,E,F,G分别是棱的中点. (1)、证明:与平面不平行;(2)、求直线与平面所成角的正弦值.15. 在四棱锥中,四边形为菱形, , 且平面平面.
(1)、证明:与平面不平行;(2)、求直线与平面所成角的正弦值.15. 在四棱锥中,四边形为菱形, , 且平面平面. (1)、证明:平面;(2)、若为的中点,求直线与平面所成角的正弦值.
(1)、证明:平面;(2)、若为的中点,求直线与平面所成角的正弦值.


