高中数学人教A版(2019)选择性必修一第一章第一节空间向量及其运算(二)
试卷更新日期:2022-08-12 类型:同步测试
一、单选题
-
1. 给出下列命题:
①若将空间中所有的单位向量的起点移到同一个点,则它们的终点构成一个圆;②若空间向量 , 满足 ,则 ;③若空间向量 , , 满足 , ,则 ;④空间中任意两个单位向量必相等;⑤零向量没有方向.
其中假命题的个数是( ).
A、1 B、2 C、3 D、42. 如图所示,在平行六面体 中, 与 的交点为M.设 ,则下列向量中与 相等的向量是( ) A、 B、 C、 D、3. 下列说法正确的是( )A、若 ,则 或 B、若 、 为相反向量,则 C、零向量是没有方向的向量 D、若 、 是两个单位向量,则4. 在三棱柱ABC﹣A1B1C1中,D是CC1的中点,F是A1B的中点,且 ,则( )
A、 B、 C、 D、3. 下列说法正确的是( )A、若 ,则 或 B、若 、 为相反向量,则 C、零向量是没有方向的向量 D、若 、 是两个单位向量,则4. 在三棱柱ABC﹣A1B1C1中,D是CC1的中点,F是A1B的中点,且 ,则( ) A、 B、 C、 D、5. 如图,在空间四边形 中,点 为 中点,点 在 上,且 , 则 等于( )
A、 B、 C、 D、5. 如图,在空间四边形 中,点 为 中点,点 在 上,且 , 则 等于( ) A、 B、 C、 D、6. 空间四边形 中, , , ,点 在 上,且 , 为 中点,则 =( )
A、 B、 C、 D、6. 空间四边形 中, , , ,点 在 上,且 , 为 中点,则 =( )
A、 B、 C、 D、7. 如图:在平行六面体 中, 为 的交点.若 , , ,则向量 ( ) A、 B、 C、 D、8. 如图,在三棱锥 中 ,点D是棱AC的中点 ,若 , , ,则 等于( )
A、 B、 C、 D、8. 如图,在三棱锥 中 ,点D是棱AC的中点 ,若 , , ,则 等于( ) A、 B、 C、 D、9. 在三棱锥 中, 是 的中点,且 ,则 ( )A、 B、 C、 D、10. 如图,在底面 为平行四边形的四棱柱 中,M是AC与BD的交点,若 , , ,则下列向量中与 相等的向量是 ( )
A、 B、 C、 D、9. 在三棱锥 中, 是 的中点,且 ,则 ( )A、 B、 C、 D、10. 如图,在底面 为平行四边形的四棱柱 中,M是AC与BD的交点,若 , , ,则下列向量中与 相等的向量是 ( )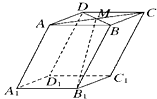 A、 B、 C、 D、11. 在四棱锥P-ABCD中,底面ABCD是正方形,E为PD的中点,若 ,,则 ( )
A、 B、 C、 D、11. 在四棱锥P-ABCD中,底面ABCD是正方形,E为PD的中点,若 ,,则 ( ) A、 B、 C、 D、12. 已知空间四边形OABC, ,N分别是OA,BC的中点,且 , , =c,用a,b,c表示向量 为( )
A、 B、 C、 D、12. 已知空间四边形OABC, ,N分别是OA,BC的中点,且 , , =c,用a,b,c表示向量 为( )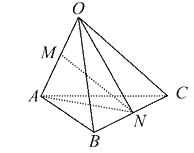 A、 B、 C、 D、
A、 B、 C、 D、二、填空题


