高中数学人教A版(2019)选择性必修一第一章第一节空间向量及其运算(一)
试卷更新日期:2022-08-12 类型:同步测试
一、单选题
-
1. 如图,在三棱锥 中,E为OA的中点,点F在BC上,满足 ,记 , , 分别为 , , ,则 ( )
 A、 B、 C、 D、2. 在三棱锥中,P为内一点,若 , , , 则( )A、 B、 C、 D、3. 如图,在四面体中, , , , 点M、N分别在线段OA、BC上,且 , , 则等于( )
A、 B、 C、 D、2. 在三棱锥中,P为内一点,若 , , , 则( )A、 B、 C、 D、3. 如图,在四面体中, , , , 点M、N分别在线段OA、BC上,且 , , 则等于( ) A、 B、 C、 D、4. 如图,四面体 - , 是底面△ 的重心, ,则 ( )
A、 B、 C、 D、4. 如图,四面体 - , 是底面△ 的重心, ,则 ( )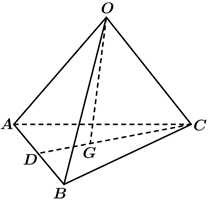 A、 B、 C、 D、5. 若 构成空间的一组基底,则下列向量不共面的是( )A、 , , B、 , , C、 , , D、 , ,6. 在长方体 中,可以作为空间向量一个基底的是( )A、 , , B、 , , C、 , , D、 , ,7. 已知空间任意一点O和不共线三点A,B,C,若 =2 ,则下列结论正确的是( )A、 +2 -2 B、 =-2 +3 C、 =2 -3 D、 =2 -28. 若向量 、 、 的起点与终点 、 、 、 互不重合且无三点共线,且满足下列关系( 是空间任一点),则能使向量 、 、 成为空间一组基底的关系是( )A、 B、 C、 D、9. 在正方体 中,下列各式的运算结果为向量 的是( )
A、 B、 C、 D、5. 若 构成空间的一组基底,则下列向量不共面的是( )A、 , , B、 , , C、 , , D、 , ,6. 在长方体 中,可以作为空间向量一个基底的是( )A、 , , B、 , , C、 , , D、 , ,7. 已知空间任意一点O和不共线三点A,B,C,若 =2 ,则下列结论正确的是( )A、 +2 -2 B、 =-2 +3 C、 =2 -3 D、 =2 -28. 若向量 、 、 的起点与终点 、 、 、 互不重合且无三点共线,且满足下列关系( 是空间任一点),则能使向量 、 、 成为空间一组基底的关系是( )A、 B、 C、 D、9. 在正方体 中,下列各式的运算结果为向量 的是( )① ;② ;③ ;④ .
A、①② B、②③ C、③④ D、①④10. 空间任意四个点A、B、C、D,则 等于 ( )A、 B、 C、 D、11. 若 为空间的一组基底,则下列各项中能构成基底的一组向量是( )A、 B、 C、 D、12. 式子 化简结果是( )A、 B、 C、 D、13. 在三棱柱 中,若 , , ,则A、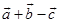 B、
B、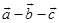 C、
C、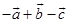 D、
D、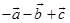
二、多选题
-
14. 已知正方体 ,则下列各式运算结果是 的为( ).A、 B、 C、 D、
三、填空题
-
15. 下列关于空间向量的命题中,
①若向量 , 与空间任意向量都不能构成基底,则 ;
②若非零向量 , , 满足 , ,则有 ;
③若 , , 是空间的一组基底,且 ,则 , , , 四点共面;
④若向量 , , ,是空间一组基底,则 , , 也是空间的一组基底.
上述命题中,正确的有 .
-
