浙江省台州市仙居县2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-11 类型：期末考试

进入出卷网下载

一、选择题

1. 4的算术平方根是（）

A、-2 B、2 C、 $\pm 2$ D、 $\sqrt{2}$

查看试题解析
2. 下列调查中，适合采用全面调查方式的是（）

A、调查我县一饮用水库的水质情况 B、调查某批次汽车的抗撞击能力 C、调查台州市七年级学生的睡眠时间 D、调查某小区新冠肺炎确诊人数

查看试题解析
3. 如图，在平面直角坐标系中，点P的坐标可能是（）

A、 $(1 ， 1)$ B、 $(- 1 ， 1)$ C、 $(- 1 ， - 1)$ D、 $(1 ， - 1)$

查看试题解析
4. 如图，直线a，b被直线c所截，下列条件中，不能得到 $a ∥ b$ 的是（）

A、∠1＝∠3 B、∠2＝∠4 C、∠3＋∠4＝180° D、∠1＋∠4＝180°

查看试题解析
5. 台风是一种破坏性极大的自然灾害，气象台为了预报台风，首先应确定台风中心的位置．下列表述能确定台风中心位置的是（）

A、在沿海地区 B、台湾省以东的洋面上 C、距离台州200km D、北纬28°，东经120°

查看试题解析
6. $x = - 2$ 是下列哪个不等式的一个解（）

A、 $x + 2 > 0$ B、 $2 x \geq 4$ C、 $2 - x < 0$ D、 $x - 2 < 0$

查看试题解析
7. 下列命题是真命题的是（）

A、带根号的数是无理数 B、若 $a > b$ ，则 $a + 2 > b + 1$ C、同旁内角互补 D、相等的角是对顶角

查看试题解析
8. 用含盐16%的甲种盐水和含盐25%的乙种盐水，配制成含盐20%的盐水36kg，则需甲种盐水（）kg.

A、20 B、16 C、26 D、10

查看试题解析
9. 小明在做一道数学题．直线AB，CD相交于点O，∠BOC＝25°，过点O作 $O E ⊥ C D$ ，求∠AOE的度数．小明得到 $∠ A O E = 65 °$ ，但老师说他少了一个答案．那么∠AOE的另一个值是（）

A、105° B、115° C、125° D、135°

查看试题解析
10. 已知a，b满足 $3 a + 2 b = a + b + 3$ ，当 $0 \leq a < 2$ 时，则整数b有（）个.

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 为了考察某校七年级400名学生的视力情况，抽取了80名学生的视力进行调查，那么在这次抽样调查中，样本容量是．

查看试题解析
12. 与 $\sqrt{5}$ 最接近的整数是．

查看试题解析
13. 已知 $x < y$ ，请写出一个实数a，使得 $a x > a y$ ．你所写的实数a是．

查看试题解析
14. 如图，小华同学的家在点P处，他想尽快到公路边，所以选择沿线段PC去公路边，那么他的这一选择体现的数学基本事实是．

查看试题解析
15. 如图，在平面直角坐标系中，点 $A (1 ， 1)$ ，点 $B (3 ， 0)$ ．现将线段AB平移，使点A，B分别平移到点 $A^{'}$ ， $B^{'}$ ，其中点 $A^{'} (1 ， 4)$ ，则四边形 $A A^{'} B^{'} B$ 的面积为．

查看试题解析
16. 杨梅的进价是每千克18元，销售中估计有10%的杨梅正常损耗．为了避免亏本，商家把售价至少定为元/千克．

查看试题解析
17. 已知关于x，y 的二元一次方程组 ${\begin{array}{l} 2 x + 3 y = k \\ x + 2 y = - 1 \end{array}$ 的解互为相反数，则k的值是．

查看试题解析
18. 如图， $A B ∥ C D$ ， $∠ A B C = 40 °$ ， $∠ A C B = 30 °$ ，在直线CD上取点E，使得 $∠ C A E = ∠ A C B$ ，则 $∠ A E C$ 的度数是．

查看试题解析

三、解答题

19. 计算

(1)、 $\sqrt{16} + \sqrt[3]{8} - \sqrt{9}$ ；

(2)、 $3 \sqrt{2} + | \sqrt{3} - \sqrt{2} |$ ．

查看试题解析
20. 解不等式组 ${\begin{array}{l} 3 x - 1 \geq x - 3 \\ \frac{x + 6}{2} > 2 x \end{array}$ ，并在数轴上表示解集．

查看试题解析
21. 解方程组 ${\begin{matrix} x - 3 y = 8 ① \\ 4 x - 3 y = 5 ② \end{matrix}$ 时，两位同学的解法如下：
解法一：由①﹣②，得3x＝3；

解法二：由②得3x+（x﹣3y）③；

把①代入③得3x+8＝5．

(1)、上述两种消元过程是否正确？你的判定是．

A、都正确 B、解法一错 C、解法二错 D、两种都错

(2)、请选择一种你喜欢的方法解此方程组．

查看试题解析
22. 数学课上，老师要求同学们利用三角尺画两条平行线．

(1)、如图1，小颖用两个含30°的三角尺画出平行线a，b．那么小颖得到 $a ∥ b$ 的直接依据是．

(2)、同桌小亮用一个含45°的三角尺和两个含30°的三角尺按如图2方式摆放，并画出平行线a，b．
请帮助小亮完成下面的证明：

由题意得∠ABC＝90°，∠1＝30°，∠2＝60°，过点B作 $B D ∥ a$ ，

又∵∠2＝60°（已知），∴▲ ＝∠2＝60°（）．

∵∠ABC＝90°（已知），∴∠CBD＝ ▲ °．

又∵∠1＝30°（已知），∴∠CBD＝∠1（等量代换），

∴▲ $∥$ ▲ （内错角相等，两直线平行）．

∵ $B D ∥ a$ ，∴ $a ∥ b$ （）．

查看试题解析

23. 某校响应国家号召，为防疫做贡献，决定在全校范围内开展防疫知识的宣传教育活动．为了了解宣传效果，该校在活动前和活动后抽取同一部分学生，就防疫知识进行两次跟踪测评（测试满分100分），两次测评中所有同学的成绩没有低于30分．现在将收集的数据制成频数分布直方图（每一组包含左端值，不包含右端值）和频数分布表．

宣传活动后防疫知识情况统计表

成绩	$30 \leq x < 40$	$40 \leq x < 50$	$50 \leq x < 60$	$60 \leq x < 70$	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x \leq 100$
频数	2	6	6	16	m	30	12

(1)、宣传活动前，在抽取的学生中哪一组成绩的人数最多？占抽取人数的百分之几？

(2)、宣传活动后，在抽取的学生中分数高于65分的至少有人，至多有人；

(3)、小红认为，宣传活动后成绩在60~70的人数为16，比活动前减少了14人，因此学校开展的宣传活动没有效果请你结合统计图表，说一说小红的看法是否正确．

查看试题解析

24. 某学校开设劳动实践课程，各班在同一农具店购买了大锄头和小锄头．七（1）班购买3把大锄头和4把小锄头一共付了180元，七（2）班购买5把大锄头和2把小锄头一共付了230元．

(1)、请问大锄头和小锄头每把各多少元？

(2)、学校准备购买同样的大锄头和小锄头共55把，并要求购买大锄头的费用不低于购买小锄头的费用，问最少需要购买多少把大锄头？

查看试题解析
25. 如图1，有一张四边形ABCD纸片， $A D ∥ B C$ ，点E，F分别在AD，BC上，把纸片沿EF折叠，点D，C分别与点G，H重合，FH交线段AD于点P．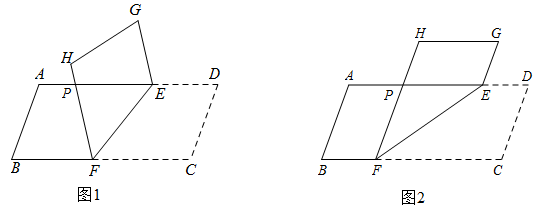

(1)、求证：∠GEA＝∠HFB；

(2)、如图2，∠D＝70°，猜想当∠EFC多少度时， $G H ∥ A D$ ，并说明理由．

查看试题解析
26. 阅读下列材料，解答提出的问题．
我们知道，二元一次方程 $x + y = 1$ 有无数组解，如果我们把每一组解用有序数对 $(x ， y)$ 表示，就可以标出一些以方程 $x + y = 1$ 的解为坐标的点，过这些点中的任意两点可以作一条直线，发现其它点也都在这条直线上．反之，在这条直线上任意取一点，发现这个点的坐标是方程 $x + y = 1$ 的解．我们把以方程 $x + y = 1$ 的解为坐标的所有点组成的图形叫做方程 $x + y = 1$ 的图象，记作直线 $l_{1}$ ．

(1)、【初步探究】下列点中，在方程 $x + y = 1$ 的图象 $l_{1}$ 上的是______；

A、 $(1 ， 1)$ B、 $(2 ， - 1)$ C、 $(- 3 ， 2)$

(2)、在所给的坐标系中画出方程 $x - 2 y = - 3$ 的图象 $l_{2}$ ；

(3)、【理解应用】直线 $l_{1}$ ， $l_{2}$ 相交于点M，求点M的坐标；

(4)、点 $P (x_{1} ， a)$ ， $Q (x_{2} ， a)$ 分别在直线 $l_{1}$ ， $l_{2}$ 上．当 $P Q \leq 4$ 时，请直接写出a的取值范围．

查看试题解析