浙江省宁波市海曙区部分校2021-2022学年七年级下学期期末联考数学试卷
试卷更新日期:2022-08-11 类型:期末考试
一、选择题(本大题共10小题,共30分)
-
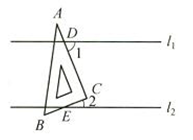
1. 细菌的个体十分微小,大约10亿个细菌堆积起来才有一颗小米粒那么大,某种细菌的直径是0.0000025米,用科学记数法表示这种细菌的直径是( )A、 米 B、 米 C、 米 D、 米2. 下列计算正确的是( )A、a6+a6=a12 B、a6×a2=a8 C、a6÷a2=a3 D、(a6)2=a83. 下列调查适用抽样调查的是( )A、了解全国人民对垃圾分类的赞同情况 B、某单位职工健康检查 C、疫情期间,对某校到校学生进行体温检测 D、检测长征火箭的零件质量4. 下列说法错误的是( )A、对顶角相等 B、同位角相等 C、同角的余角相等 D、同角的补角相等5. 如图,直线 ,一直角三角板 ( )放在平行线上,两直角边分别与 、 交于点D、E,现测得 ,则 的度数为( )
 A、35° B、30° C、25° D、15°6. 若 是方程 的一个解,则a的值为( )A、1 B、-1 C、7 D、-77. 下列各数中,不能整除 的是( )A、78 B、79 C、80 D、818. 若代数式 通过变形可以写成 的形式,则m的值是( )A、5 B、10 C、±5 D、±109. 《九章算术》是中国传统数学的重要著作,书中有一道题“今有五雀六燕,集称之衡,雀俱重,燕俱轻;一雀一燕交而处,衡适平;并燕雀重一斤问:燕雀一枚,各重几何?”译文:“五只雀、六只燕,共重1斤(古时1斤=16两).雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕重量各为多少?”设雀重x两,燕重y两,可列出方程组( )A、 B、 C、 D、10. 已知关于x,y的方程组 的解是 ,则方程组 的解是( )A、 B、 C、 D、
A、35° B、30° C、25° D、15°6. 若 是方程 的一个解,则a的值为( )A、1 B、-1 C、7 D、-77. 下列各数中,不能整除 的是( )A、78 B、79 C、80 D、818. 若代数式 通过变形可以写成 的形式,则m的值是( )A、5 B、10 C、±5 D、±109. 《九章算术》是中国传统数学的重要著作,书中有一道题“今有五雀六燕,集称之衡,雀俱重,燕俱轻;一雀一燕交而处,衡适平;并燕雀重一斤问:燕雀一枚,各重几何?”译文:“五只雀、六只燕,共重1斤(古时1斤=16两).雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕重量各为多少?”设雀重x两,燕重y两,可列出方程组( )A、 B、 C、 D、10. 已知关于x,y的方程组 的解是 ,则方程组 的解是( )A、 B、 C、 D、二、填空题(本大题共8小题,共24分)
-
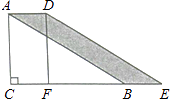
11. 计算 .12. 分解因式: .13. 若分式 没有意义,则x的值是.14. 已知 , ,则 的值为.15. 一组数共含有40个,把它分成5组,若第2,3,4组的频数之和为28,第1组的频率为0.2,则第5组的频数是.16. 如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB向右平移得到△DEF,若平移距离为2,则四边形ABED的面积等于 .
 17. 将一条两边沿互相平行的纸带按如图折叠,若 ,则 .
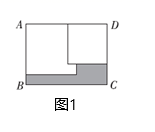
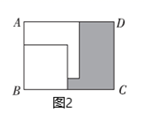
17. 将一条两边沿互相平行的纸带按如图折叠,若 ,则 .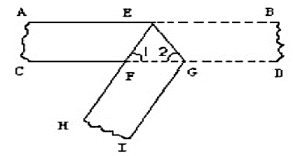 18. 已知长方形 , , ,将两张边长分别为a和b( )的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1 , 图2中阴影部分的面积为S2 . 当 时,AB= .
18. 已知长方形 , , ,将两张边长分别为a和b( )的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1 , 图2中阴影部分的面积为S2 . 当 时,AB= .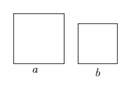
三、解答题(本大题共6小题,共46分)
-
19. 解方程(组):(1)、(2)、20. 学生对小区居民的健身方式进行调查,并将调查结果绘制成如图所示的两幅不完整的统计图.请根据所给信息解答下列问题:
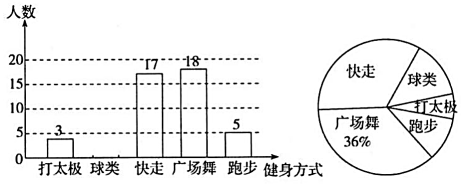 (1)、本次共调查了人;(2)、补全条形统计图,扇形统计图中“跑步”所对应的扇形的圆心角的度数是 ▲ ;(3)、估计小区居民2000人中喜欢打太极的有多少人.21. 先化简,再求值: ,其中, , .22. 根据疫情防控工作需要,某社区组织甲、乙两支医疗队开展疫苗接种工作,甲队比乙队每小时多接种30人,甲队接种2250人与乙队接种1800人用时相同,问甲队每小时接种多少人?23. 阅读感悟:
(1)、本次共调查了人;(2)、补全条形统计图,扇形统计图中“跑步”所对应的扇形的圆心角的度数是 ▲ ;(3)、估计小区居民2000人中喜欢打太极的有多少人.21. 先化简,再求值: ,其中, , .22. 根据疫情防控工作需要,某社区组织甲、乙两支医疗队开展疫苗接种工作,甲队比乙队每小时多接种30人,甲队接种2250人与乙队接种1800人用时相同,问甲队每小时接种多少人?23. 阅读感悟:有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:
已知实数x、y满足 ①, ②,求 和 的值.
本题常规思路是将①②两式联立组成方程组,解得x、y的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由 可得 ,由 可得 .这样的解题思想就是通常所说的“整体思想”.
解决问题:
(1)、已知二元一次方程组 ,则 ;(2)、某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需元.(3)、对于实数x、y,定义新运算: ,其中a、b、c是常数,等式右边是通常的加法和乘法运算,已知 , ,那么 .24. 如图①, , 被直线 所截,点D是线段 上的点,过点D作 ,连结 , . (1)、请说明(2)、将线段 沿着直线 平移得到线段 ,连结 .
(1)、请说明(2)、将线段 沿着直线 平移得到线段 ,连结 .a.如图②,当 时,则 的度数为 ;
b.在整个运动中,当 时, .