陕西省西安市莲湖区2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-08-11 类型：期末考试

进入出卷网下载

一、选择题（本大题共8个小题，每小题3分，共24分.）

1. 函数 $y = \frac{2022}{x}$ 的图象是（）

A、直线 B、线段 C、双曲线 D、抛物线

查看试题解析
2. 一元二次方程 $x^{2} = x$ 的解为（）

A、 $- x = 1$ B、 $x_{1} = x_{2} = 1$ C、 $x_{1} = 0 ， x_{2} = 1$ D、 $x_{1} = x_{2} = 0$

查看试题解析
3. 如图所示，下列几何体中三视图都是圆的是（）

A、 B、 C、 D、

查看试题解析
4. 一直角三角形的两条直角边长分别为6和8，它斜边上的中线长为（）

A、5 B、4 C、3 D、2

查看试题解析
5. 如图1是某淘宝店新推出的鞋架，可抽象成图2，直线 $l_{1} ∥ l_{2} ∥ l_{3}$ ，直线 $A C$ 和 $D F$ 被 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 所截，如果 $A B = 30 cm$ ， $B C = 50 cm$ ， $E F = 40 cm$ ，那么 $D E$ 的长是（）

A、 $\frac{320}{3} cm$ B、 $\frac{200}{3} cm$ C、64cm D、24cm

查看试题解析
6. 陕西是中华文明和中华民的发源地之一，周秦汉唐故里，旅游资源非常丰富，在今年“十一”期间，小康和小明两家准备从华山、华阳古镇，太白山三个著名景点中各选择一个景点旅游，他们通过抽签的方式确定景点，那么他们两家恰好能抽到同一景点的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{1}{3}$

查看试题解析
7. 如图所示，反比例函数 $y_{1} = \frac{k_{1}}{x} (x < 0)$ 的图像经过点A（－2，a），B（－a＋2，6），它与正比例函数 $y_{2} = k_{2} x$ 的图像交于点A，则下列结论正确的是（）

A、 $k_{1} = - \frac{3}{2}$ B、 $a = 3$ C、 $k_{2} = - 6$ D、反比例函数 $y_{1}$ 与正比例函数 $y_{2}$ ，都随x的增大而减小

查看试题解析
8. 如图，∠ABD=∠CBE=90°， AB=BD， ∠CAB=∠E．若BE=10， AD= $4 \sqrt{2}$ ，则 $\frac{A C}{D E}$ 的值为（）

A、 $\frac{7}{10}$ B、 $\frac{3}{5}$ C、 $\frac{1}{2}$ D、 $\frac{2}{5}$

查看试题解析

二、填空题（本大题共5个小题，每小题3分，共15分）

9. 若 $(m - 3) x^{2} - x + 1 = 0$ 是关于x的一元二次方程，则m的取值范围是．

查看试题解析
10. 如图是康康的健康绿码示意图，用黑白打印机打印于边长为10cm的正方形区域内，为了估计图中黑色部分的总面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.65左右，据此可以估计黑色部分的总面积约为cm² ．

查看试题解析
11. 若 $△ A B C \sim △ D E F$ ，且 $\frac{S_{△ A B C}}{S_{△ D E F}} = \frac{9}{16}$ ，则 $\frac{A B}{D E} =$ ．

查看试题解析
12. 如图所示，点B，A分别在反比例函数 $y_{1} = \frac{a}{x}$ 和 $y_{2} = \frac{b}{x}$ 的图象上，AB//x轴，点C在x轴的负半轴上，若 $S_{△ A B C} = 6$ 则a－b的值为．

查看试题解析
13. 如图所示，在矩形ABCD中，对角线AC与BD相交于点O，延长AB到E，使 $B E = A B$ ，连接CE，点F是AE上任意一点，过点F作FH⊥AC于点H，FG⊥CE于点G，若 $∠ D A C = 30 °$ ，BD＝2，则FH＋FG的值为．

查看试题解析

三、解答题（本大题共13个小题，共81分.）

14. 已知 $\frac{x}{y} = \frac{3}{5}$ ，求 $\frac{x - y}{x + y}$ 的值．

查看试题解析
15. 解方程 $x^{2} - 9 = 7 (x + 3)$ ．

查看试题解析
16. 已知反比例函数 $y = \frac{2 k - 3}{x}$ 的图象位于第二、四象限，正比例函数 $y = k x$ 图象经过第一、三象限，求k的整数值．

查看试题解析
17. 以C为位似中心，将△ABC放大，使得放大后的△CDE与△ABC的相似比为2∶1（点D，E分别是点A，B的对应点），要求所画△CDE与△ABC在点C的两侧．

查看试题解析
18. 如图所示，在四边形ABCD中， $A D ∥ B C$ ，点E是对角线BD上一点， $∠ A E B = ∠ A D C$ ，求证 $△ A D E ∽ △ D B C$ ．

查看试题解析
19. 如图所示，矩形AOBC的边AO，OB在两坐标轴上，双曲线 $y = \frac{8}{x}$ 与矩形AOBC的边交于点D，E，点C（8，5），求D，E两点的坐标．

查看试题解析
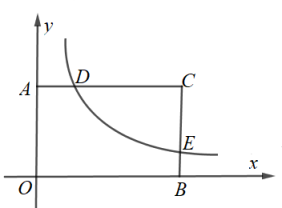20. 如图所示，某校园有杆AB，它在阳光下某一时刻的影子长为AG，高1.6米的标杆EF在阳光下同一时刻的影子为EM，AB，EF都与地面垂直，小媛通过测量获得数据 $A G = 2.5$ 米， $E M = 1$ 米，求旗杆AB的高度．

查看试题解析
21. 陕西重型汽车有限公司（简称陕汽重卡）是由湘火炬汽车集团股份有限公司与陕西汽车集团有限责任公司合资组建大型汽车公司企业，该企业随着生产技术的不断提升，生产的某款汽车的价格由2021年8月份的39万元/辆下降到10月份的31.59万元/辆，若月平均降价的百分率保持不变，试求月平均降价率．

查看试题解析
22. 如图①所示是一个正三棱锥（即正四面体）骰子的实物示意图，图②是它的立体示意图，它有四个面，各面分别标有数字5，4，4，7．

(1)、小康将这枚正三棱锥骰子随机抛掷一次，则掷得的数字是偶数的概率为．

(2)、小齐随机抛掷两次骰子，试用列表法或画树状图法求两次掷得的数字和不小于11的概率．

查看试题解析
23. 已知关于x的一元二次方程 $(k - 2) x^{2} - 2 x + 1 = 0$ ．

(1)、若方程有两个不相等的实数根，求k的取值范围．

(2)、从－4，－2，0，2，4中任选一个数字作为k代入原方程，求选取的数字能令方程有实数根的概率．

查看试题解析
24. 如图，在菱形ABCD中，两条对角线相交于点O，F是边CD的中点，连接OF并延长到E，使FE=OF，连接CE，DE．

(1)、求证：四边形OCED是矩形：

(2)、若∠DAB=60°，菱形ABCD 面积为 $8 \sqrt{3}$ ，求矩形OCED的周长．

查看试题解析
25. 西安市某校为进一步预防“新型冠状病毒”，对全校所有的教室都进行了“熏药法消毒”处理，已知该药物在燃烧释放过程中，教室内空气中每立方米的含药量y（mg）与燃烧时间x（min）之间的函数关系如图所示，其中当x＜6时，y是x的正比例函数，当 $x \geq 6$ 时，y是x的反比例函数，根据图象提供的信息，解答下列问题：

(1)、求当x≥6时，y与x的函数关系式．

(2)、求点A的坐标．

(3)、药物燃烧释放过程中，若空气中每立方米的含药量不小于1.5mg的时间超过30分钟，即为有效消毒，请问本题中的消毒是否为有效消毒？

查看试题解析
26. 问题提出：

(1)、如图1，在四边形ABCD中 $∠ A B C = 90^{\circ}$ ，对角线AC⊥BD，AC＝BD，E，F，G，H分别是各边的中点，求证：四边形EFGH是正方形．
问题解决：

(2)、如图2，某市有一块四边形土地ABCD，AD＝60米，DC＝80米，∠ADC是直角，P是该四边形土地内的一点，计划在四个三角形土地△APD，△APB，△BCP，△CPD中分别种植不同的花草，为了方便种植，王师傅设计出如下方案：取四边形ABCD各边的中点E，F，G，H，然后在四边形EFGH的四条边EF，FG，GH，EH铺上人行道地砖（人行道宽度不计），铺设地砖成本为20元/米，经测量AP＝BP，CP＝DP，∠APB＝∠CPD＝90°，设计要求是四边形EFGH为正方形，请问王师傅的设计方案是否符合要求，若符合，请写出证明过程，并计算铺设地砖所需的费用；若不符合，请说明理由．

查看试题解析