四川省广元市剑阁县2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-11 类型：期末考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分．

1. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{3}$ B、 $\sqrt{\frac{1}{5}}$ C、 $\sqrt{0.8}$ D、 $\sqrt{9}$

查看试题解析
2. 下列四组线段中，能作为直角三角形三条边的是（）

A、1、2、3 B、2、3、4 C、3、4、5 D、5、12、14

查看试题解析
3. 下列各图中，不能表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
4. 某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：

尺码

$39$

$40$

$41$

$42$

$43$

平均每天销售数量（件）

$10$

$12$

$20$

$12$

$12$

该店主决定本周进货时，增加了一些 $41$ 码的衬衫，影响该店主决策的统计量是（）

A、平均数 B、方差 C、众数 D、中位数

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{{(- 5)}^{2}} = - 5$ B、 $3 \sqrt{5} - \sqrt{5} = 3$ C、 $\sqrt{4 + 9} = \sqrt{4} + \sqrt{9}$ D、 ${(- 3 \sqrt{2})}^{2} = 18$

查看试题解析
6. 关于函数 $y = - 2 x + 1$ ，下列结论正确的是（）

A、图象必经过点 $(- 2, 1)$ B、图象经过第一、二、三象限 C、当 $x > \frac{1}{2}$ 时， $y < 0$ D、y随x的增大而增大

查看试题解析
7. 如图，A，B两点分别位于一个池塘的两端，小聪想用绳子测量A，B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A，B的点C，找到AC，BC的中点D，E，并且测出DE的长为10m，则A，B间的距离为（）

A、15m B、25m C、30m D、20m

查看试题解析
8. 矩形、菱形、正方形都具有的性质是（　　）

A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分对角

查看试题解析
9. 如图函数y=2x和y=ax+4的图象相交于A(m，3)，则不等式2x<ax+4的解集为（）

A、 $x < \frac{3}{2}$ B、 $x < 3$ C、 $x > \frac{3}{2}$ D、 $x > 3$

查看试题解析
10. 已知 $A$ ， $B$ 两地间有汽车站 $C$ ，客车由 $A$ 地驶向 $C$ 站、货车由 $B$ 地经过 $C$ 站去 $A$ 地（客货车在 $A$ ， $C$ 两地间沿同一条路行驶），两车同时出发，匀速行驶，（中间不停留）货车的速度是客车速度的 $\frac{3}{4}$ ．如图所示是客、货车离 $C$ 站的路程与行驶时间之间的函数关系图象．小明由图象信息得出如下结论：①客车速度为60千米/时；②货车由 $B$ 地到 $A$ 地用14小时；③货车由 $B$ 地出发行驶120千米到达 $C$ 站；④客车行驶480千米时与货车相遇．你认为正确的结论有（）个

A、0 B、1 C、2 D、3

查看试题解析

二、填空题：本题共6小题，每小题4分，共24分．

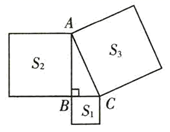
11. 若二次根式 $\sqrt{3 - x}$ 有意义，则x的取值范围为．

查看试题解析
12. 若菱形的两条对角线长分别是6cm，8cm，则该菱形的面积是cm² ．

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ，分别以 $B C$ 、 $A B$ 、 $A C$ 为边向外作正方形，面积分别记为 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ ，若 $S_{2} = 4$ ， $S_{3} = 6$ ，则 $S_{1} =$ ．

查看试题解析
14. 若一组数据4，x ， 5，7，9的平均数为6，则这组数据的方差为．

查看试题解析
15. 如图所示，圆柱形玻璃容器，高19cm，底面周长为30cm，在外侧下底面点 $S$ 处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口内侧距开口处1cm的点 $F$ 处有一飞蛾，急于捕获飞蛾充饥的蜘蛛，所走的最短路线的长度是cm．（玻璃容器壁厚度忽略不计）

查看试题解析
16. 如图，点P是正方形 $A B C D$ 的对角线 $B D$ 上一点， $P E ⊥ B C ， P F ⊥ C D$ ，垂足分别为点E ， F ，连接 $A P ， E F$ ，给出下列四个结论：① $A P = E F$ ；② $∠ P F E = ∠ B A P$ ；③ $P D = \sqrt{2} E C$ ；④ $△ A P D$ 一定是等腰三角形．其中正确的结论序号是．

查看试题解析

三、解答题：共96分．

17. 计算： $| \sqrt{3} - 2 | + {(π - \sqrt{10})}^{0} - \sqrt{12} + {(- \frac{1}{2})}^{- 2}$

查看试题解析
18. 如图，在平行四边形 $A B C D$ 中， $M ， N$ 分别是边 $A B ， C D$ 的中点；求证： $A N$ ∥ $M C$

查看试题解析
19. 已知 $y = \sqrt{x - 2} + \sqrt{2 - x} + \frac{3}{8}$ ，求 $\sqrt{x y}$ 的值．

查看试题解析
20. 为了倡导“节约用水，从我做起”，黄岗市政府决定对市直机关500户家庭的用水情况作一次调查，市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量（单位：吨），并将调查结果制成了如图所示的条形统计图.

(1)、请将条形统计图补充完整；

(2)、求这100个样本数据的平均数，众数和中位数；

(3)、根据样本数据，估计黄岗市直机关500户家庭中月平均用水量不超过12吨的约有多少户？

查看试题解析
21. 如图，四边形 $A B C D$ 是我县某校在校园一角开辟的一块四边形的“试验田”，经过测量得知 $∠ B = 90 ° ， A B = 24 m ， B C = 7 m ， C D = 15 m ， A D = 20 m$ ．求四边形 $A B C D$ 的面积．

查看试题解析
22. 在矩形ABCD中，点E在BC上，AE=AD，DF⊥AE，垂足为F．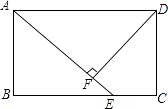

(1)、求证．DF=AB；

(2)、若∠FDC=30°，且AB=4，求AD．

查看试题解析
23. 习近平总书记说：“人民群众多读书，我们的民族精神就会厚重起来、深邃起来．”某书店计划在4月23日世界读书日之前，同时购进A，B两类图书，已知A类图书每本的进价36元，B类图书每本的进价45元．

(1)、该书店计划用4500元全部购进两类图书，设购进A类x本，B类y本．求y关于x的关系式；

(2)、进货时，A类图书的购进数量不少于60本，已知A类图书每本的售价为38元，B类图书每本的售价为50元，若书店全部售完可获利W元，求W关于x的关系式，并说明应该如何进货才能使书店所获利润最大，最大利润为多少元？

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，直线 $A B$ 与 $x$ 轴、 $y$ 轴分别交于点 $A$ 、点 $B$ ，直线 $C D$ 与 $x$ 轴、 $y$ 轴分别交于分别交于点 $C$ 、点 $D$ ，直线 $A B$ 的解析式为 $y = - \frac{5}{8} x + 5$ ，直线 $C D$ 的解析式为 $y = k x + b (k \neq 0)$ ，两直线交于点 $E (m ， \frac{10}{3})$ ，且 $O B ： O C = 5 ： 4$ .

(1)、求直线 $C D$ 的解析式；

(2)、将直线 $C D$ 向下平移一定的距离，使得平移后的直线经过 $A$ 点，且与 $y$ 轴交于点 $F$ ，求四边形 $A E D F$ 的面积.

查看试题解析
25. 如图

(1)、数学课上，张老师给出了一个问题：如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角∠DCG的平分线CF于点F．求证：AE＝EF．小明经过思考展示了一种正确的解题思路：取AB的中点H，连接HE，则可以证明AE＝EF．
请你写出证明过程．

(2)、在此基础上，小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B、C外）的任意一点”，其他条件不变，那么结论“AE＝EF”仍然成立，你认为小颖的观点正确吗？如果正确，请写出证明过程；如果不正确，请说明理由；

(3)、如图3，如果点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE＝EF”仍然成立吗？直接写出结论，不用说明理由．

查看试题解析
26. 如图，已知直线 $y = k x + b$ 经过 $A (6 ， 0)$ ， $B (0 ， 3)$ 两点．

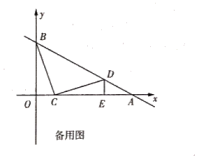(1)、求直线 $y = k x + b$ 的解析式；

(2)、若C是线段OA上一点，将线段CB绕点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上.
①求点C和点D的坐标；

②若点P在y轴上，Q在直线AB上，是否存在以C，D，P，Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点Q的坐标，否则说明理由．

查看试题解析

尺码	$39$	$40$	$41$	$42$	$43$
平均每天销售数量（件）	$10$	$12$	$20$	$12$	$12$