陕西省渭南市临渭区2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-08-11 类型:期末考试
一、选择题(共8小题,每小题3分,计24分.)
-
1. 若 ,则下列各不等式不一定成立的是( )A、 B、 C、 D、2. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
3. 下列命题正确的是( )A、三角形三条角平分线的交点到三角形三个顶点的距离都相等 B、两条对角线相等的四边形是平行四边形 C、分式 的值不能为零 D、用反证法证明“三角形中必有一个角不大于60”,先假设这个三角形中有一个内角大于60°4. 下列等式成立的是( )A、 B、 C、 D、5. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )
斐波那契螺旋线
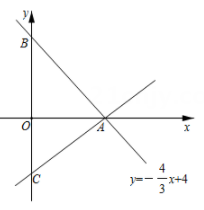
3. 下列命题正确的是( )A、三角形三条角平分线的交点到三角形三个顶点的距离都相等 B、两条对角线相等的四边形是平行四边形 C、分式 的值不能为零 D、用反证法证明“三角形中必有一个角不大于60”,先假设这个三角形中有一个内角大于60°4. 下列等式成立的是( )A、 B、 C、 D、5. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )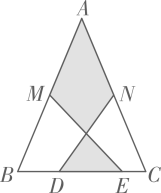 A、25cm2 B、35cm2 C、30cm2 D、42cm26. 九年级(3)班小王和小张两人练习跳绳,小王每分钟比小张少跳60个,小王跳120个所用的时间和小张跳180个所用的时间相等.设小王跳绳速度为x个每分钟,则列方程正确的是( )A、 B、 C、 D、7. 如图, 为 轴负半轴上一点,过点 作 轴,与直线 交于点 ,将 沿直线 向上平移 个单位长度得到 ,若点 的坐标为 ,则点 的坐标是( )
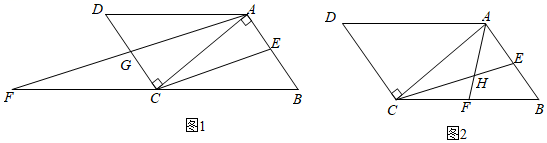
A、25cm2 B、35cm2 C、30cm2 D、42cm26. 九年级(3)班小王和小张两人练习跳绳,小王每分钟比小张少跳60个,小王跳120个所用的时间和小张跳180个所用的时间相等.设小王跳绳速度为x个每分钟,则列方程正确的是( )A、 B、 C、 D、7. 如图, 为 轴负半轴上一点,过点 作 轴,与直线 交于点 ,将 沿直线 向上平移 个单位长度得到 ,若点 的坐标为 ,则点 的坐标是( )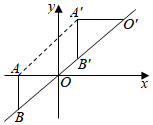 A、 B、 C、 D、8. 如图,四边形 是平行四边形,点 是边 上一点,且 , 交 于点 , 是 延长线上一点,连接 、 ,下列结论:① 平分 ;② 平分 ;③ ;④ .其中正确结论的个数为( )
A、 B、 C、 D、8. 如图,四边形 是平行四边形,点 是边 上一点,且 , 交 于点 , 是 延长线上一点,连接 、 ,下列结论:① 平分 ;② 平分 ;③ ;④ .其中正确结论的个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(共5小题,每小题3分,计15分)
-
9. 当x的值是时,分式的值为零.10. 如图,正八边形和正五边形按如图方式拼接在一起,则 .
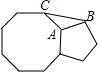 11. 已知一次函数 和 ,假设 且 ,如果关于 、 的二元一次方程组 的解为 ,那么 0.12. 如图,在 中, ,点 为线段 上一点,连接 将 沿 翻折,点 的对应点 落在 的延长线上,若 则 .
11. 已知一次函数 和 ,假设 且 ,如果关于 、 的二元一次方程组 的解为 ,那么 0.12. 如图,在 中, ,点 为线段 上一点,连接 将 沿 翻折,点 的对应点 落在 的延长线上,若 则 .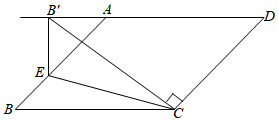 13. 如图,已知△ABC(AB > AC)中,∠BAC = 60°,AC = 4,D为BC边上的中点,过点D的直线DF将△ABC的周长平分且交AB于点F,则DF的长为 .
13. 如图,已知△ABC(AB > AC)中,∠BAC = 60°,AC = 4,D为BC边上的中点,过点D的直线DF将△ABC的周长平分且交AB于点F,则DF的长为 .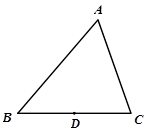
三、解答题(共12小题,计81分.)
-
14. 计算:15. 解不等式组并把解集表示在数轴上:16. 分解因式:(1)、 ;(2)、 .17. 先化简,再求值: ,其中 .18. 解方程:19. 如图所示,在 中,请用尺规作图法在 边上做一点 ,使得 的周长等于边 的长与边 的长之和.(不写作法,保留作图痕迹)
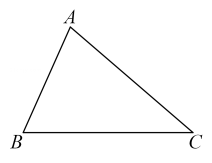 20. 如图,和都是等腰三角形,且 , , B,C,D在同一条直线上.求证:≌.
20. 如图,和都是等腰三角形,且 , , B,C,D在同一条直线上.求证:≌.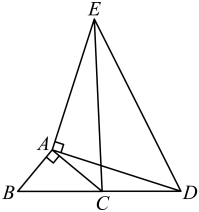 21. 端午节前夕,某商铺用1200元购进批发价分别为每袋30元和50元的蜜枣粽、肉粽进行销售,并分别以每袋35元与60元的价格售出,设购进蜜枣粽x袋,肉粽y袋.(1)、若该商铺将粽子全部售出共赚了215元,则购进蜜枣粽和肉粽各多少袋?(2)、若要求购进密枣粽的数量不得少于肉粽的数量,则应该如何分配购进的两种粽子的数量并全部售出才能获得最大利润?此时最大利润是多少?22. 数学探究课上老师出了这样一道题:“如图,等边 中有一点 ,且 , , ,试求 的度数.”小明和小军探讨时发现了一种求 度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断.
21. 端午节前夕,某商铺用1200元购进批发价分别为每袋30元和50元的蜜枣粽、肉粽进行销售,并分别以每袋35元与60元的价格售出,设购进蜜枣粽x袋,肉粽y袋.(1)、若该商铺将粽子全部售出共赚了215元,则购进蜜枣粽和肉粽各多少袋?(2)、若要求购进密枣粽的数量不得少于肉粽的数量,则应该如何分配购进的两种粽子的数量并全部售出才能获得最大利润?此时最大利润是多少?22. 数学探究课上老师出了这样一道题:“如图,等边 中有一点 ,且 , , ,试求 的度数.”小明和小军探讨时发现了一种求 度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断.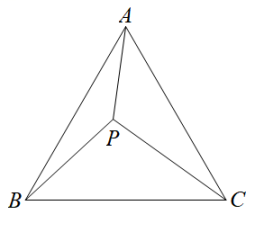 (1)、在图中画出 绕点 顺时旋转60°后的 ,并判断 的形状是 ;(2)、试判断 的形状,并说明理由;(3)、由(1)、(2)两问可知: .23. 劳动教育是国民教育体系的重要内容,具有树德、增智、强体、育美等综合育人价值,某校密切联合家庭开展劳动教育课程.暑假期间,部分家长组织学生到户外开展劳动实践活动,一名学生带一名家长,家长联系了甲乙两家组织机构,他们的报价相同,每位学生的报价比家长少20元,按报价计算,家长的总费用为50000元,学生的总费用为48000元.(1)、求家长和学生报价分别是多少元?(2)、经协商,甲机构的优惠条件是:家长全价,学生都按七折收费﹔乙机构的优惠条件是家长、学生都按 为整数)折收费,他们选择了总费用较少的乙机构,请问 的最大值为多少?
(1)、在图中画出 绕点 顺时旋转60°后的 ,并判断 的形状是 ;(2)、试判断 的形状,并说明理由;(3)、由(1)、(2)两问可知: .23. 劳动教育是国民教育体系的重要内容,具有树德、增智、强体、育美等综合育人价值,某校密切联合家庭开展劳动教育课程.暑假期间,部分家长组织学生到户外开展劳动实践活动,一名学生带一名家长,家长联系了甲乙两家组织机构,他们的报价相同,每位学生的报价比家长少20元,按报价计算,家长的总费用为50000元,学生的总费用为48000元.(1)、求家长和学生报价分别是多少元?(2)、经协商,甲机构的优惠条件是:家长全价,学生都按七折收费﹔乙机构的优惠条件是家长、学生都按 为整数)折收费,他们选择了总费用较少的乙机构,请问 的最大值为多少?