四川省南充市2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-11 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $\sqrt{2} - \sqrt{\frac{1}{2}}$ ，结果是（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{2}}{4}$ C、 $\frac{3 \sqrt{2}}{4}$ D、 $\frac{\sqrt{2}}{3}$

查看试题解析
2. 函数 $y = \sqrt{2 x - 4}$ 中，自变量 $x$ 的取值范围是（）

A、 $x \neq 2$ B、 $x > 0$ C、 $x \geq 2$ D、 $x > 2$

查看试题解析
3. 下列各组数据，是勾股数的为（）

A、1，1， $\sqrt{2}$ B、0.6，0.8，1 C、4，5，6 D、8，15，17

查看试题解析
4. 在 $▱ A B C D$ 中， $∠ A + ∠ B + ∠ C = 240 °$ ，则 $∠ A$ 的度数是（）

A、 $80 °$ B、 $70 °$ C、 $60 °$ D、不能确定

查看试题解析
5. 数学李老师回忆当年大学毕业参加公招，笔试成绩88分，进入前二分之一再面试．这个描述用到的统计量是所有笔试者成绩的（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
6. 若点 $A (1 ， m)$ 与点 $B (3 ， n)$ 都在直线 $y = - \sqrt{2} x + 1$ 上，则 $m$ 与 $n$ 的关系是（）

A、 $m > n$ B、 $m < n$ C、 $m = n$ D、不能确定

查看试题解析
7. 下表记录了数学兴趣小组甲、乙、丙、丁四名同学最近几次拓展训练数学成绩的平均分与方差．要推选一名成绩好且发挥稳定的同学参加学校比赛，应推选（）

甲

乙

丙

丁

平均分

92

95

95

92

方差

3.6

3.6

7.4

8.1

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 如图， $△ A B C$ 中， $∠ B = 45 °$ ， $B C = 2 \sqrt{2}$ ， $D$ 是边 $A B$ 靠近点 $B$ 的三等分点， $∠ A D C = ∠ A$ ，则 $C D$ 长为（）

A、2 B、 $\frac{5}{2}$ C、 $\sqrt{5}$ D、 $\sqrt{6}$

查看试题解析
9. 如图，已知 $A (1 ， 3)$ ， $B (5 ， 1)$ ，若直线 $y = k x + 1$ 与线段 $A B$ 有公共点，则 $k$ 的取值范围是（）

A、 $k \neq 0$ B、 $k > 1$ C、 $0 \leq k \leq 1$ D、 $0 \leq k \leq 2$

查看试题解析
10. 如图，矩形 $A B C D$ 中， $M$ ， $N$ 分别是边 $A B$ ， $C D$ 的中点， $B P ⊥ A N$ 于 $P$ ， $C P$ 的延长线交 $A D$ 于 $Q$ ．下列结论：① $P M = C N$ ；② $P M ⊥ C Q$ ；③ $P Q = A Q$ ；④ $D Q < 2 P N$ ．其中结论正确的有（）

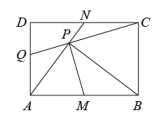A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 要使 $n$ 和 $\sqrt{45 n}$ 都是正整数，则 $n$ 最小为．

查看试题解析
12. 已知等腰ΔABC中，AB＝AC＝5，BC＝6，则ΔABC的面积为.

查看试题解析
13. “六·一”儿童节，学校六（1）班王老师带领班上 $x$ 名学生参观植物博览园．成人票单价20元，学生票单价10元．总费用 $y$ （元）与 $x$ 的函数关系式为．（不要求写自变量取值范围）

查看试题解析
14. 从－1，0， $\frac{1}{2}$ ，2中任取两个不同的数求积，不同算式构成的积的众数是．

查看试题解析
15. 如图，在 $▱ A B C D$ 中， $M$ 在边 $A D$ 上， $E$ ， $F$ 分别是 $B M$ ， $C M$ 的中点，若 $A M = 2 D M$ ，则 $\frac{E F}{D M} =$ ．

查看试题解析
16. 如图，直线 $y = - \frac{1}{2} x + 2$ 与 $x$ 轴交于 $A$ ，与 $y$ 轴交于 $B$ ，点 $P$ 在经过点 $B$ 的直线 $y = \frac{1}{3} x + b$ 上，当 $△ P A B$ 是等腰直角三角形时，点 $P$ 的坐标是．

查看试题解析

三、解答题

17. 计算： $\sqrt{3} \times \sqrt{15} + \sqrt{1 \frac{4}{5}} - \frac{20 \sqrt{2}}{\sqrt{10}}$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = 2 \sqrt{3}$ ， $A C = \sqrt{6}$ ， $D$ 是 $B C$ 上一点， $A D = \sqrt{10}$ ， $C D = 2$ ．求 $∠ B$ 的度数．

查看试题解析
19. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $D$ ， $E$ 分别是边 $B C$ ， $A C$ 的中点， $F$ 在 $D E$ 的延长线上， $A F = B D$ ．求证： $C F = C D$ ．

查看试题解析

20. 学校举行“英语单词听写比赛”，八（1）班男生、女生各选出10人参加学校决赛．成绩如下：

男生：100，95，95，90，90，90，85，85，80，80；

女生：100，95，95，90，90，90，90，85，85，80．

(1)、完善分析数据表，并写出女生成绩方差的计算过程．

	平均分	中位数	众数	方差
男生	89		90	39
女生		90

(2)、由分析数据，评估这个班男生、女生选手成绩．

查看试题解析

21. 如图，一次函数 $y = k x + b (k \neq 0)$ 的图象与正比例函数 $y = - \frac{4}{3} x$ 的图象交于点 $A (m ， 4)$ ，与 $x$ 轴交于点 $B$ ，与 $y$ 轴交于点 $C$ ， $O C = \frac{5}{2}$ ．

(1)、求一次函数的解析式．

(2)、比较 $∠ O A C$ 与 $∠ O B C$ 的大小，并说明理由．

查看试题解析
22. 如图，将矩形纸片 $A B C D$ 沿 $E F$ 折叠，使顶点 $C$ 与顶点 $A$ 重合，点 $D$ 落在点 $G$ 处．

(1)、点 $C$ ， $F$ ， $G$ 三点是否共线？并说明理由．

(2)、若 $A B = 4$ ， $B C = 8$ ，求折叠后纸片重合部分的面积．

查看试题解析

23. 某商店今年春季分两次订购

A

，

B

两种商品销售，同种商品前后进价相同，具体情况如下表．

批次	$A$ 件数（件）	$B$ 件数（件）	总价（元）
第一次	30	40	3800
第二次	40	30	3200

(1)、求这两种商品订货的单价．

(2)、夏季来临，需求增加，商店计划再订购这两种商品共1000件，其中

A

种件数不少于

B

种件数的4倍．销售价每件

A

种30元，

B

种100元．求夏季销售这两种商品的毛利

W

（元）与再订购

A

种商品件数

m

之间的函数关系式．并求最大毛利．

查看试题解析

24. 如图， $▱ A B C D$ 中， $A C ⊥ B C$ ， $A E ⊥ C D$ 与射线 $B C$ 交于 $E$ ， $C E = A C$ ．

(1)、判断四边形 $A C E D$ 的形状，并证明．

(2)、 $P$ 是 $C D$ 上的动点， $P M ∥ A E$ ， $P N ⊥ A P$ ， $M$ ， $N$ 在射线 $B C$ 上．求证：线段 $M N$ 为定长（长度不变）．

查看试题解析
25. 如图，矩形 $O A B C$ 在直角坐标系中，顶点 $B$ 的坐标为 $(4 ， n)$ ，对角线 $O B$ ， $A C$ 交于 $D$ ．直线 $y = \frac{3}{4} n x - \frac{3}{2} n$ 分别与 $O A$ ， $A C$ ， $O B$ 交于 $P$ ， $M$ ， $N$ ．

(1)、求 $D P$ 的长．（用含 $n$ 的式子表示．）

(2)、 $M$ 是否为线段 $P N$ 的中点？请说明理由．

(3)、当 $C N = 2 M N$ 时，求 $n$ 的值．

查看试题解析

	甲	乙	丙	丁
平均分	92	95	95	92
方差	3.6	3.6	7.4	8.1