四川省自贡市2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-11 类型：期末考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{x - 3}$ 有意义,则实数x取值范围是（）

A、 $x \leq 3$ B、 $x < 3$ C、 $x > 3$ D、 $x \geq 3$

查看试题解析
2. 如图，已知 $A (1 ， 2)$ ，连接 $O A$ ，以原点 $O$ 为圆心， $O A$ 长为半径画弧，交 $x$ 轴正半轴于点 $B$ ，则点 $B$ 坐标为（）

A、（0，2） B、（0， $\sqrt{5}$ ） C、（2，0） D、（ $\sqrt{5}$ ， 0）

查看试题解析
3. 甲、乙、丙、丁四位同学五次数学测验成绩统计如下表，如果从这四位同学中，选出一位平均成绩较高且状态稳定的同学参加数学比赛，那么应选（）
人员
甲
乙
丙
丁
平均数
81
86
86
82
方差
40
45
55
59

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 下列变形正确的是（）

A、 $\sqrt{7} - \sqrt{5} = \sqrt{2}$ B、 $5 \times \sqrt{\frac{3}{5}} = \sqrt{3}$ C、 $\sqrt{{(- 2)}^{2}} = - 2$ D、 $\sqrt{12} \div 2 = \sqrt{3}$

查看试题解析
5. 一次函数 $y = - 2 x + 3$ 图象经过点 $(- 3 ， y_{1}) ， (- 2 ， y_{2})$ ，则以下判断正确的是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、无法确定

查看试题解析
6. 如图，平行四边形 $A B C D$ 的对角线 $A C ， B D$ 相交于于点 $O$ ， $O E / / A B$ 交 $A D$ 于点 $E$ ；若 $A C = 2$ ， △ $A O E$ 的周长等于4，则平行四边形 $A B C D$ 的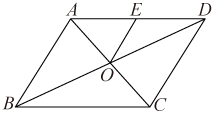周长等于（）

A、16 B、14 C、12 D、10

查看试题解析
7. 一次函数 $y_{1} = m x + n$ 和 $y_{2} = k x + b$ 的图象如图所示，下列结论：

① $k < 0$ ；② $n > 0$ ；③方程 $(k - m) x = n - b$ 的解是 $x = - 1$ ；④不等式 $m x + n > k x + b$ 的解集 $x < - 1$

其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，在 $R t$ △ $A B C$ 中， $∠ A C B = 9 0^{∘} ， A C = 3 ， B C = 4$ ，斜边 $A B$ 的垂直平分线 $D E$ 交 $A B$ 于点 $D$ ，交 $A C$ 的延长线于点 $E$ ，连接 $B E$ ；则 $D E$ 的长为（）

A、 $\frac{11}{3}$ B、 $\frac{10}{3}$ C、 $\frac{17}{5}$ D、 $\frac{16}{5}$

查看试题解析

二、填空题

9. 在平行四边形 $A B C D$ 中， $∠ A = 4 0^{∘}$ ，则 $∠ B$ 的度数是．

查看试题解析
10. 在二次根式 $\sqrt{15}$ ， $\sqrt{20}$ ， $\sqrt{\frac{2}{3}}$ ， $\sqrt{0.4}$ 中，最简二次根式有个．

查看试题解析
11. 将一次函数 $y = - 5 x + 3$ 的图象沿 $y$ 轴向下平移个单位长度后，可以得到正比例函数 $y = - 5 x$ 的图象．

查看试题解析
12. 某地10家电商6月份的销售额如下表所示，销售额的中位数为万元．
销售额（万元）
1
2
3
11
电商（家）
1
4
3
2

查看试题解析
13. 在 $R t$ △ $A B C$ 中， $∠ C = 9 0^{∘}$ ；若 $c + b = 18$ ， $c - b = 2$ ，则 $a$ = ．

查看试题解析
14. 如图①，点 $E$ 为□ $A B C D$ 边上的一个动点，并沿 $A \to B \to C \to D$ 的路径移动到点 $D$ 停止；设点 $E$ 经过的路径长为 $x$ ， △ $A D E$ 的面积为 $y$ ， $y$ 与 $x$ 的函数图象如图②所示；若 $∠ C = 6 0^{∘}$ ，则□ $A B C D$ 的面积是．

查看试题解析

三、解答题

15. 已知 $x = \sqrt{5} - 1$ ，求代数式 $x^{2} + 2 x - 3$ 的值．

查看试题解析
16. 如图，在□ $A B C D$ 中， $A F$ ∥ $C E$ ；求证： $B E = D F$ ．

查看试题解析
17. 如图，在4×4的正方形网格中，每个小方格的顶点叫做格点，以格点为顶点分别按下列要求画图出图形．

(1)、在图①中，画一个斜边长为 $3 \sqrt{2}$ 的等腰直角三角形；

(2)、在图②中，画一个面积为10的正方形．

查看试题解析
18. 如图，四边形 $A B C D$ 是矩形，点 $E$ 在 $A D$ 上， $E F ⊥ E C$ 交 $A B$ 于点 $F$ ，且 $E F = E C$ ， $D E = 2$ ，矩形的周长为16；求 $A E$ 的长．

查看试题解析
19. 如图，一次函数 $y = x + 6$ 的图象与 $x$ 轴， $y$ 轴分别交于 $A ， B$ 两点，与正比例函数 $y = - 2 x$ 的图象交于点 $P$ ．

(1)、求点 $P$ 的坐标；

(2)、求 $A P ： P B$ 的值．

查看试题解析
20. 某校开展了一次党史知识竞赛（竞赛成绩为百分制），并随机抽取了50名学生的竞赛成绩，经过整理数据，得到以下信息：
信息一：50名学生竞赛成绩的频数分布直方图如图所示（数据分成5组： $50 \leq x < 60$ ， $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x \leq 100$ ．），从左到右依次为第一组到第五组．
信息二：第三组的成绩（单位：分）分别为：71， 72， 73， 74， 74， 74， 75， 75， 76， 76， 77， 79．
根据信息解答下列问题：

(1)、补全频数分布直方图（直接在图中补全）；

(2)、第三组竞赛成绩的众数是分，估算所抽取的50名学生竞赛成绩的平均分约为分．

(3)、若该校共有1500名学生参赛，估计该校参赛学生成绩不低于70分的人数．

查看试题解析
21. 如图，正方形 $A B C D$ 的边长为4，点 $E$ 是 $D C$ 的中点，点 $F$ 是 $A C$ 上的一动点．

(1)、当 $E F$ ∥ $A D$ 时， $D F$ = ；

(2)、求 $D F + F E$ 的最小值．

查看试题解析
22. 问题：探究函数 $y = 3 - | x |$ 的图象及其性质．
小华根据学习函数的经验，对函数 $y = 3 - | x |$ 的图象及其性质进行了探究；下面是小华的探究过程，请补充完整：

(1)、在 $y = 3 - | x |$ 的中，自变量 $x$ 可以是任意实数；下表是 $y$ 与 $x$ 的几组对应值：
x
…
-4
-3
-2
-1
0
1
2
3
4
…
y
…
-1
0
1
2
3
2
1
0
m
…
则 $m$ =；若 $A (n ， - 9) ， B (12 ， - 9)$ 为该函数图象上不同的两点，则 $n$ = ．

(2)、如图，在平面直角坐标系 $x O y$ 中，描出上表中各对对应值为坐标的点，并根据描出的点，画出该函数的图象；

(3)、根据函数图象可得该函数的最大值为，函数 $y = 3 - | x |$ 的图象与直线 $y = \frac{3}{5} x + \frac{7}{5}$ 围成的图形面积是．

查看试题解析
23. 如图，在△ $A B C$ 中， $∠ B A C = 9 0^{∘}$ ， $A D$ 是 $B C$ 边上的中线，点 $E$ 是 $A D$ 的中点，过点 $A$ 作 $A F$ ∥ $B C$ 交 $B E$ 的延长线于点 $F$ ，连接 $C F ， D F$ ．

(1)、求证：四边形 $A D C F$ 是菱形；

(2)、若 $A B = 6 c m$ ， △ $A C F$ 的面积为 $12 c m^{2}$ ，求 $A D$ 的长．

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，已知平行四边形 $O A B C$ 的顶点 $O$ 为坐标原点，顶点 $A$ 在 $x$ 轴的正半轴上， $B ， C$ 在第一象限内， $P (0 ， - 1)$ ，且 $O A = 4 ， O C = 2 \sqrt{2} ， ∠ A O C = 4 5^{∘}$ ．

(1)、顶点 $C$ 的坐标为，顶点 $B$ 的坐标为；

(2)、如图2，若直线 $l ： y = k x + b$ 过点 $P$ ，且把平行四边形 $O A B C$ 的面积分成 $1 ： 2$ 的两部分，求直线 $l$ 的函数解析式；

(3)、如图3，设对角线 $A C ， O B$ 交于点 $E$ ，在 $x$ 轴上，有一个长为1个单位长度的可以左右平移的线段 $M N$ ，点 $M$ 在点 $N$ 的左侧，连接 $P M ， E N$ ，则 $P M + E N$ 的最小值为．

查看试题解析

人员	甲	乙	丙	丁
平均数	81	86	86	82
方差	40	45	55	59

销售额（万元）	1	2	3	11
电商（家）	1	4	3	2

x	…	-4	-3	-2	-1	0	1	2	3	4	…
y	…	-1	0	1	2	3	2	1	0	m	…