陕西省渭南市韩城市2021-2022学年高二下学期理数期末考试试卷
试卷更新日期:2022-08-11 类型:期末考试
一、单选题
-
1. 若函数在处的导数为2,则( )A、2 B、1 C、 D、62. 已知函数 , 则( )A、-π B、0 C、π D、13. 若复数为纯虚数,则实数( )A、-7 B、-5 C、7 D、54. 设函数 在定义域内可导, 的图象如图所示,则导函数 的图象可能为( )
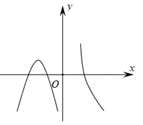 A、
A、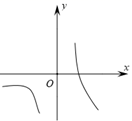 B、
B、 C、
C、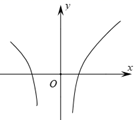 D、
D、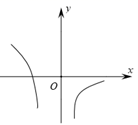 5. 随机变量服从二项分布 , 且 , , 则等于( )A、 B、 C、 D、6. 复数 , 则z的模为( )A、 B、 C、 D、27. 某电视台的一个综艺栏目对六个不同的节目排演出顺序,最前只能排甲或乙,最后不能排甲,则不同的排法共有( )
5. 随机变量服从二项分布 , 且 , , 则等于( )A、 B、 C、 D、6. 复数 , 则z的模为( )A、 B、 C、 D、27. 某电视台的一个综艺栏目对六个不同的节目排演出顺序,最前只能排甲或乙,最后不能排甲,则不同的排法共有( )
A、240种 B、288种 C、192种 D、216种8. 已知 ,复数 的共轭复数 在复平面内对应的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )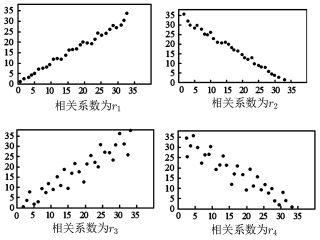 A、 B、 C、 D、10. 已知实数 , 则下列不等关系中错误的是( )A、 B、 C、 D、11. 设某车间的A类零件的质量m(单位: )服从正态分布 ,且 .若从A类零件中随机选取100个,则零件质量在 的个数大约为( )A、40 B、30 C、60 D、2412. 已知函数 , , 若存在 , 对任意 , 都有 , 则实数的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知实数 , 则下列不等关系中错误的是( )A、 B、 C、 D、11. 设某车间的A类零件的质量m(单位: )服从正态分布 ,且 .若从A类零件中随机选取100个,则零件质量在 的个数大约为( )A、40 B、30 C、60 D、2412. 已知函数 , , 若存在 , 对任意 , 都有 , 则实数的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 的展开式中的系数是 . (用数字作答)14. 曲线在点处的切线方程为.15. 一家商场在举办抽奖活动,在抽奖箱中,一共有10张奖券,其中有4张“中奖”奖券,甲乙两人先后参加抽奖活动,每人从中不放回地抽取一张奖券,甲先抽,乙后抽,则在甲中奖的条件下,乙没有中奖的概率为.16. 设函数f(x)在R上满足f(x)+xf′(x)>0,若a=(30.3)f(30.3),b=(logπ3)·f(logπ3),则a与b的大小关系为 .
三、解答题
-
17. 已知函数的定义域为R.(1)、当时,求不等式的解集;(2)、若关于x的不等式恒成立,求实数的取值范围.18. 青少年近视问题已经成为我国面临的重要社会问题.对于这一问题,习近平总书记连续作出重要指示,要求“全社会都要行动起来,共同呵护好孩子的眼睛,让他们拥有一个光明的未来”.某机构为了解使用电子产品对青少年视力的影响,随机抽取了200名青少年,调查他们每天使用电子产品的时间(单位:分钟),根据调查数据按 , , , , , 分成6组,得到如下频数分布表:
时间/分钟
频数
12
38
72
46
22
10
记每天使用电子产品的时间超过60分钟为长时间使用电子产品.
附: , 其中 .
0.10
0.05
0.010
0.001
2.706
3.841
6.635
10.828
(1)、完成下面的列联表;非长时间使用电子产品
长时间使用电子产品
合计
患近视人数
100
未患近视人数
80
合计
200
(2)、判断是否有99.9%的把握认为患近视与每天长时间使用电子产品有关.19. 某中学将要举行校园歌手大赛,现有4男3女参加,需要安排他们的出场顺序.(结果用数字作答)(1)、如果3个女生都不相邻,那么有多少种不同的出场顺序?(2)、如果3位女生都相邻,且男生甲不在第一个出场,那么有多少种不同的出场顺序?20. 已知函数(其中).(1)、求函数的极值点;(2)、若函数有三个零点,求实数的取值范围.