四川省广元市青川县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-08-11 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，四个图标中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 科技不断发展，晶体管长度越造越短，长度只有0.000000006米的晶体管已经诞生，该数用科学记数法表示为（）米．

A、 $0.6 \times 1 0^{- 9}$ B、 $6 \times 1 0^{- 8}$ C、 $60 \times 1 0^{- 9}$ D、 $6 \times 1 0^{- 9}$

查看试题解析
3. 若 $x^{2} + 2 (m - 3) x + 16$ 是完全平方式，则m的值等于（）

A、3 B、7或－1 C、7 D、－5

查看试题解析
4. 下列计算结果正确的有（）
① $\frac{3 x}{x^{2}} · \frac{x}{3 x} = \frac{1}{x}$ ；② $8 a^{2} b^{2} \cdot (- \frac{3 a}{4 b^{2}}) = - 6 a^{3}$ ；③ $\frac{a}{a^{2} - 1} \div \frac{a^{2}}{a^{2} + a} = \frac{1}{a - 1}$ ；④ $a \div b · \frac{1}{a} = a$

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 若关于 $x$ 的分式方程 $\frac{x}{x - 2} = 2 - \frac{m}{2 - x}$ 的解为正数，则满足条件的正整数 $m$ 的值为（）

A、 $1, 2, 3$ B、 $1, 2$ C、 $2, 3$ D、 $1, 3$

查看试题解析
6. 已知x+ $\frac{1}{x}$ = $\sqrt{7}$ ，则x- $\frac{1}{x}$ 的值为（　　）

A、 $\sqrt{3}$ B、±2 C、± $\sqrt{3}$ D、 $\sqrt{7}$

查看试题解析
7. 精元电子厂准备生产5400套电子元件，甲车间独立生产一半后，由于要尽快投入市场，乙车间也加入了该电子元件的生产，若乙车间每天生产的电子元件套数是甲车间的1.5倍，结果用30天完成任务，问甲车间每天生产电子元件多少套？在这个问题中设甲车间每天生产电子元件x套，根据题意可得方程为（）

A、 $\frac{2700}{x} + \frac{2700}{1.5 x} = 30$ B、 $\frac{2700}{x} + \frac{2700}{x + 1.5 x} = 30$ C、 $\frac{2700}{x} + \frac{5400}{x + 1.5 x} = 30$ D、 $\frac{5400}{x} + \frac{2700}{x + 1.5 x} = 30$

查看试题解析
8. 如图，在△ABC中，AD是角平分线，DE⊥AB于点E，△ABC的面积为15， $A B = 6$ ， $D E = 3$ ，则AC的长是（）

A、8 B、6 C、5 D、4

查看试题解析
9. 如图所示，在四边形ABCD中， $A D = 2$ ， $∠ A = ∠ D = 90 °$ ， $∠ B = 60 °$ ， $B C = 2 C D$ ，在AD上找一点P，使 $P C + P B$ 的值最小；则 $P C + P B$ 的最小值为（）

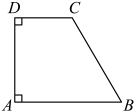A、4 B、3 C、5 D、6

查看试题解析
10. 如图，在△ABC中， $∠ B A C = 45 °$ ， AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，且 $E H = E B$ ．下列四个结论：① $∠ A B C = 45 °$ ；② $A H = B C$ ；③ $B E + C H = A E$ ；④△AEC是等腰直角三角形．你认为正确的序号是（）

A、②④ B、①②③ C、②③④ D、①②③④

查看试题解析

二、填空题

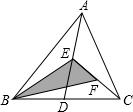
11. 已知 $2^{m} = a$ ， $2^{n} = b$ ， m，n为正整数，则 $2^{3 m + 4 n} =$ ．

查看试题解析
12. 在实数范围内分解因式： $2 a^{3} - 4 a$ ＝．

查看试题解析
13. 若 $2 x + m$ 与 $x + 2$ 的乘积中不含 $x$ 的一次项，则 $m$ 的值为．

查看试题解析
14. 如果一个多边形的内角和为1260°，那么这个多边形共有条对角线．

查看试题解析
15. 如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且 $S_{△ A B C} = 4 c m^{2}$ ，则 $S_{阴影} =$ ．

查看试题解析
16. 如图，在第一个 $△ A B A_{1}$ 中， $∠ B = 20 °$ ， $A B = A_{1} B$ ，在 $A_{1} B$ 上取一点C，延长 $A A_{1}$ 到 $A_{2}$ ，使得 $A_{1} A_{2} = A_{1} C$ ，得到第二个 $△ A_{1} A_{2} C$ ；在 $A_{2} C$ 上取一点D，延长 $A_{1} A_{2}$ 到 $A_{n}$ ，使得 $A_{2} A_{3} = A_{2} D$ ；…，按此做法进行下去，则第5个三角形中，以点 $A_{4}$ 为顶点的底角的度数为．

查看试题解析

三、解答题

17.

(1)、计算： $- 4^{2} + {(- 1)}^{2021} + | - 3 | + 3 {(π - 3)}^{0} - \sqrt{9} + {(\frac{1}{3})}^{- 2}$

(2)、解方程： $\frac{x + 4}{x - 4} - \frac{6}{x + 4} = 1$ ．

查看试题解析
18. 先化简，再求值．
$[(x + 3 y) (x - 3 y) + (2 y - x)^{2} + 5 y^{2} (1 - x) - (2 x^{2} - x^{2} y)] \div (- \frac{1}{2} x y)$ ，其中 $x = 95$ ， $y = 220$ ．

查看试题解析
19. 若x，y是等腰三角形的两条边，且满足 $4 x^{2} + 17 y^{2} - 16 x y - 4 y + 4 = 0$ ，求△ABC的周长．

查看试题解析
20. 如图1，有A型、B型正方形卡片和C型长方形卡片各若干张．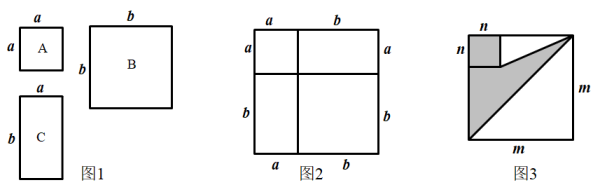

(1)、用1张A型卡片，1张B型卡片，2张C型卡片拼成一个正方形，如图2，用两种方法计算这个正方形面积，可以得到一个等式，请你写出这个等式；

(2)、选取1张A型卡片，10张C型卡片，张B型卡片，可以拼成一个正方形，这个正方形的边长用含a，b的代数式表示为；

(3)、如图3，两个正方形边长分别为m、n，m+n=10，mn=19，求阴影部分的面积．

查看试题解析
21. 如图在平面直角坐标系中， $Δ A B C$ 各顶点的坐标分别为： $A (4 ， 0)$ ， $B (- 1 ， 4)$ ， $C (- 3 ， 1)$

(1)、在图中作△ $A^{'} B^{'} C^{'}$ ，使△ $A^{'} B^{'} C^{'}$ 和 $Δ A B C$ 关于 $x$ 轴对称；

(2)、写出点 $A ′$ ， $B ′$ ， $C^{'}$ 的坐标；

(3)、求 $Δ A B C$ 的面积．

查看试题解析
22. 如图，在△ABC中， $A B = A C$ ， D、E是△ABC内的两点，AD平分∠BAC， $∠ E B C = ∠ E = 60 °$ ．若 $B E = 6 c m$ ， $D E = 2 c m$ ，求BC的长．

查看试题解析
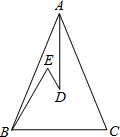23. 从三个代数式：① $a^{2} - 2 a b + b^{2}$ ， ② $3 a - 3 b$ ， ③ $a^{2} - b^{2}$ 中任选两个分别作为分式的分子和分母：

(1)、一共能得到多少个不同的分式？写出它们．

(2)、上述分式化简后，结果为整式的有哪些？写出其化简过程及结果．

查看试题解析
24. 如图，在△ABC中， $∠ B = ∠ C$ ，点D、E、F分别在AB、BC、AC边上，且 $B E = C F$ ， $A D + E C = A B$ ．

(1)、试说明： $D E = E F$ ；

(2)、当 $∠ A = 40 °$ 时，求∠DEF的度数；

(3)、猜想：写出当∠A为多少度时， $∠ E D F + ∠ E F D = 120 °$ ．

查看试题解析
25. 今年我县蜂蜜产销红火，一上市，山珍店的李老板用2400元购进第一批蜂蜜，很快售完；后又用5000元购进第二批蜂蜜，所购罐数是第一批的2倍，但进价比第一批每罐多了5元．

(1)、第一批蜂蜜每罐进价多少元？

(2)、李老板以每罐150元的价格销售第二批蜂蜜，售出80%后，为了尽快售完，决定打折促销，要使第二批蜂蜜的销售利润不少于640元，剩余的蜂蜜每罐售价最少打几折？

查看试题解析
26. 已知两个全等的等腰直角△ABC、△DEF，其中 $∠ A C B = ∠ D F E = 90 °$ ， E为AB中点，△DEF可绕顶点E旋转，线段DE，EF分别交线段CA，CB（或它们所在直线）于M、N．

(1)、如图1，当线段EF经过△ABC的顶点C时，点N与点C重合，线段DE交AC于M，求证： $A M = M C$ ；

(2)、如图2，当线段EF与线段BC边交于N点，线段DE与线段AC交于M点，连MN，EC，请探究AM，MN，CN之间的等量关系，并说明理由；

(3)、如图3，当线段EF与BC延长线交于N点，线段DE与线段AC交于M点，连MN，EC，请猜想AM，MN，CN之间的等量关系，不必说明理由．

查看试题解析