四川省甘孜藏族自治州2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-08-11 类型:期末考试
一、单选题
-
1. 观察下面图案,在A,B,C,D四幅图案中,能通过图1平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如果大于 , 那么的取值范围是( )A、 B、 C、 D、3. 都是实数,且 , 则下列不等式的变形正确的是( )A、 B、 C、 D、4. 把多项式分解因式,结果正确的是( ).A、 B、 C、 D、5. 如图,在平面直角坐标系中,点A的坐标为 , 将线段OA绕点顺时针旋转180°得到线段 , 则点的坐标是( ).
2. 如果大于 , 那么的取值范围是( )A、 B、 C、 D、3. 都是实数,且 , 则下列不等式的变形正确的是( )A、 B、 C、 D、4. 把多项式分解因式,结果正确的是( ).A、 B、 C、 D、5. 如图,在平面直角坐标系中,点A的坐标为 , 将线段OA绕点顺时针旋转180°得到线段 , 则点的坐标是( ). A、 B、 C、 D、6.
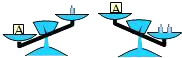
A、 B、 C、 D、6.如图天平右盘中的每个砝码的质量都是1g,则物体A的质量m(g)的取值范围在数轴上可表示为( )
 A、
A、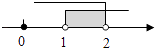 B、
B、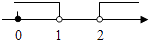 C、
C、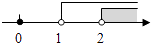 D、
D、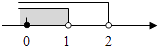 7. 用适当的符号表示 “ 的 2 倍加上 5 不大于的 3 倍减去4?”, 正确的是( )A、 B、 C、 D、8. 平行四边形 中,的度数之比有可能是( )A、 B、 C、 D、 9. 把分式中的x,y都扩大到原来的5倍,则分式的值( )A、扩大到原来的5倍 B、不变 C、缩小到原来 D、扩大到原来的25倍10. 如果不等式组无解,则的取值范围是( )A、 B、 C、 D、
7. 用适当的符号表示 “ 的 2 倍加上 5 不大于的 3 倍减去4?”, 正确的是( )A、 B、 C、 D、8. 平行四边形 中,的度数之比有可能是( )A、 B、 C、 D、 9. 把分式中的x,y都扩大到原来的5倍,则分式的值( )A、扩大到原来的5倍 B、不变 C、缩小到原来 D、扩大到原来的25倍10. 如果不等式组无解,则的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 当x=时,分式 值为0.12. 平面直角坐标系中,将点向右平移 3 个单位长度得到点 , 则点的坐标为13. 如图, 在 中, 边的垂直平分线分别交于点 , 边的垂直平 分线分别交于点 , 若 , 则的周长为
 14. 已知 中,是上一点, , , 垂足是 , 是的中点, , 则长为
14. 已知 中,是上一点, , , 垂足是 , 是的中点, , 则长为 15. 若分式方程 有增根, 则16. 已知 , 则的值是17. 如图在平行四边形中,如果 , , 的平分线交于点 , 交的延长线于点 , 则 .
15. 若分式方程 有增根, 则16. 已知 , 则的值是17. 如图在平行四边形中,如果 , , 的平分线交于点 , 交的延长线于点 , 则 . 18. 已知一个多边形的内角和再加上一个外角共 , 则这个多边形的边数是19. 如图, 在直角中, , 以直角顶点为旋转中心, 将旋转到的位置, 其中分别是的对应点, 且点在斜边上, 直角边 交于点 , 这时的度数是
18. 已知一个多边形的内角和再加上一个外角共 , 则这个多边形的边数是19. 如图, 在直角中, , 以直角顶点为旋转中心, 将旋转到的位置, 其中分别是的对应点, 且点在斜边上, 直角边 交于点 , 这时的度数是
三、解答题
-
20. 计算(1)、因式分解:(2)、解不等式组21. 解分式方程∶22. 先化简, 再求值∶ , 其中23. 如图,已知中, , 以为圆心,任意长为半径画弧交边 , AC于点和 , 再分别以为圆心,大于的长为半径画弧,两弧交于点 , 连 结并延长交于点 .
 (1)、求证: 点在线段的垂直平分线上;(2)、若 的面积为3,求的面积.24. 如图, 方格纸中每个小正方形的边长都是1个单位长度, 在方格纸中建立如图所示的 平面直角坐标系, 的顶点都在格点上, 且三个顶点的坐标分别为、
(1)、求证: 点在线段的垂直平分线上;(2)、若 的面积为3,求的面积.24. 如图, 方格纸中每个小正方形的边长都是1个单位长度, 在方格纸中建立如图所示的 平面直角坐标系, 的顶点都在格点上, 且三个顶点的坐标分别为、
⑴将先向上平移1个单位, 再向右平移4个单位后得到, 请画出, 并写出点的对应点的坐标;
⑵请画出以原点为旋转中心, 逆时针旋转所得的, 并写出 点的对应点的坐标
25. 如图, 平行四边形 的周长为36,BD=12,点是对角线AC、BD的交点,点是边的中点,点交的延长线于 . (1)、求证:四边形OCFE是平行四边形;(2)、求△DOE的周长.26. 为了满足市民的物质需求,某超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
(1)、求证:四边形OCFE是平行四边形;(2)、求△DOE的周长.26. 为了满足市民的物质需求,某超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:甲
乙
进价(元/袋)
售价(价/袋)
20
13
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)、求的值;(2)、要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价﹣进价)不少于5200元,问至少购进甲种袋装食品多少袋?
