江苏省扬州市广陵区2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-08-11 类型:期末考试
一、单选题
-
1. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是中心对称图形的是( )A、
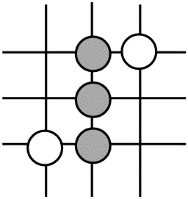
B、
B、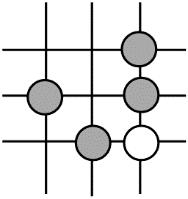
C、
C、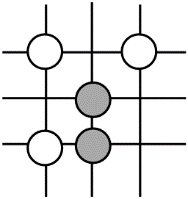
D、
D、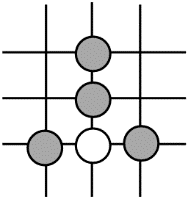
2. 下列说法正确的是( )A、想了解昆明市城镇居民人均年收入水平,应采用全面调查 B、要反映昆明市某周大气中的变化情况,宜采用扇形统计图 C、“某彩票中奖率为1%”可以理解为买张该彩票也可能中奖 D、画“任意一个矩形,是中心对称图形”,这一事件是随机事件3. 下面性质中矩形具有而菱形没有的是( )A、对角线相等 B、邻边相等 C、对角线垂直 D、对边相等4. 为了解某市2021年10000名考生的数学中考成绩,从中抽取了200名考生的成绩进行统计,在这个问题中,下列说法:①这10000名考生的数学中考成绩的全体是总体;②每个考生是个体;③从中抽取的200名考生的数学中考成绩是总体的一个样本;④样本容量是200名.其中说法正确的是( )A、①③ B、①④ C、②③ D、②④5. 下列分式从左到右变形错误的是( )A、 B、 C、 D、6. 化简二次根式的结果为( )A、 B、 C、 D、7. 已知反比例函数 , 下列结论中不正确的是( )A、其图象经过点 B、其图象分别位于第一、第三象限 C、当时, D、当时,随的增大而增大8. 用三个不等式 , , 中的两个不等式作为题设,余下的一个不等式作为结论组成一个命题,组成真命题的个数为( )A、0 B、1 C、2 D、3
2. 下列说法正确的是( )A、想了解昆明市城镇居民人均年收入水平,应采用全面调查 B、要反映昆明市某周大气中的变化情况,宜采用扇形统计图 C、“某彩票中奖率为1%”可以理解为买张该彩票也可能中奖 D、画“任意一个矩形,是中心对称图形”,这一事件是随机事件3. 下面性质中矩形具有而菱形没有的是( )A、对角线相等 B、邻边相等 C、对角线垂直 D、对边相等4. 为了解某市2021年10000名考生的数学中考成绩,从中抽取了200名考生的成绩进行统计,在这个问题中,下列说法:①这10000名考生的数学中考成绩的全体是总体;②每个考生是个体;③从中抽取的200名考生的数学中考成绩是总体的一个样本;④样本容量是200名.其中说法正确的是( )A、①③ B、①④ C、②③ D、②④5. 下列分式从左到右变形错误的是( )A、 B、 C、 D、6. 化简二次根式的结果为( )A、 B、 C、 D、7. 已知反比例函数 , 下列结论中不正确的是( )A、其图象经过点 B、其图象分别位于第一、第三象限 C、当时, D、当时,随的增大而增大8. 用三个不等式 , , 中的两个不等式作为题设,余下的一个不等式作为结论组成一个命题,组成真命题的个数为( )A、0 B、1 C、2 D、3二、填空题
-
9. 若代数式 在实数范围内有意义,则x的取值范围是。10. 转动如图的转盘(转盘中各个扇形的面积都相等),当它停止转动时,指针指向标有数字的区域的可能性最小.
 11. 计算的结果是 .12. 如图,矩形ABCD的对角线AC、BD相交于点O,∠BOC=120°,AC=6.则AB= .
11. 计算的结果是 .12. 如图,矩形ABCD的对角线AC、BD相交于点O,∠BOC=120°,AC=6.则AB= . 13. 点A(1,y1),B(3,y2)是反比例函数图象上的两点,那么y1 , y2的大小关系是y1y2 . (填“>”或“<”)14. 当时,化简代数式= .15. 若关于x的方程=1有增根,则a= .16. 如图,在△ABC中,∠ACB=90°,E,F,D分别是AB,BC,CA的中点,若CE=5,则线段DF的长是 .
13. 点A(1,y1),B(3,y2)是反比例函数图象上的两点,那么y1 , y2的大小关系是y1y2 . (填“>”或“<”)14. 当时,化简代数式= .15. 若关于x的方程=1有增根,则a= .16. 如图,在△ABC中,∠ACB=90°,E,F,D分别是AB,BC,CA的中点,若CE=5,则线段DF的长是 . 17. 如图,点A是反比例函数上的一点,过点A作轴,垂足为点C,交反比例函数的图象于点B,点P是x轴上的动点,则的面积为 .
17. 如图,点A是反比例函数上的一点,过点A作轴,垂足为点C,交反比例函数的图象于点B,点P是x轴上的动点,则的面积为 . 18. 如图,在菱形ABCD中,AB=AC=10,对角线AC、BD相交于点O,点M在线段AC上,且AM=3,点P为线段BD上的一个动点,则MP+PB的最小值是 .
18. 如图,在菱形ABCD中,AB=AC=10,对角线AC、BD相交于点O,点M在线段AC上,且AM=3,点P为线段BD上的一个动点,则MP+PB的最小值是 .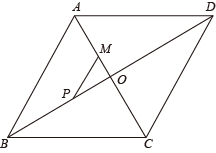
三、解答题
-
19.(1)、计算: .(2)、化简: .20. 解方程(1)、(2)、21. 在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数n
1000
2000
3000
5000
8000
10000
摸到黑球的次数m
650
1180
1890
3100
4820
6013
摸到黑球的频率
0.65
0.59
0.63
0.62
0.6025
0.6013
(1)、请估计:当n很大时,摸到黑球的频率将会接近(精确到0.1);(2)、试估计袋子中有黑球个;(3)、若学习小组通过试验结果,想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%,则可以在袋子中增加相同的白球个或减少黑球个.22. 2021年12月9日,神舟十三号乘组三位航天员首次在中国空间站进行太空授课,传播载人航天知识.某校为了了解本校学生对航天科技的关注程度,组织全校共600名学生进行了一次科普知识竞赛.为了了解本次竞赛学生的成绩分布情况,随机抽取了其中部分同学的成绩作为样本进行统计,将竞赛成绩(得分取整数)整理后分成四组,并制作了如下两个不完整的统计图,请根据所给信息,解答下列问题:
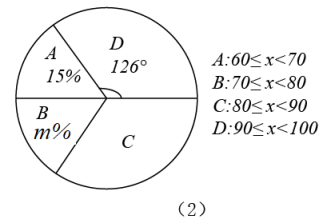 (1)、所抽取的学生数量为人,m=;(2)、求成绩为这一组所在的扇形的圆心角度数;(3)、请补全频数直方图;(4)、若成绩不低于80分为“良好”等级,则全校参加这次竞赛的学生中属于“良好”等级的约有多少人?23. 如图,在平面直角坐标系中,△ABC和△A1B1C1 关于点E成中心对称.
(1)、所抽取的学生数量为人,m=;(2)、求成绩为这一组所在的扇形的圆心角度数;(3)、请补全频数直方图;(4)、若成绩不低于80分为“良好”等级,则全校参加这次竞赛的学生中属于“良好”等级的约有多少人?23. 如图,在平面直角坐标系中,△ABC和△A1B1C1 关于点E成中心对称.
⑴画出对称中心E,并写出点E的坐标 ▲ ;
⑵画出△A1B1C1绕点O逆时针旋转90°后的△A2B2C2;
⑶画出与△A1B1C1关于点O成中心对称的△A3B3C3.
24. 如图,在平面直角坐标系中,一次函数y1=kx+b的图象与反比例函数y2=(m>0)的图象交于点A(2,5),B(﹣5,n).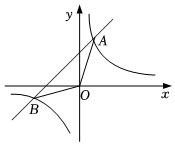 (1)、分别求出两个函数的解析式;(2)、求OAB的面积;(3)、根据图象,直接写出关于x的不等式kx+b≤的解集.25. 用分式方程解决问题:某商店用6000元购进A款篮球,用5400元购进B款篮球,B款每个篮球的进价是A款每个篮球进价的1.2倍,B款篮球的数量比A款篮球的数量少15个.问两款篮球每个的进价各是多少元.26. 在矩形ABCD中,连接AC,AC的垂直平分线交AC于点O,分别交AD、BC于点E、F,连接CE和AF.
(1)、分别求出两个函数的解析式;(2)、求OAB的面积;(3)、根据图象,直接写出关于x的不等式kx+b≤的解集.25. 用分式方程解决问题:某商店用6000元购进A款篮球,用5400元购进B款篮球,B款每个篮球的进价是A款每个篮球进价的1.2倍,B款篮球的数量比A款篮球的数量少15个.问两款篮球每个的进价各是多少元.26. 在矩形ABCD中,连接AC,AC的垂直平分线交AC于点O,分别交AD、BC于点E、F,连接CE和AF.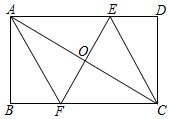 (1)、求证:四边形AECF为菱形;(2)、若AB=4,BC=8,求菱形AECF的面积.27. 我们要学会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界.例如生活经验:(1)、往一杯糖水中再加入一点糖,糖水就变甜了.这一生活经验可以转译成数学问题:a克糖放入水中,得到b克糖水,此时糖水的含糖量我们可以记为(b>a>0),再往杯中加入m(m>0)克糖,此时糖水的含糖量变大了,
(1)、求证:四边形AECF为菱形;(2)、若AB=4,BC=8,求菱形AECF的面积.27. 我们要学会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界.例如生活经验:(1)、往一杯糖水中再加入一点糖,糖水就变甜了.这一生活经验可以转译成数学问题:a克糖放入水中,得到b克糖水,此时糖水的含糖量我们可以记为(b>a>0),再往杯中加入m(m>0)克糖,此时糖水的含糖量变大了,①用数学关系式可以表示为 ▲ ;
A. B. C.
②请证明你选择的数学关系式是正确的.
(2)、再如:矩形的面积为S(S为定值),设矩形的长为x,则宽为 , 周长为2 , 当矩形为正方形时,周长为 , “在面积一定的矩形中,正方形的周长最短”这一结论,①用数学关系式可以表示为 ▲ ;
A. B. C.
②请证明你选择的数学关系式是正确的.(友情提示: , )
28. 问题情境:如图①,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE′(点A的对应点为点C).延长AE交CE′于点F,连接DE.
 (1)、猜想证明:
(1)、猜想证明:试判断四边形BE'FE的形状,并说明理由;
(2)、如图②,若DA=DE,请猜想线段CF与的数量关系并加以证明;(3)、解决问题:如图①,若AB=4,当BE的长为时,△ADE为等腰三角形,请直接写出结果.