广西壮族自治区钦州市2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-11 类型：期末考试

进入出卷网下载

一、单选题

1. 直角三角形的两条直角边分别为6，8，则该直角三角形的斜边长为（）

A、4 B、 $2 \sqrt{7}$ C、10 D、12

查看试题解析
2. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{3}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{8}$ D、 $\sqrt{9}$

查看试题解析
3. 某班10名学生的体育测试成绩分别为（单位：分）57，58.56，54，58，60，58，57，56，57，则这组数据的众数是（）

A、57 B、58 C、60 D、57，58

查看试题解析
4. 在平面直角坐标系中，将函数y＝6x＋3的图象向下平移2个单位长度，平移后的图象与y轴的交点坐标为（）

A、（0，1） B、（1，0） C、 $(- \frac{1}{6} ， 0)$ D、 $(0 ， - \frac{1}{6})$

查看试题解析
5. 由下列线段a，b，c不能组成直角三角形的是（）

A、a＝3，b＝4，c＝5 B、a＝2， $b = 2 \sqrt{3}$ ， c＝3 C、a＝5，b＝12，c＝13 D、a＝1，b＝2， $c = \sqrt{3}$

查看试题解析
6. 平行四边形ABCD中，∠C：∠D＝4：5，则∠D的度数是（）

A、60° B、90° C、100° D、120°

查看试题解析
7. 代数式 $\frac{1}{\sqrt{x + 2}}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x \neq 0$ B、 $x \neq - 2$ C、x>－2 D、 $x \geq - 2$

查看试题解析
8. 如图，在矩形AOBD中，点D的坐标是（1，3），则AB的长为（）

A、3 B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、 $\sqrt{10}$

查看试题解析
9. 下列计算正确的是（）

A、 ${(- \sqrt{3})}^{2} = 3$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 $\sqrt{\frac{1}{2}} = 2 \sqrt{2}$ D、 $3 \sqrt{2} = \sqrt{3 \times 2}$

查看试题解析
10. 若正比例函数y＝(3＋k)x的图象经过点 $A (x_{1} ， y_{1})$ 和点 $B (x_{2} ， y_{2})$ ，当 $x_{1} < x_{2}$ 时， $y_{1} > y_{2}$ ，则k的取值范围是（）

A、 $k > 0$ B、 $k < 0$ C、 $k > - 3$ D、 $k < - 3$

查看试题解析
11. 如图，在平面直角坐标系中，菱形ABCD的边长为6，它的一边AB在x轴上，且AB的中点是坐标原点O，点D在y轴正半轴上，则点C的坐标为（）

A、 $(3 \sqrt{3} ， 3)$ B、 $(3 ， 3 \sqrt{3})$ C、 $(6 ， 3 \sqrt{3})$ D、 $(3 \sqrt{3} ， 6)$

查看试题解析
12. 如图，已知一次函数y＝kx+2的图象与x轴，y轴分别交于点A，B，与正比例函数y＝ $\frac{1}{3}$ x交于点C，已知点C的横坐标为2，下列结论：①关于x的方程kx+2＝0的解为x＝3；②对于直线y＝kx+2，当x＜3时，y＞0；③对于直线y＝kx+2，当x＞0时，y＞2；④方程组 ${\begin{array}{l} 3 y - x = 0 \\ y - k x = 2 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = \frac{2}{3} \end{array}$ ，其中正确的是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题

13. 若四个数据4，5，x，6的平均数是5，那么x的值是．

查看试题解析
14. 若一次函数y＝mx＋3的图象经过点（2，7），则m的值是．

查看试题解析
15. 已知长方形的长和宽分别为 $\sqrt{8}$ ， $\sqrt{2}$ ，则它的周长=.

查看试题解析
16. 如图，在 $R t △ A B C$ 中，∠ACB＝90°，AC＝3，BC＝4，点D为AB的中点，则线段CD的长为．

查看试题解析
17. 如图，图1中是第七届国际数学教育大会（ICME－7）会徽图案、它是由一串有公共顶点O的直角三角形（如图2）演化而成的．如果图2中的 $O A_{1} = A_{1} A_{2} = A_{2} A_{3} = \cdot \cdot \cdot \cdot \cdot \cdot = A_{7} A_{8} = 1$ ，若 $S_{1}$ 代表 $△ A_{1} O A_{2}$ 的面积， $S_{2}$ 代表 $△ A_{1} O A_{2}$ 的面积，以此类推， $S_{2}$ 代表 $△ A_{7} O A_{8}$ 的面则 $S_{1}^{2} + S_{2}^{2} + S_{3}^{2} + \cdot \cdot \cdot + S_{7}^{2}$ 的值为．

查看试题解析
18. 如图，点E，F在正方形ABCD内部且AE⊥EF，CF⊥EF，已知AE＝9，EF＝5，FC＝3，则正方形ABCD的边长为．

查看试题解析
19. 已知 $a$ ， $b$ ， $c$ 实数在数轴上的对应点如图所示，化简 $\sqrt{a^{2}} - | c - a | + \sqrt{{(b - c)}^{2}} =$ ．

查看试题解析

三、解答题

20. 计算：

(1)、 $3 \sqrt{2} + 1 - (3 \sqrt{2} - 2)$ ；

(2)、 $\sqrt{2} \times \sqrt{3} - \frac{12}{\sqrt{6}}$ ．

查看试题解析
21. 小辉与小红沿同一条路同时从学校出发到图书馆查阅资料，学校距离图书馆4千米，小辉骑自行车，小红步行，当小辉从原路返回到学校时，小红刚好到达图书馆．图中折线O－A－B－C和线段OD分别表示小辉和小红离学校的路程s（千米）与时间t（分钟）之间的函数关系.
请根据图象回答下列问题：

(1)、小辉在图书馆查阅资料的时间为分钟，小辉返回学校的速度为千米/分；

(2)、请求出小红离开学校的路程s（千米）与所经过的时间t（分钟）之间的函数关系式；

(3)、当小辉与小红迎面相遇时，他们离学校的路程是多少千米？

查看试题解析
22. 图①是某小区的一组智能通道闸机，行人在右侧刷门禁卡识别成功后，两侧的圆弧翼闸会收回到两侧闸机箱内，这时行人即可通行，图②是两圆弧翼展开时的截面图，扇形ABC和扇形DEF是闸机的“圆弧翼”，两圆弧翼成轴对称，BC和EF均垂直于地面，点A与点D在同一水平线上，且它们之间的距离为10cm，连接AD，并向两方延长，分别交BC，EF于点G，H．若 $B G = \sqrt{3} A G$ ﹐BA＝ED＝60cm，求闸机通道的宽度GH．

查看试题解析
23. 2022年3月23日，神舟十三号3名航天员在中国空间站为青少年们讲授了“天宫课堂”第二课，点燃了无数青少年心中的科学梦想．海豚学校4月份组织了首届“航天梦报国情”航天知识竞赛，八年级全体学生参加了“航天知识竞赛”，为了解本次竞赛的成绩，小军随机抽取八年级20名参赛学生的成绩（单位：分）．
收集数据：
90，75，80，80，70，75，80，85，82，95，95，75，90，70，92，95，84，75，85，67
整理数据：
成绩x/分
$60 \leq x < 70$
$70 \leq x < 80$
$80 \leq x < 90$
$90 \leq x < 100$
频数
1
6
a
b
分析数据：
平均数
中位数
众数
82
c
d
根据上述数据回答以下问题：

(1)、请直接写出表格中a，b，c，d的值：

(2)、活动组委会决定，给成绩在90分及以上的同学授予“小宇航员”称号．根据上面的统计结果，估计该校八年级1000人中约有多少人将获得“小宇航员”称号；

(3)、样本20名参赛学生中的小蕾同学成绩为83分，请你从平均数、中位数中选择一个统计量来说说小蕾的成绩如何？

查看试题解析
24. 如图，在 $△ A B C$ 中，∠ACB＝90°，AC＝BC，P是 $△ A B C$ 内一点，且PB＝1，PC＝2，PA＝3，过点C作CD⊥CP，垂足为C，令CD＝CP，连接DP，BD，求∠BPC的度数．

查看试题解析
25. 某爱心企业计划购进甲，乙两种呼吸机赠予当地医院．若购进甲种3台，乙种2台，则共需18000元；若购进甲种2台，乙种1台．则共需11000元．

(1)、求甲，乙两种呼吸机每台成本分别为多少元？

(2)、该公司决定购进甲，乙两种呼吸机共60台，且购进甲种呼吸机台数不低于乙种台数的一半，则如何购买两种机器能使花费最少？最少费用为多少？

查看试题解析
26. 人教版数学八年级下册教材的数学活动一折纸，引起许多同学的兴趣．实践发现：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开；以BM为折痕再一次折叠纸片，使点A落在折痕EF上的点N处，把纸片展开；连接AN．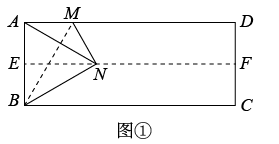

(1)、求∠MNE；

(2)、如图②，折叠矩形纸片ABCD，使点A落在BC边上点 $A^{'}$ 处，并且折痕交BC边于点T，交AD边于点S，把纸片展开，连接 $A A^{'}$ 交ST于点O，连接AT．求证：四边形 $S A T A^{'}$ 是菱形；

(3)、如图③，矩形纸片ABCD中，AB＝10，AD＝26，折叠纸片，使点A落在BC边上的点 $A^{'}$ 处，并且折痕交AB边于点T，交AD边于点S，把纸片展平，请求出线段AT的取值范围．

查看试题解析

成绩x/分	$60 \leq x < 70$	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x < 100$
频数	1	6	a	b

平均数	中位数	众数
82	c	d