广西贵港市桂平市2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-11 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点P（2，﹣3）在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列各组线段中，能构成直角三角形的是（）

A、2，3，4 B、3，4，6 C、5，12，13 D、4，6，7

查看试题解析
3. 若一个多边形的每个外角都等于60°，则它的内角和等于（）

A、180° B、720° C、1080° D、540°

查看试题解析
4. 下列条件中，不能判定平行四边形 $A B C D$ 是矩形的是（）

A、 $∠ A = ∠ C$ B、 $∠ A = ∠ B$ C、 $A C = B D$ D、 $A B ⊥ B C$

查看试题解析
5. 班级共有40名学生，在一次体育抽测中有4人不合格，那么不合格人数的频率为（）

A、0.01 B、0.1 C、0.2 D、0.5

查看试题解析
6. 下列说法中，错误的是（）

A、角平分线上的点到角两边的距离相等 B、正方形的对角线互相垂直平分 C、斜边和一锐角对应相等的两个直角三角形全等 D、如果两个三角形全等，那么这两个三角形一定成中心对称

查看试题解析
7. 在平面直角坐标系中，若点P(a－3，1)与点Q(2，b＋1)关于x轴对称，则a＋b的值是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 已知一次函数 $y = (a + 3) x + b + 1$ 的图象经过过一、二、四象限，那么 $a$ ， $b$ 的取值范围是（）

A、 $a > - 3$ ， $b > - 1$ B、 $a < - 3$ ， $b < - 1$ C、 $a > - 3$ ， $b < - 1$ D、 $a < - 3$ ， $b > - 1$

查看试题解析
9. 如图， $C D$ 是 $△ A B C$ 的中线， $∠ A C B = 90 °$ ， $∠ C D B = 100 °$ ，则 $∠ A$ 等于（）

A、 $20 °$ B、 $45 °$ C、 $50 °$ D、 $80 °$

查看试题解析
10. 如图，一次函数 $y = - \frac{3}{4} x + 3$ 的图象分别与 $x$ 轴、 $y$ 轴交于点 $A$ 、 $B$ ，以线段 $A B$ 为边在第一象限内作等腰 $R t Δ A B C$ ， $∠ B A C = 90 °$ ，则过 $B$ 、 $C$ 两点直线的解析式为（）

A、 $y = \frac{1}{7} x + 3$ B、 $y = \frac{1}{5} x + 3$ C、 $y = \frac{1}{4} x + 3$ D、 $y = \frac{1}{3} x + 3$

查看试题解析
11. 如图，在△ABC中，AC=3、AB=4、BC=5， P为BC上一动点，PG⊥AC于点G，PH⊥AB于点H，M是GH的中点，P在运动过程中PM的最小值为（）

A、2.4 B、1.4 C、1.3 D、1.2

查看试题解析
12. 如图，正方形 $A B C D$ 和正方形 $C E F G$ 中，点 $D$ 在 $C G$ 上，已知 $B C = 1$ ， $C E = 7$ ，点 $H$ 是 $A F$ 的中点，则 $C H$ 的长是（）

A、 $\sqrt{13}$ B、3.5 C、4 D、5

查看试题解析

二、填空题

13. 在 $△ A B C$ 中， $D$ 、 $E$ 分别为 $A B$ 和 $A C$ 中点，若 $B C = 6$ ，则 $D E$ 的长为．

查看试题解析
14. 《论语十则》中有句话：“知之为知之不知为不知”这句话中“知”字出现的频率为．

查看试题解析
15. 直线 $y = x + 1$ 向上平移5个单位后，得到的直线的表达式是．

查看试题解析
16. 如图，在RtΔABC中，∠ACB＝90°，AD为中线，E为AD的中点，F为BE的中点，连接DF．若AC＝4 $\sqrt{3}$ ， DF⊥BE，则DF的长为．

查看试题解析
17. 如图，将两条宽度均为2的纸条相交成 $30 °$ 角叠放，则重合部分构成的四边形 $A B C D$ 的面积为．

查看试题解析
18. 对于点P（a，b），点Q（c，d），如果a﹣b＝c﹣d，那么点P与点Q就叫作等差点．例如：点P（4，2），点Q（﹣1，﹣3），因4﹣2＝1﹣（﹣3）＝2，则点P与点Q就是等差点．如图在矩形GHMN中，点H（2，3），点N（﹣2，﹣3），MN⊥y轴，HM⊥x轴，点P是直线y＝x+b上的任意一点（点P不在矩形的边上），若矩形GHMN的边上存在两个点与点P是等差点，则b的取值范围为．

查看试题解析

三、解答题

19. 设一次函数y=kx+b（k≠0）的图象经过A（1，3）、B（0，－2）两点，求此函数的解析式．

查看试题解析
20. 已知△ABC的三边长a、b、c满足| $\frac{1}{2}$ a-4|+(2b-12)²+ $\sqrt{10 - c}$ =0，试判断△ABC的形状，并说明理由．

查看试题解析
21. 如图，已知平行四边形ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于点M、N．

(1)、求证：四边形CMAN是平行四边形．

(2)、若DM=2，AN=3，求AB的长．

查看试题解析
22. 某校为了解八年级学生的视力情况，对八年级的学生进行了一次视力抽样调查，并将调查的数据进行统计整理，绘制出如图的频数分布表和频数分布直方图．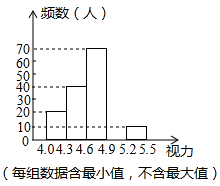
视力
频数／人
频率
$4.0 \leq x < 4.3$
20
0.1
$4.3 \leq x < 4.6$
40
0.2
$4.6 \leq x < 4.9$
80
0.4
$4.9 \leq x < 5.2$
$a$
0.25
$5.2 \leq x < 5.5$
10
$b$

(1)、在频数分布表中，则 $a =$ ， $b =$ ；

(2)、将频数分布直方图补充完整；

(3)、若视力在4.6以上（含4.6）均属正常，求视力正常的人数占被调查人数的百分比．

查看试题解析
23. 某公司到果品基地购买某种优质水果慰问医务工作者，果品基地对购买量在3000kg以上（含3000kg）的顾客采用两种销售方案．甲方案：每千克9元，由基地送货上门；乙方案：每千克8元，由顾客自己租车运回．已知该公司租车从基地到公司的运输费用为5000元．

(1)、分别写出该公司两种购买方案付款金额y（元）与所购买的水果量x（kg）之间的函数关系式，并写出自变量x的取值范围．

(2)、当购买量在哪一范围时，选择哪种购买方案付款最少？并说明理由．

查看试题解析
24. 已知：如图，边长为 $4$ 的菱形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点 $O$ ，若 $∠ C A D = ∠ D B C$ .

(1)、求证：四边形 $A B C D$ 是正方形.

(2)、 $E$ 是 $O B$ 上一点， $B E = 1$ ，且 $D H ⊥ C E$ ，垂足为 $H$ ， $D H$ 与 $O C$ 相交于点 $F$ ，求线段 $O F$ 的长.

查看试题解析
25. 如图，在平面直角坐标系中，长方形 $O A B C$ 的顶点 $A$ ， $C$ 分别在 $x$ 轴、 $y$ 轴的正半轴上，点 $B$ 的坐标为 $(8 ， 4)$ ，将该长方形沿 $O B$ 翻折，点 $A$ 的对应点为点 $D$ ， $O D$ 与 $B C$ 交于点 $E$ ．

(1)、证明： $E O = E B$ ；

(2)、求点 $E$ 的坐标；

(3)、点 $P$ 是直线 $O B$ 上的任意一点，且 $△ O P C$ 是等腰三角形，请直接写出满足条件的点 $P$ 的坐标．

查看试题解析
26. 在▱ABCD中，∠BAD的平分线交直线BC于点E，交直线DC的延长线于点F，以EC、CF为邻边作▱ECFG.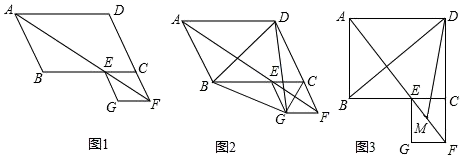

(1)、如图1，证明▱ECFG为菱形；

(2)、如图2，若∠ABC=120°，连接BG、CG，并求出∠BDG的度数：

(3)、如图3，若∠ABC=90°，AB=6，AD=8，M是EF的中点，求DM的长.

查看试题解析

视力	频数／人	频率
$4.0 \leq x < 4.3$	20	0.1
$4.3 \leq x < 4.6$	40	0.2
$4.6 \leq x < 4.9$	80	0.4
$4.9 \leq x < 5.2$	$a$	0.25
$5.2 \leq x < 5.5$	10	$b$