福建省泉州市泉港区2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-08-11 类型:期末考试
一、单选题
-
1. 化简 ,结果得( )A、x-2 B、x+2 C、 D、2. 点P(2,-3)关于x轴对称点的坐标是( )A、(-2,-3) B、(2,3) C、(-2,3) D、(-3,2)3. 将方程进行配方,下列正确的是( )A、 B、 C、 D、4. 下列图形中,不属于中心对称图形的是( )A、等边三角形 B、菱形 C、矩形 D、平行四边形5. 下列命题中,正确的是( )A、四边形的对角线相等 B、菱形的对角线互相垂直 C、平行四边形的对角线相等 D、矩形的对角线互相垂直6. 淘气统计一组数据142,140,143,136,149,139,得到它们的方差为 . 奇思将这组数据中的每一个数都减去140,得到一组新数据2,0,3,-4,9,-1,计算得出这组新数据的方差为 . 则与的关系为( )A、 B、 C、 D、7. 将直线沿x轴向左平移3个单位得到直线L,则直线L的解析式是( )A、y=2x+2 B、y=2x+8 C、y=2x-1 D、y=2x+118. 我国古代数学专著《九章算数》中有一名题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何.”其大意是:已知甲、乙二人同时从一地出发,甲的速度为7,乙的速度为3.乙向东行走,甲先向南行走10步时偏离原方向,朝北偏东的方向直行走一段后与乙相遇.问:甲、乙各行走了多少步?设、分别为甲、乙走的路程(单位:步),则( )
 A、 , B、 , C、 , D、 ,9. 函数与(k、b为常数,且kb≠0)在同坐标系内的图象大致是( )A、
A、 , B、 , C、 , D、 ,9. 函数与(k、b为常数,且kb≠0)在同坐标系内的图象大致是( )A、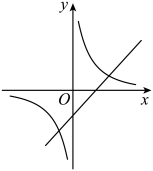 B、
B、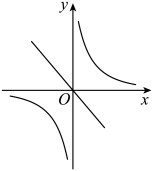 C、
C、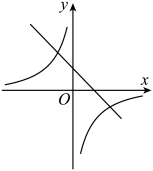 D、
D、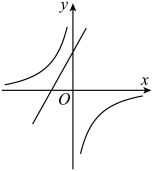 10. 已知双曲线过点、、、 , 且 . 下列结论正确的是( )A、 B、 C、 D、
10. 已知双曲线过点、、、 , 且 . 下列结论正确的是( )A、 B、 C、 D、二、填空题
-
11. 函数中,自变量x的取值范围是 .12. 计算: =.13. 如果一组数据3,7,5,x,9的众数为7,那么这组数据的中位数为 .14. 已知 , 是一元二次方程 的两根,则 .15. 如图,菱形ABCD中, , AD的垂直平分线交对角线BD于点P,垂足为N,连结CP,则∠BPC=度.
 16. 如图,在中,E点是BD的中点,MN经过E点分别与AD、BC相交于点M、N.下列四个结论:
16. 如图,在中,E点是BD的中点,MN经过E点分别与AD、BC相交于点M、N.下列四个结论:
①;②;③A、C、E三点共线;④若 , 则 . 其中正确的结论有 . (写出所有正确结论的序号)
三、解答题
-
17. 计算: .18. 如图,BD是的对角线,点E、F在BD上, . 求证: .
 19. 疫情期间,某地开展“抗击疫情·教科研在行动”中,鼓励名师率先示范,推出名师公益大课堂,为学生提供线上直播课.据统计,第一天公益课受益学生2万人次,第三天公益课受益学生2.42万人次.(1)、设第二天,第三天公益课受益学生人次的增长率相同,请求出这个增长率;(2)、若(1)中的增长率保持不变,预计第四天公益课受益学生将达到多少万人次?20. 已知关于x的一元二次方程 .(1)、当m=1时,试求出该方程的解;(2)、求证:不论m取任何值,该方程总有两个不相等的实数根.21. 如图,在中,∠BAC的角平分线交BC于点D, .
19. 疫情期间,某地开展“抗击疫情·教科研在行动”中,鼓励名师率先示范,推出名师公益大课堂,为学生提供线上直播课.据统计,第一天公益课受益学生2万人次,第三天公益课受益学生2.42万人次.(1)、设第二天,第三天公益课受益学生人次的增长率相同,请求出这个增长率;(2)、若(1)中的增长率保持不变,预计第四天公益课受益学生将达到多少万人次?20. 已知关于x的一元二次方程 .(1)、当m=1时,试求出该方程的解;(2)、求证:不论m取任何值,该方程总有两个不相等的实数根.21. 如图,在中,∠BAC的角平分线交BC于点D, . (1)、在AB上求作一点F,使得;(请保留尺规作图痕迹,不写作法)(2)、四边形AFDE是菱形吗?请说明理由.22. 在平面直角坐标系xOy中,三个顶点的坐标分别为:A(4,2)、B(3,0)、C(4,0),反比例函数的图象恰好经过AC的中点D.(1)、设直线AB与y轴的交点为P点,试求出OP的长度;(2)、已知点F与点B关于点E(2,2)对称.试判断点F是否在该反比例函数的图象上,并说明理由.23. 为了解同学的体能情况,乐乐将全班同学的3月份体育测试成绩绘制成下表(单位:分).设测试成绩为x分,当时记为A等级,时记为B等级,时记为C等级,时记为D等级.请根据表格信息,解答问题:
(1)、在AB上求作一点F,使得;(请保留尺规作图痕迹,不写作法)(2)、四边形AFDE是菱形吗?请说明理由.22. 在平面直角坐标系xOy中,三个顶点的坐标分别为:A(4,2)、B(3,0)、C(4,0),反比例函数的图象恰好经过AC的中点D.(1)、设直线AB与y轴的交点为P点,试求出OP的长度;(2)、已知点F与点B关于点E(2,2)对称.试判断点F是否在该反比例函数的图象上,并说明理由.23. 为了解同学的体能情况,乐乐将全班同学的3月份体育测试成绩绘制成下表(单位:分).设测试成绩为x分,当时记为A等级,时记为B等级,时记为C等级,时记为D等级.请根据表格信息,解答问题:66
69
77
73
72
62
79
78
66
82
86
84
83
84
86
87
89
85
86
88
91
97
91
98
90
95
96
93
92
99
(1)、试求出3月份体育测试成绩的C等级同学的平均成绩;(2)、全班同学积极响应学校号召,经过一个多月的强化训练,并参加对比式体育测试.乐乐再次统计成绩后,发现D等级的同学平均成绩提高15分,C等级的同学平均成绩提高10分,B等级的同学平均成绩提高5分,A等级的同学平均成绩提高0.9分.请求出强化训练后该班学生平均成绩所提高的分数.24. 冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”深受广大人民的喜爱,某商场准备购进“冰墩墩”和“雪容融”这两款毛绒玩具共200个.已知:每个“冰墩墩”的进价比“雪容融”的进价多20元,用3000元购进“冰墩墩”的数量与用2400元购进“雪容融”的数量相同.(1)、请求出“冰墩墩”和“雪容融”这两款毛绒玩具的进价;(2)、若该商场分别以240元、160元的单价出售“冰墩墩”和“雪容融”这两款毛绒玩具,并将这两款毛绒玩具的总利润拟定在不少于21700元,且不超过22300元之间.问该商场共有几种进货方案?(利润=售价一进价)(3)、在(2)的条件下,商场准备对“冰墩墩”毛绒玩具进行优惠促销活动,决定对“冰墩墩”毛绒玩具每个优惠a(50<a<70)元出售,“雪容融”毛绒玩具价格不变.那么该商场要获得最大利润应如何进货?25. 如图,在矩形ABCD中,连结BD,将绕点A逆时针旋转90°得 , 其中D、B的对应点分别是P、E,连结CP. (1)、若 , 求证:四边形PBDC为平行四边形;(2)、延长DB交PE于F,连结FA.
(1)、若 , 求证:四边形PBDC为平行四边形;(2)、延长DB交PE于F,连结FA.①若 , , 求FB的长;
②求证: .