四川省遂宁市2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-11 类型：期末考试

进入出卷网下载

一、单选题

1. 方程 $| x - 3 | = 2$ 的解是（）

A、 $x = 5$ B、 $x = 1$ C、 $x = 1 或 x = 5$ D、 $x = - 1 或 x = 5$

查看试题解析
2. 下列方程中，解为x=1的是（）

A、x﹣1=﹣1 B、﹣2x= $\frac{1}{2}$ C、 $\frac{1}{2}$ x=﹣2 D、2x﹣1=1

查看试题解析
3. 下列各式中是二元一次方程的是（）

A、 $x - \frac{1}{y} = 2$ B、 $x + 2 - y$ C、 $2 x y + 3 = 1$ D、 $3 x + 2 y = 1$

查看试题解析
4. 把方程 $2 x - y = 1$ 写成用含x的代数式表示y的形式是（）

A、 $y = 2 x + 1$ B、 $y = 2 x - 1$ C、 $x = \frac{y + 1}{2}$ D、 $x = \frac{y - 1}{2}$

查看试题解析
5. 下列变形中，不正确的是（）.

A、若a>b，则a+3>b+3 B、若a>b，则 $\frac{1}{3}$ a> $\frac{1}{3}$ b C、若a<b，则-a<-b D、若a<b，则-2a>-2b

查看试题解析
6. 如图，数轴上表示的解集为（）

A、﹣3＜x≤2 B、x≤2 C、x＞﹣3 D、﹣3≤x＜2

查看试题解析
7. 下列长度的三条线段，哪一组不能构成三角形（）

A、3，3，3 B、3，4，5 C、5，6，10 D、4，5，9

查看试题解析
8. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
9. 如图所示，如果将一副三角板按如图方式叠放，那么 ∠1 等于（）

A、 $120 °$ B、 $105 °$ C、 $60 °$ D、 $45 °$

查看试题解析
10. 下列方程的变形中，正确的是（）

A、方程 $3 x - 2 = 2 x + 1$ ，移项，得 $3 x - 2 x = - 1 + 2$ B、方程 $3 - x = 2 - 5 (x - 1)$ ，去括号，得 $3 - x = 2 - 5 x - 1$ C、方程 $\frac{2}{3} x = \frac{3}{2}$ ，未知数系数化为1，得 $x = 1$ D、方程 $\frac{x - 1}{2} - \frac{x}{5} = 1$ ，可化为 $5 (x - 1) - 2 x = 10$

查看试题解析
11. 已知二元一次方程组 ${\begin{array}{l} 2 a - b = 3 ， \\ a + b = 1 ， \end{array}$ 则 $3 a + 6 b =$ （）

A、6 B、4 C、3 D、2

查看试题解析
12. 如果仅用一种正多边形进行镶嵌，下列正多边形：正五边形、正方形、正六边形、正八边形、正三角形中不能构成平面镶嵌的有（　　）个．

A、2 B、3 C、4 D、5

查看试题解析
13. 如图，在△ABC中，∠1=∠2，G为AD的中点，延长BG交AC于E、 F为AB上的一点，CF⊥AD于H，下列判断正确的有（）

A、AD是△ABE的角平分线 B、BE是△ABD边AD上的中线 C、AH为△ABC的角平分线 D、CH为△ACD边AD上的高

查看试题解析
14. 一个多边形的外角和是内角和的 $\frac{2}{7}$ ，这个多边形的边数是（）

A、7 B、8 C、9 D、10

查看试题解析
15. 《九章算术》中记载了这样一个数学问题：今有甲发长安，五日至齐；乙发齐，七日至长安.今乙发已先二日，甲仍发长安.问几何日相逢？译文：甲从长安出发，5日到齐国；乙从齐国出发，7日到长安.现乙先出发2日，甲才从长安出发.问甲出发几日，甲乙相逢？设甲出发x日，甲乙相逢，可列方程（）

A、 $\frac{x + 2}{7} + \frac{x}{5} = 1$ B、 $\frac{7}{x + 2} + \frac{5}{x} = 1$ C、 $\frac{7}{x + 2} - \frac{5}{x} = 1$ D、 $\frac{x + 2}{7} = \frac{x}{5}$

查看试题解析
16. 若数a既使得关于x、y的二元一次方程组 ${\begin{array}{l} x + y = 6 \\ 3 x - 2 y = a + 3 \end{array}$ 有正整数解，又使得关于x的不等式组 ${\begin{array}{l} \frac{3 x - 5}{2} > x + a \\ \frac{3 - 2 x}{9} \leq - 3 \end{array}$ 的解集为x≥15，那么所有满足条件的a的值之和为（）

A、﹣15 B、﹣30 C、﹣10 D、0

查看试题解析

二、填空题

17. 若 $| 2 x - 3 y + 5 |$ 与 $（ 2 x + 3 y - 13 ）^{2}$ 互为相反数，则 $2 x - y$ 的值为．

查看试题解析
18. 若关于x，y的二元一次方程组 ${\begin{array}{l} 2 x + 3 y = k \\ 3 x + 2 y = k + 2 \end{array}$ 的解满足x，y互为相反数，则k的值为．

查看试题解析
19. 一个三角形的三个内角的度数的比是1:2:3，这个三角形是三角形；

查看试题解析
20. 如果过某多边形的一个顶点的对角线有6条，则该多边形一共有条对角线．

查看试题解析
21. 若关于x的不等式组 ${\begin{cases} \end{cases} \begin{array}{l} x ＞ - a - 2 \\ x ＜ 3 a + 2 \end{array}$ 无解，则a的取值范围是．

查看试题解析

三、解答题

22. 解方程组 ${\begin{array}{l} a + b + c = 6 \\ 3 a - b + c = 4 \\ 2 a + 3 b - c = 12 \end{array}$ ．

查看试题解析
23. 解方程： $\frac{x - 1}{2} = 1 - \frac{3 x + 2}{5}$ ．

查看试题解析
24. 解不等式 $3 (x + 2) - 1 \geq 5 - 2 (x - 2)$

查看试题解析
25. 解不等式组： ${\begin{array}{l} x - 3 (x - 1) \geq - 1 ① \\ \frac{x}{3} < \frac{x + 1}{2} ② \end{array}$ ，并把不等式组的解集表示在数轴上.

查看试题解析
26. 如图，在△ABC中，BE平分∠ABC交AC于点E，CD⊥AC交AB于点D，∠BCD＝∠A，求∠BEA的度数．

查看试题解析
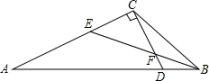27. 如图，将六边形纸片ABCDEF沿虚线剪去一个角（∠BCD）后，得到∠1+∠2+∠3+∠4+∠5＝470°．

(1)、求六边形ABCDEF的内角和；

(2)、求∠BGD的度数．

查看试题解析
28. 如图，在正方形网格中，点A、B、C、M、N都在格点上．

（1）作 $△ A B C$ 关于直线MN对称的图形 $△ A^{'} B^{'} C^{'}$ ．
（2）若网格中最小正方形的边长为2，求 $△ A B C$ 的面积．
（3）点P在直线MN上，当 $△ P A C$ 周长最小时，P点在什么位罝，在图中标出P点．

查看试题解析
29. 接种新冠病毒疫苗，建立全民免疫屏障，是战胜病毒的重要手段.北京科兴中维需运输一批疫苗到我市疾控中心，据调查得知，2辆 $A$ 型冷链运输车与3辆 $B$ 型冷链运输车一次可以运输600盒：5辆 $A$ 型冷链运输车与6辆 $B$ 型冷链运输车一次可以运输1350盒.

(1)、求每辆 $A$ 型车和每辆 $B$ 型车一次可以分别运输多少盒疫苗.

(2)、计划用两种冷链运输车共12辆运输这批疫苗， $A$ 型车一次需费用5000元， $B$ 型车一次需费用3000元.若运输物资不少于1500盒，且总费用小于54000元.请你列出所有运输方案，并指出哪种方案所需费用最少，最少费用是多少？

查看试题解析
30. 规定关于x的一元一次方程ax＝b的解为b-a，则称该方程是“郡园方程”，例如：3x＝4.5的解为4.5-3＝1.5，则该方程3x＝4.5就是“郡园方程”．

(1)、若关于x的一元一次方程2x＝m是“郡园方程”，求m的值；

(2)、若关于x的一元一次方程2x＝mn+m是“郡园方程”，它的解为m，求m，n的值；

(3)、若关于x的一元一次方程2x＝mn+m和-2x＝mn+n都是“郡园方程”，求代数式 $(m n + m)^{2} - 9 (m n + n)^{2} - \frac{3}{2} （ m - n)$ 的值．

查看试题解析
31. 有两个形状、大小完全相同的直角三角板ABC和CDE，其中∠ACB＝∠DCE＝90°．将两个直角三角板ABC和CDE如图①放置，点A，C，E在直线MN上．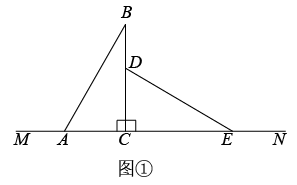

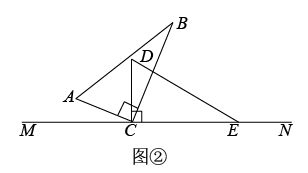(1)、三角板CDE位置不动，将三角板ABC绕点C顺时针旋转一周，
①在旋转过程中，若∠BCD＝35°，则∠ACE＝ ▲ °；
②在旋转过程中，∠BCD与∠ACE有怎样的数量关系？请依据图②说明理由．

(2)、在图①基础上，三角板ABC和CDE同时绕点C顺时针旋转，若三角板ABC的边AC从CM处开始绕点C顺时针旋转，转速为12°/秒，同时三角板CDE的边CE从CN处开始绕点C顺时针旋转，转速为2°/秒，当AC旋转一周再落到CM上时，两三角板都停止转动．如果设旋转时间为t秒，则在旋转过程中，当∠ACE＝2∠BCD时，t为多少秒？

查看试题解析