四川省巴中市2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-08-11 类型:期末考试
一、单选题
-
1. 第19届亚运会将于2022年9月在杭州举行,下列历届亚运会会徽是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 不等式x-1>0的解集在数轴上表示正确的是( )A、
2. 不等式x-1>0的解集在数轴上表示正确的是( )A、 B、
B、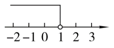 C、
C、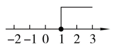 D、
D、 3. 如图,为估计池塘岸边A、B两点的距离,小明在池塘的一侧选取一点O,测得米,米,A、B间的距离不可能是( )
3. 如图,为估计池塘岸边A、B两点的距离,小明在池塘的一侧选取一点O,测得米,米,A、B间的距离不可能是( ) A、12米 B、10米 C、20米 D、8米4. 下列说法不正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 如图, , 若 , , 则的度数为( )
A、12米 B、10米 C、20米 D、8米4. 下列说法不正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 如图, , 若 , , 则的度数为( ) A、 B、 C、 D、6. 若一个三角形的三个内角度数的比为 ,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形7. 如图,把沿方向平移得到 , , 则的长是( )
A、 B、 C、 D、6. 若一个三角形的三个内角度数的比为 ,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形7. 如图,把沿方向平移得到 , , 则的长是( ) A、 B、 C、 D、8. 某工厂有26名工人,一个工人每天可加工800个螺栓或1000个螺帽,1个螺栓与2个螺帽配套,现要求工人每天加工的螺栓和螺帽完整配套且没有剩余.若设安排x个工人加工螺栓,y个工人加工螺帽,则列出正确的二元一次方程组为( )A、 B、 C、 D、9. 不等式组的所有整数解的和是( )A、2 B、3 C、5 D、610. 已知等腰三角形的两边长分别为x、y,且满足 , 则该等腰三角形的周长为( )A、22或26 B、17 C、17或22 D、2211. 下列说法正确的有( )个
A、 B、 C、 D、8. 某工厂有26名工人,一个工人每天可加工800个螺栓或1000个螺帽,1个螺栓与2个螺帽配套,现要求工人每天加工的螺栓和螺帽完整配套且没有剩余.若设安排x个工人加工螺栓,y个工人加工螺帽,则列出正确的二元一次方程组为( )A、 B、 C、 D、9. 不等式组的所有整数解的和是( )A、2 B、3 C、5 D、610. 已知等腰三角形的两边长分别为x、y,且满足 , 则该等腰三角形的周长为( )A、22或26 B、17 C、17或22 D、2211. 下列说法正确的有( )个①三角形的一个外角大于它的任何一个内角
②边形一共有条对角线
③三角形的中线在三角形内部
④两个图形关于某直线对称,对应点一定在该直线的两侧
⑤长方形既是中心对称图形又是轴对称图形.
A、1 B、2 C、3 D、412. 如图:已知 , BD、CD、BE分别平分的内角、外角、外角 , 其中点D、C、E在同一条直线上,以下结论:错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
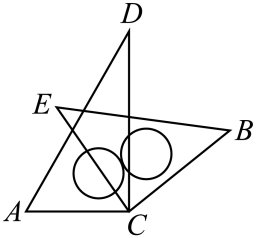
13. 一个正n边形的一个外角等于36°,则n= .14. 如图所示,王师傅做完门框为防止变形,在门上钉上AB、CD两条斜拉的木条,其中的数学原理是 .
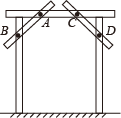 15. 若关于x的方程是一元一次方程,则 .16. 若关于x,y的方程组的解适合方程 , 则 .17. 用正三角形和正六边形作平面密铺,若每一个顶点周围有m个正三角形、n个正六边形,则m,n满足的关系式是.18. 如图,在长方形ABCD中, , , 点E是AD上一点, , 点P从点B出友,以1cm/s的速度从点B—C—D—E匀速运动,设点P运动的时间为ts,当的面积为6cm2时,则t= .
15. 若关于x的方程是一元一次方程,则 .16. 若关于x,y的方程组的解适合方程 , 则 .17. 用正三角形和正六边形作平面密铺,若每一个顶点周围有m个正三角形、n个正六边形,则m,n满足的关系式是.18. 如图,在长方形ABCD中, , , 点E是AD上一点, , 点P从点B出友,以1cm/s的速度从点B—C—D—E匀速运动,设点P运动的时间为ts,当的面积为6cm2时,则t= .
三、解答题
-
19.(1)、解方程:(2)、解方程组(3)、解不等式组 ,并把解集在数轴上表示出来.20. 甲、乙两人解关于x、y的方程组时,甲因看错a得到方程组的解为 , 乙将方程②中的b写成了它的相反数得到方程组的解为 .(1)、求a、b的值;(2)、求原方程组的解.21. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,的顶点都在格点上.
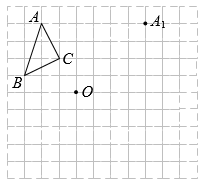 (1)、若与关于直线l成轴对称,点是点A的对称点,请在图中画出对称轴l和;(2)、画出关于点O的中心对称图形;(3)、在直线l上画一点P,使的周长最短.22. 对于任意有理数a、b、c、d,规定 , 已知 .(1)、用含x的代数式表示y;(2)、若的正整数解只有3个,求k的取值范围.23. 如图,AD、AF分别为的中线、高,点E为AD的中点.
(1)、若与关于直线l成轴对称,点是点A的对称点,请在图中画出对称轴l和;(2)、画出关于点O的中心对称图形;(3)、在直线l上画一点P,使的周长最短.22. 对于任意有理数a、b、c、d,规定 , 已知 .(1)、用含x的代数式表示y;(2)、若的正整数解只有3个,求k的取值范围.23. 如图,AD、AF分别为的中线、高,点E为AD的中点. (1)、若 , , 求的度数;(2)、若的面积为15, , 求AF的长.24. 张家口市某校为了普及推广冰雪活动进校园,准备购进速滑冰鞋和花滑冰鞋用于开展冰雪运动,若购进30双速滑冰鞋和20双花滑冰鞋共需8500元;若购进40双速滑冰鞋和10双花滑冰鞋共需8000元.(1)、求速滑冰鞋和花滑冰鞋每双购进价格分别为多少元?(2)、若该校购进两种冰鞋共50双,其中花滑冰鞋的数量不少于速滑冰鞋的数量,且用于购置两种冰鞋的总经费不超过8900元,则该校本次购买两种冰鞋共有哪几种方案?
(1)、若 , , 求的度数;(2)、若的面积为15, , 求AF的长.24. 张家口市某校为了普及推广冰雪活动进校园,准备购进速滑冰鞋和花滑冰鞋用于开展冰雪运动,若购进30双速滑冰鞋和20双花滑冰鞋共需8500元;若购进40双速滑冰鞋和10双花滑冰鞋共需8000元.(1)、求速滑冰鞋和花滑冰鞋每双购进价格分别为多少元?(2)、若该校购进两种冰鞋共50双,其中花滑冰鞋的数量不少于速滑冰鞋的数量,且用于购置两种冰鞋的总经费不超过8900元,则该校本次购买两种冰鞋共有哪几种方案?