陕西省榆林市神木市2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-11 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，在下列四个图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在人类的大脑中，有一种神经元的半径约为0.000027米，将数据0.000027用科学记数法表示为（）

A、 $2.7 \times 1 0^{- 5}$ B、 $2.7 \times 1 0^{- 6}$ C、 $27 \times 1 0^{- 5}$ D、 $27 \times 1 0^{- 6}$

查看试题解析
3. 经过有交通信号灯的路口，遇到红灯．这个事件是（）

A、必然事件 B、不可能事件 C、随机事件 D、确定性事件

查看试题解析
4. 有一个长为10，宽为6的长方形，若将长方形的宽增加 $x (0 < x < 4)$ ，长不变，所得新长方形的面积y与x之间的关系式为（）

A、 $y = 60 - x$ B、 $y = 10 x$ C、 $y = 60 + x$ D、 $y = 10 x + 60$

查看试题解析
5. 下列运算正确的是（）

A、 $x^{4} \cdot x^{2} = x^{6}$ B、 ${(x^{4})}^{2} = x^{6}$ C、 $x^{6} \div x^{2} = x^{3}$ D、 ${(- x y^{2})}^{3} = - x y^{6}$

查看试题解析
6. 小球在如图所示的地板上自由地滚动，随机地停留在某块方砖上，最终停在白色区域上的概率是（）

A、 $\frac{5}{13}$ B、 $\frac{8}{13}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
7. 如图，在四边形ABCD中，AB＝CD，连接BD，且 $B D = A B$ ．若 $∠ A B C = 13 0^{∘}$ ， $∠ C = 3 0^{∘}$ ，则∠A的度数为（）

A、 $2 0^{∘}$ B、 $2 5^{∘}$ C、 $3 0^{∘}$ D、 $4 0^{∘}$

查看试题解析
8. 如图，点D是△ABC内一点， $A D = C D$ ， $∠ A D B = ∠ C D B$ ，则以下结论① $∠ D A C = ∠ D C A$ ；② $A B = A C$ ；③BD平分∠ABC；④BD与AC的位置关系是互相垂直，其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

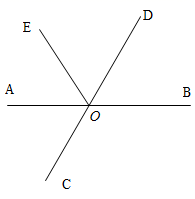
9. 比较大小： ${(\frac{1}{3})}^{- 1}$ ${(- 3)}^{0}$ （填“＞”“＜”或“＝”）

查看试题解析
10. 若长度分别为3，5，a的三条线段能组成一个三角形，则整数a的最大值为．

查看试题解析
11. 如图，直线AB，CD相交于点O，AO平分 $∠ C O E$ ，且 $∠ E O D = 50 °$ ，则 $∠ D O B$ 的度数是.

查看试题解析
12. 已知华氏温度F（℉）与摄氏温度（℃）之间的关系满足下表：
摄氏（单位℃）
…
－10
0
10
20
30
…
华氏（单位℉）
…
14
32
50
68
86
…
若火星上某处的温度大约是－50℃，则此温度换算成华氏温度约为℉．

查看试题解析
13. 如图，在 $△$ ABC中，BD平分∠ABC，过BC的中点E作BC的垂线交BD于点F，连接CF．若∠A＝50°，∠ACF=40°，则∠CFD的度数为.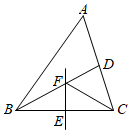

查看试题解析

三、解答题

14. 化简： $[(2 a + b) (2 a - b) - 4 {(a - b)}^{2} - b^{2}] \div (- 2 b)$ ．

查看试题解析
15. 如图，在方格纸上以虚线l为对称轴画出这个图形的另一半．

查看试题解析
16. 尺规作图，已知∠ $α$ ，线段a，b，求作△ABC，使得 $∠ B = ∠ α$ ， $A B = 2 a$ ， $B C = b$ ．（不写作法，保留作图痕迹）

查看试题解析
17. 如图，在四边形ABCD中， $A B ∥ C D$ ， $∠ B = ∠ D$ ，点E在AD上，点F在BC的延长线上，连接EF，试说明 $∠ D E F = ∠ F$ ．

查看试题解析
18. 如图，已知 $Δ A B C ≅ Δ D E C$ ，点E在AB边上，若 $∠ B = 7 0^{∘}$ ，求∠BCE的度数．

查看试题解析
19. 如图所示，已知△ABC的周长为21 cm，AB＝6 cm，BC边上中线AD＝5 cm，△ABD的周长为15 cm，求AC的长．

查看试题解析
20. 如图，BD是△ABC中∠ABC的平分线， $D E ⊥ A B$ 于点E ， $D F ⊥ B C$ 于点F，若DE＝3，AB＝7，BC＝9，求△ABC的面积．

查看试题解析
21. 某次大型活动，组委会启用无人机航拍活动过程，在操控无人机时应根据现场状况调节高度，无人机的飞行高度h（米）与操控无人机的时间t（分钟）之间的关系如图中的实线所示．
根据图象回答下列问题：

(1)、在上升或下降的过程中，无人机最高上升到米，在50米高处航拍的时间是分钟；

(2)、无人机返回地面的速度是多少？

查看试题解析
22. 如图，从一个长方形铁皮中剪去一个小正方形，长方形的长为（2a＋b）米，宽为（a＋b）米，正方形的边长为a米．

(1)、求剩余铁皮的面积；

(2)、当a＝3，b＝2时，求剩余铁皮的面积．

查看试题解析
23. 小明想知道一堵墙上点A到地面的高度AO，AO⊥OD，但又没有直接测量的工具，于是设计了下面的方案，请你先补全方案，再说明理由．

第一步：找一根长度大于OA的直杆，使直杆靠在墙上，且顶端与点A重合，记下直杆与地面的夹角∠ABO；

第二步：使直杆顶端竖直缓慢下滑，直到 $∠ O C D = ∠ A B O$ ，标记此时直杆的底端点D；

第三步：测量的长度，即为点A到地面的高度AO．

请说明小明这样测量的理由．

查看试题解析
24. 小明和小亮两位同学做掷骰子（质地均匀的正方体）游戏，他们共做了100次试验，结果如下：
朝上的点数
1
2
3
4
5
6
出现的次数
16
14
25
20
12
13

(1)、计算“1点朝上”的频率和“6点朝上”的频率；

(2)、小亮说：“若投掷1000次，则出现4点朝上的次数正好是200次”．小亮的说法正确吗？为什么？

(3)、小明将这枚骰子任意投掷一次，求朝上的点数大于或等于4的概率．

查看试题解析
25. 如图，在四边形ABCD中，AB∥CD，连接BD，点E在BD上，连接CE，若∠1＝∠2，AB＝ED.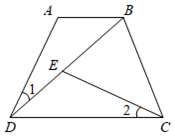

(1)、求证：BD＝CD.

(2)、若∠A＝120°，∠BDC＝2∠1，求∠DBC的度数.

查看试题解析
26. 如图，AE与BD相交于点C，AC＝EC，BC＝DC．

(1)、如图1，试说明： $A B ∥ D E$ ；

(2)、如图2，过点C作PQ交AB于P，交DE于Q，试说明 $C P = C Q$ ；

(3)、如图3，若AB＝8cm，点P从点A出发，沿A→B→A方向以3cm/s的速度运动，点Q从点D出发，沿D→E方向以1cm/s的速度运动，P、Q两点同时出发，当点P回到点A时，P、Q两点同时停止运动，设点P的运动时间为t（s），连接PQ，当线段PQ经过点C时，求出t的值．

查看试题解析

摄氏（单位℃）	…	－10	0	10	20	30	…
华氏（单位℉）	…	14	32	50	68	86	…

朝上的点数	1	2	3	4	5	6
出现的次数	16	14	25	20	12	13