（鲁教版）2022-2023学年度第一学期九年级数学第二章直角三角形的边角关系单元测试

试卷更新日期：2022-08-11 类型：单元试卷

进入出卷网下载

一、单选题

1. 在△ABC中，∠C＝90°，AB＝2，AC＝1，则cosB的值是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、2

查看试题解析
2. 在Rt△ABC中，∠C＝90°，若tan A＝ $\frac{3}{4}$ ，则sin A等于（）．

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{5}{3}$ D、 $\frac{3}{5}$

查看试题解析
3. 如图， $△ A B C$ 的三个顶点在边长为1的正方形网格的格点上，则 $tan (α + β)$ （） $t a n α + t a n β$ .

A、 $>$ B、 $<$ C、 $=$ D、 $\geq$

查看试题解析
4.
若计算器的四个键的序号如图所示，在角的度量单位为“度的状态下”用计算器求sin47°，正确的按键顺序是（　　）

A、（1）（2）（3）（4） B、（2）（4）（1）（3） C、（1）（4）（2）（3） D、（2）（1）（4）（3）

查看试题解析
5. 在Rt $△ A B C$ 中， $∠ C = 90^{°} ， \sin A = \frac{J}{5} ， A B = 5 cm$ ，则AC的长度是（）

A、3cm B、4cm C、5cm D、6cm

查看试题解析
6. 构造几何图形解决代数问题是“数形结合思想”的重要应用，小康在计算 $\tan 22.5 °$ 时，构造出如图所示的图形：在Rt $△$ ACD中， $∠ C = 90 °$ ， $∠ A B C = 45 °$ ，延长 $C B$ 到 $D$ ， $B D = A B$ ，连接 $A D$ ，得 $∠ D = 22.5 °$ ．根据此图可求得 $\tan 22.5 °$ 的结果（）

A、 $2 - \sqrt{3}$ B、 $\sqrt{2} + 1$ C、 $\sqrt{2} - 1$ D、 $2 - \sqrt{2}$

查看试题解析
7. 为了解决楼房之间的采光问题，我市有关部门规定：两幢楼房之间的最小距离要使中午12时不能遮光.如图，旧楼的一楼窗台高1米，现计划在旧楼右侧50米处再建一幢新楼.若我市冬天中午12时太阳照射的光线与水平线的夹角最小为α度，则新楼最高可建（ )

A、 $50 \tan α$ 米 B、 $\frac{50}{\tan α}$ 米 C、 $(50 \tan α + 1)$ 米 D、 $(\frac{50}{\tan α} + 1)$ 米

查看试题解析
8. 如图，推动个小球沿倾斜角为 $α$ 的斜坡向上行驶，若 $\sin α = \frac{5}{13}$ ，小球移动的水平距离 $A C = 12$ 米，那么小球上升的高度 $B C$ 是（）

A、5米 B、6米 C、6.5米 D、7米

查看试题解析
9. 在离旗杆20米处的地方，用测角仪测得旗杆项的仰角为 $α$ ，如测角仪的高为1.5米，那么旗杆的高为（）米

A、 $20 c o t α$ B、 $20 t a n α$ C、 $1.5 + 20 t a n α$ D、 $1.5 + 20 c o t α$

查看试题解析
10. 如图，一艘轮船在小岛A的西北方向距小岛 $40 \sqrt{2}$ 海里的C处，沿正东方向航行一段时间后到达小岛A的北偏东 $60 °$ 的B处，则该船行驶的路程为（）

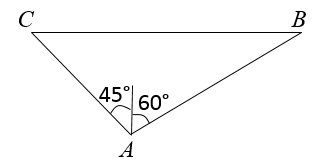A、80海里 B、120海里 C、 $(40 + 40 \sqrt{2})$ 海里 D、 $(40 + 40 \sqrt{3})$ 海里

查看试题解析

二、填空题

11. 如图，在每个小正方形的边长为1的网格中， $△ A B C$ 的顶点A、B、C均落在格点上，则 $\cos ∠ A B C =$ .

查看试题解析
12. 计算：（﹣2016）⁰＋|1﹣ $\sqrt{3}$ |﹣2sin60°＝．

查看试题解析
13. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，点D、点E分别在AB、AC上，连接CD、ED， $E D = C D$ ， $t a n ∠ A D E = \frac{1}{3}$ ， $B D = \sqrt{2}$ ，则 $A B =$ ．

查看试题解析
14. 如图，在A点有一个热气球，由于受西风的影响，以20米/分的速度沿与地面成 $75 °$ 角的方向飞行，10分钟后到达C处，此时热气球上的人测得地面上的B点俯角为 $30 °$ ，则A、B两点间的距离为米．

查看试题解析
15. 如图，码头A在码头B的正东方向，它们之间的距离为10海里．一货船由码头A出发，沿北偏东45°方向航行到达小岛C处，此时测得码头B在南偏西60°方向，那么码头A与小岛C的距离是海里（结果保留根号）．

查看试题解析

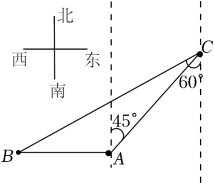
三、解答题

16. 如图，在 $Rt △ ABC$ 中， $∠ ACB = 90 ° ， CD ⊥ AB$ 于点D.若 $AD = 4 ， BD = 2$ ，求 $tanA$ 的值.

查看试题解析
17. 先化简，再求值： $(1 - \frac{1}{x + 2}) \div \frac{x^{2} - 1}{x + 2}$ ，其中 $x = 2 \sin 45 ° + \tan 45 °$ ．

查看试题解析
18. 如图，某地修建高速公路，要从A地向B地修一座隧道（A、B在同一水平面上），为了测量A、B两地之间的距离，某工程师乘坐热气球从B地出发，垂直上升100米到达C处，在C处观察A地的俯角为39°，求A、B两地之间的距离．（结果精确到1米）（参考数据：sin39°=0.63，cos39°=0.78，tan39°=0.81）

查看试题解析
19. 如图，已知Rt△ABC中，斜边BC上的高AD=4，cosB= 求AC边的长度

查看试题解析
20. 如图，在△ABC中，∠B＝45°，AB＝ $\sqrt{2}$ ，∠A＝105°，求△ABC的面积．

查看试题解析
21. 如图1是一间安装有壁挂式空调的卧室的一部分，如图2是该空调挂机的侧面示意图．已知空调挂机底部BC垂直于墙面CD，且当导风板所在的直线AE与竖直直线AB的夹角α为42°时，空调风刚好吹到床的外边沿E处， $C D ⊥ E D$ 于点D， $A B ⊥ E D$ 于点F．若 $A B = 0.02 m$ ， $B C = 0.2 m$ ，床铺 $E D = 2.4 m$ ，求空调机的底部位置距离床的高度CD．（结果精确到0.1m，参考数据： $s i n 42 ° \approx 0.67$ ， $c o s 42 ° \approx 0.74$ ， $t a n 42 ° \approx 0.90$ ）

查看试题解析
22. 钓鱼岛是我国固有领土，2021年4月26日，中华人民共和国自然资源部在其官网上公布《钓鱼岛及其附属岛屿地形地貌调查报告》，报告公布了钓鱼岛及其附属岛屿的高分辨率海岛地形数据．如图，点A是岛上最西端“西钓鱼”，点B是岛上最东端“东钓角”， $A B$ 长约3641米，点D是岛上的有小黄鱼岛，且 $A ， B ， D$ 三点共线．某日中国海监一艘执法船巡航到点C处时，恰好看到正北方的小黄鱼岛D，并测得 $∠ A C D = 70 °$ ， $∠ B C D = 45 °$ ．根据以上数据，请求出此时执法船距离小黄鱼岛D的距离 $C D$ （参考数据： $t a n 70 ° \approx 2.75$ ， $s i n 70 ° \approx 0.94$ ， $c o s 70 ° \approx 0.34$ ，结果精确到1米）．

查看试题解析
23. 如图，在鉴江的右岸边有一高楼AB，左岸边有一坡度i＝1：2的山坡CF，点C与点B在同一水平面上，CF与AB在同一平面内．某数学兴趣小组为了测量楼AB的高度，在坡底C处测得楼顶A的仰角为45°，然后沿坡面CF上行了20 $\sqrt{5}$ 米到达点D处，此时在D处测得楼顶A的仰角为30°，求楼AB的高度．

查看试题解析
24. 如图，小杰在湖边高出水面 $M N$ 约 $10 m$ 的平台A处发现一架无人机停留在湖面上空的点P处，该无人机在湖中的倒影为点 $P'$ ，小杰在A处测得点P的仰角为 $45 °$ ，点 $P'$ 的俯角为60 $°$ ，求该无人机离开湖面的高度（结果保留根号）．

查看试题解析

（鲁教版）2022-2023学年度第一学期九年级数学第二章 直角三角形的边角关系 单元测试

一、单选题

二、填空题

三、解答题

（鲁教版）2022-2023学年度第一学期九年级数学第二章直角三角形的边角关系单元测试