(鲁教版)2022-2023学年度第一学期九年级数学2.6 利用三角函数测高 同步测试
试卷更新日期:2022-08-11 类型:同步测试
一、单选题
-
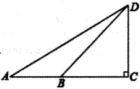
1. 如图,小明在学校操场A处测得旗杆的仰角为30°,沿AC方向行进10米至B处,测得仰角为45°,则旗杆的高度DC是( )
 A、米 B、米 C、10米 D、米2. 如图,小强从热气球上的A点测量一栋高楼顶部的仰角 , 测量这栋高楼底部的俯角 , 热气球与高楼的水平距离为米,则这栋高楼的高BC为( )米.
A、米 B、米 C、10米 D、米2. 如图,小强从热气球上的A点测量一栋高楼顶部的仰角 , 测量这栋高楼底部的俯角 , 热气球与高楼的水平距离为米,则这栋高楼的高BC为( )米. A、45 B、60 C、75 D、903. 某人沿着坡度为1∶的山坡前进了1000 m,则这个人所在的位置升高了( )A、1000 m B、500 m C、500m D、m4. 某人沿着倾斜角为 ,坡度为 的斜坡向上前进了 ,那么他的高度上升了( )A、 B、 C、 D、5. 一小球从斜坡的顶端沿斜坡向下滚落到斜坡底端,行了100米,下落的铅直高度为50米,则该斜坡的坡度为( )A、30° B、 C、 D、6. 如图,为测量一幢大楼的高度,在地面上与楼底点O相距30米的点A处,测得楼顶B点的仰角 , 则这幢大楼的高度为( )
A、45 B、60 C、75 D、903. 某人沿着坡度为1∶的山坡前进了1000 m,则这个人所在的位置升高了( )A、1000 m B、500 m C、500m D、m4. 某人沿着倾斜角为 ,坡度为 的斜坡向上前进了 ,那么他的高度上升了( )A、 B、 C、 D、5. 一小球从斜坡的顶端沿斜坡向下滚落到斜坡底端,行了100米,下落的铅直高度为50米,则该斜坡的坡度为( )A、30° B、 C、 D、6. 如图,为测量一幢大楼的高度,在地面上与楼底点O相距30米的点A处,测得楼顶B点的仰角 , 则这幢大楼的高度为( ) A、米 B、米 C、米 D、米7. 如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,则树高DE的长度为( )
A、米 B、米 C、米 D、米7. 如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,则树高DE的长度为( ) A、3 B、6 C、3 D、68. 如图要测量小河两岸相对的两点P,A的距离,点P位于点A正北方向,点C位于点A的北偏西46°,若测得PC=50米,则小河宽PA为( )
A、3 B、6 C、3 D、68. 如图要测量小河两岸相对的两点P,A的距离,点P位于点A正北方向,点C位于点A的北偏西46°,若测得PC=50米,则小河宽PA为( )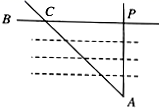 A、50sin44°米 B、50cos44° C、50tan44°米 D、50tan46°米9. 无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为的处测得试验田右侧出界处俯角为 , 无人机垂直下降至处,又测得试验田左侧边界处俯角为 , 则 , 之间的距离为(参考数据: , , , , 结果保留整数)( )
A、50sin44°米 B、50cos44° C、50tan44°米 D、50tan46°米9. 无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为的处测得试验田右侧出界处俯角为 , 无人机垂直下降至处,又测得试验田左侧边界处俯角为 , 则 , 之间的距离为(参考数据: , , , , 结果保留整数)( )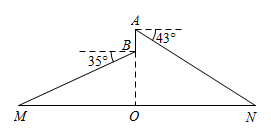 A、 B、 C、 D、10. 如图,某栋教学楼AB顶部竖有一块宣传牌BC,某同学从建筑物底端A点出发,沿水平方向向右走12米到达D点,在D处测得宣传牌底部B点的仰角是54°,再经过一段坡比为1:2.4,坡长为6.5米的斜坡DE到达E点(A、B、C、D、E均在同一平面内),在E处测得宣传牌的顶部C点的仰角是45°,则宣传牌BC的高度为( )(参考数据:sin54°≈0.80,cos54°≈0.59,tan54°≈1.38,结果精确到0.1米)
A、 B、 C、 D、10. 如图,某栋教学楼AB顶部竖有一块宣传牌BC,某同学从建筑物底端A点出发,沿水平方向向右走12米到达D点,在D处测得宣传牌底部B点的仰角是54°,再经过一段坡比为1:2.4,坡长为6.5米的斜坡DE到达E点(A、B、C、D、E均在同一平面内),在E处测得宣传牌的顶部C点的仰角是45°,则宣传牌BC的高度为( )(参考数据:sin54°≈0.80,cos54°≈0.59,tan54°≈1.38,结果精确到0.1米) A、1.4米 B、3.9米 C、4.0米 D、16.6米
A、1.4米 B、3.9米 C、4.0米 D、16.6米二、填空题
-
11. 某防洪大堤的横断面是如图所示的梯形ABCD,坝高 米,背水坡AB的坡度 ,则斜坡AB的长为米.
 12. 如图,一段铁路路基的横断面为等腰梯形,路基的上底宽AD为3米,路基高为1米,斜坡AB的坡度 , 那么路基的下底宽BC是米.
12. 如图,一段铁路路基的横断面为等腰梯形,路基的上底宽AD为3米,路基高为1米,斜坡AB的坡度 , 那么路基的下底宽BC是米. 13. 如果在A点处观察B点的仰角为 , 那么在B点处观察A点的俯角为(用含的式子表示)14. 如图,海中有一个小岛A,一艘轮船由西向东航行,在点处测得小岛A在它的北偏东方向上,航行12海里到达点处,测得小岛A在它的北偏东方向上,那么小岛A到航线的距离等于海里.
13. 如果在A点处观察B点的仰角为 , 那么在B点处观察A点的俯角为(用含的式子表示)14. 如图,海中有一个小岛A,一艘轮船由西向东航行,在点处测得小岛A在它的北偏东方向上,航行12海里到达点处,测得小岛A在它的北偏东方向上,那么小岛A到航线的距离等于海里.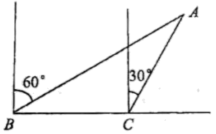 15. 如图,在点B处测得塔顶A的仰角为30°,点B到塔底C的水平距离BC是30m,那么塔AC的高度为m(结果保留根号).
15. 如图,在点B处测得塔顶A的仰角为30°,点B到塔底C的水平距离BC是30m,那么塔AC的高度为m(结果保留根号).
三、解答题
-
16. 如图,楼顶上有一个5G信号塔AB,从与楼BC相距60m的D处观测5G信号塔顶部A的仰角为37°,观测5G信号塔底部B的仰角为30°,求5G信号塔AB的高度.(结果保留小数点后一位,参考数据: , , , , ).
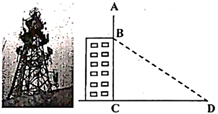 17. 青岛电视塔座落于样林公园内的太平山上,为测得电视塔的高度,如图所示,某同学在某栋楼的底部点D处看向电视塔底端的点B处,测得仰角是45°,在楼顶点E处,看向电视塔顶端C处,测得仰角是64°,已知楼高DE的高度为112米,AD⊥AC,DE∥AC,太平山的高度AB约为120米,求青岛电视塔BC的高度.(tan64°≈2)
17. 青岛电视塔座落于样林公园内的太平山上,为测得电视塔的高度,如图所示,某同学在某栋楼的底部点D处看向电视塔底端的点B处,测得仰角是45°,在楼顶点E处,看向电视塔顶端C处,测得仰角是64°,已知楼高DE的高度为112米,AD⊥AC,DE∥AC,太平山的高度AB约为120米,求青岛电视塔BC的高度.(tan64°≈2) 18. 我国首艘国产航母“山东”号是保障国土安全,维护祖国统一的又一利器.如图,一架歼15舰载机在航母正后方A点准备降落,此时在A测得航母舰首B的俯角为11.3°,舰尾C的俯角为14°,如果航空母舰长为315米且B比C高出10米,求舰载机相对舰尾C的高度(参考数据:sinl1.3°=0. 22, sin14°=0. 24,tanl1.3°=0.2,tan14° =0.25)
18. 我国首艘国产航母“山东”号是保障国土安全,维护祖国统一的又一利器.如图,一架歼15舰载机在航母正后方A点准备降落,此时在A测得航母舰首B的俯角为11.3°,舰尾C的俯角为14°,如果航空母舰长为315米且B比C高出10米,求舰载机相对舰尾C的高度(参考数据:sinl1.3°=0. 22, sin14°=0. 24,tanl1.3°=0.2,tan14° =0.25) 19. (材料阅读)2020年5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰,将用中国科技“定义”世界新高度,其基本原理之一是三角高程测量法,在山顶上立一个标杆,找到2个以上测量点,分段测量山的高度,再进行累加.因为地球面并不是水平的,光线在空气中会发生折射,所以当两个测量点的水平距离大于300m时,还要考虑球气差,球气差计算公式为 (其中d为两点间的水平距离,R为地球的半径,R取6400000m),即:山的海拔高度=测量点测得山的高度+测量点的海拔高度+球气差.
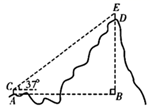
19. (材料阅读)2020年5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰,将用中国科技“定义”世界新高度,其基本原理之一是三角高程测量法,在山顶上立一个标杆,找到2个以上测量点,分段测量山的高度,再进行累加.因为地球面并不是水平的,光线在空气中会发生折射,所以当两个测量点的水平距离大于300m时,还要考虑球气差,球气差计算公式为 (其中d为两点间的水平距离,R为地球的半径,R取6400000m),即:山的海拔高度=测量点测得山的高度+测量点的海拔高度+球气差.(问题解决)某校科技小组的同学参加了一项野外测量某座山的海拔高度活动.如图,点A,B的水平距离d=800m,测量仪AC=1.5m,觇标DE=2m,点E,D,B在垂直于地面的一条直线上,在测量点A处用测量仪测得山顶标杆顶端E的仰角为37°,测量点A处的海拔高度为1800m.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).请你计算该山的海拔高度(要计算球气差,结果精确到0.01m).
 20. 《攀登者》于2019年9月30日在中国内地上映.展现出了中国登山队为了国家使命勇于攀登的精神.在2021年4月30日,一支登山队再一次成功地登上了珠峰之巅,站上了珠峰顶部.已知一个人登山时的动作可以简化成下图所示,他的大腿长AB=AC=45cm,上坡时大腿之间的夹角∠BAC=65°,某段山坡DF的坡度为i= , 大约走多少步才能将自己所处位置的海拔提高50米?
20. 《攀登者》于2019年9月30日在中国内地上映.展现出了中国登山队为了国家使命勇于攀登的精神.在2021年4月30日,一支登山队再一次成功地登上了珠峰之巅,站上了珠峰顶部.已知一个人登山时的动作可以简化成下图所示,他的大腿长AB=AC=45cm,上坡时大腿之间的夹角∠BAC=65°,某段山坡DF的坡度为i= , 大约走多少步才能将自己所处位置的海拔提高50米?(结果保留两位小数,sin65°≈ , tan65°≈ , cos65°≈)
 21. 下课时,数学老师给大家布置了一个任务:请大家在不攀爬到楼顶上的情况下,测出学校逸夫综合楼的高度.根据老师所给的任务,小慧站在与逸夫综合楼底部B在同一水平面且距离10米的C处,通过测角器观察逸夫综合楼的顶端A,此时测角器的示数为60°,小慧又请小敏帮量得此时测角器与地面的距离CD长为1米,如图.请你帮小慧算出学校逸夫综合楼的高度(结果精确到0.1米,参考数据: , , ).
21. 下课时,数学老师给大家布置了一个任务:请大家在不攀爬到楼顶上的情况下,测出学校逸夫综合楼的高度.根据老师所给的任务,小慧站在与逸夫综合楼底部B在同一水平面且距离10米的C处,通过测角器观察逸夫综合楼的顶端A,此时测角器的示数为60°,小慧又请小敏帮量得此时测角器与地面的距离CD长为1米,如图.请你帮小慧算出学校逸夫综合楼的高度(结果精确到0.1米,参考数据: , , ). 22. 从2020年3月开始,一群野生亚洲象从云南西双版纳傣族自治州走出丛林,一路北上,历经17个月迁徙逾500公里安全返回栖息地,引发国内外一波“观象热潮”.象群北移途经峨山县时,一头亚洲象曾脱离象群.如图,A,B,C分别表示峨山县、象群位置和独象位置.经测量,象群在峨山县西北方向约12公里处,独象位于象群的正东方向和峨山县北偏东30°方向的交汇处,请你计算此时独象距离象群多少公里?(结果保留根号)
22. 从2020年3月开始,一群野生亚洲象从云南西双版纳傣族自治州走出丛林,一路北上,历经17个月迁徙逾500公里安全返回栖息地,引发国内外一波“观象热潮”.象群北移途经峨山县时,一头亚洲象曾脱离象群.如图,A,B,C分别表示峨山县、象群位置和独象位置.经测量,象群在峨山县西北方向约12公里处,独象位于象群的正东方向和峨山县北偏东30°方向的交汇处,请你计算此时独象距离象群多少公里?(结果保留根号)