(鲁教版)2022-2023学年度第一学期九年级数学2.4 解直角三角形 同步测试
试卷更新日期:2022-08-11 类型:同步测试
一、单选题
-
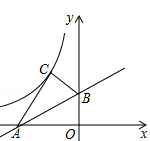
1. 如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线(k≠0)上,则k的值为( )
 A、4 B、﹣2 C、 D、2. 已知在RtABC中,∠C=90°,AB=c,AC=b,那么下列结论一定成立的是( )A、b=ctanA B、b=ccotA C、b=csinA D、b=ccosA3. 如图,已知太原南站某自动扶梯AB的倾斜角为31°,自动扶梯AB的长为15 m,则大厅两层之间的高度BC为( )
A、4 B、﹣2 C、 D、2. 已知在RtABC中,∠C=90°,AB=c,AC=b,那么下列结论一定成立的是( )A、b=ctanA B、b=ccotA C、b=csinA D、b=ccosA3. 如图,已知太原南站某自动扶梯AB的倾斜角为31°,自动扶梯AB的长为15 m,则大厅两层之间的高度BC为( ) A、 B、 C、 D、4. 已知在 中, , 那么 的长为( )A、 B、 C、 D、5. 已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( )
A、 B、 C、 D、4. 已知在 中, , 那么 的长为( )A、 B、 C、 D、5. 已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( ) A、2sin50° B、2sin40° C、2tan50° D、2tan40°6. 如图,某停车场入口的栏杆 , 从水平位置绕点O旋转到的位置,已知的长为5米.若栏杆的旋转角 , 则栏杆A端升高的高度为( )
A、2sin50° B、2sin40° C、2tan50° D、2tan40°6. 如图,某停车场入口的栏杆 , 从水平位置绕点O旋转到的位置,已知的长为5米.若栏杆的旋转角 , 则栏杆A端升高的高度为( ) A、米 B、米 C、米 D、米7. 将一副直角三角板如图放置,点在的延长线上, , , , , , 则的长为( )
A、米 B、米 C、米 D、米7. 将一副直角三角板如图放置,点在的延长线上, , , , , , 则的长为( ) A、 B、 C、 D、8. 如图,在边长为4的正方形ABCD中,点E是CD边上的一点,点F是点D关于直线AE对称的点,连接AF、BF,若tan∠ABF=2,则DE的长是( )
A、 B、 C、 D、8. 如图,在边长为4的正方形ABCD中,点E是CD边上的一点,点F是点D关于直线AE对称的点,连接AF、BF,若tan∠ABF=2,则DE的长是( )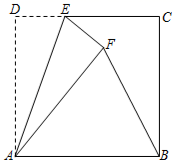 A、1 B、 C、 D、9. 如图,和都是等边三角形,且 , 当时,的面积为 , 则的边长为( )
A、1 B、 C、 D、9. 如图,和都是等边三角形,且 , 当时,的面积为 , 则的边长为( ) A、4 B、 C、 D、10. 如图,在边长为2的正方形 中,若将 绕点 逆时针旋转 ,使点 落在点 的位置,连接 ,过点 作 ,交 的延长线于点 ,则 的长为( )
A、4 B、 C、 D、10. 如图,在边长为2的正方形 中,若将 绕点 逆时针旋转 ,使点 落在点 的位置,连接 ,过点 作 ,交 的延长线于点 ,则 的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 定义:有一组对边相等而另一组对边不相等的凸四边形叫做“对等四边形”,如图,在中, , 点A在边BP上,点D在边CP上,如果 , , , 四边形ABCD为“对等四边形”,那么CD的长为 .
 12. 已知在 中, , 那么 .13. 在Rt△ABC中,∠C=90°,如果cosA= , AC=2,那么AB的长为 .14. 在中, , , 是BC上一点,把沿直线AE翻折后,点B落在点P处,如果 , 那么 .15. 如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为 .
12. 已知在 中, , 那么 .13. 在Rt△ABC中,∠C=90°,如果cosA= , AC=2,那么AB的长为 .14. 在中, , , 是BC上一点,把沿直线AE翻折后,点B落在点P处,如果 , 那么 .15. 如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为 .
三、解答题
-
16. 如图,在△ABC中,∠C=90°,∠A=45°,tan∠DBC= ,AB=4 ,求AD的长.
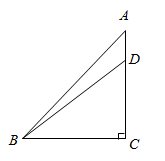 17. 如图,在Rt△ABC中,∠C=90°,BC=2,AC=2 .解这个直角三角形.
17. 如图,在Rt△ABC中,∠C=90°,BC=2,AC=2 .解这个直角三角形.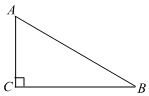 18. 如图,在 中, ,AD是BC边上的高,若 , ,求AC的长.
18. 如图,在 中, ,AD是BC边上的高,若 , ,求AC的长.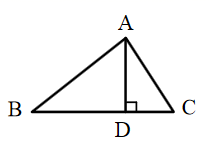 19. 已知点P是 上的一个动点,∠APB=118°,AB=10,点P到AB的最大距离约为多少?(结果保留整数,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60.)
19. 已知点P是 上的一个动点,∠APB=118°,AB=10,点P到AB的最大距离约为多少?(结果保留整数,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60.) 20. 如图,第二象限的角平分线 与反比例函数 的图象交于点A, 轴于点B, ,求 的值.
20. 如图,第二象限的角平分线 与反比例函数 的图象交于点A, 轴于点B, ,求 的值.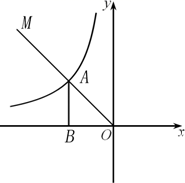 21. 构建几何图形解决代数问题是“数形结合”思想的重要策略.在计算 时,如图,在 中, ,延长 使 ,连接 ,得 ,所以 ,类比这种方法,计算 (画图并写出过程)
21. 构建几何图形解决代数问题是“数形结合”思想的重要策略.在计算 时,如图,在 中, ,延长 使 ,连接 ,得 ,所以 ,类比这种方法,计算 (画图并写出过程)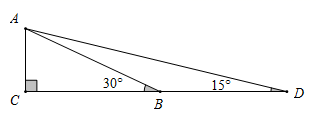 22. 如图,四边形ABCD中, , , , ,求AD的长.
22. 如图,四边形ABCD中, , , , ,求AD的长. 23. 如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端视线所及如图①所示.根据实际情况画出平面图形如图②, , , ,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是 的中点,路灯 高8米, 米, ,求甲、乙两人的观测点到地面的距离的差.
23. 如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端视线所及如图①所示.根据实际情况画出平面图形如图②, , , ,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是 的中点,路灯 高8米, 米, ,求甲、乙两人的观测点到地面的距离的差.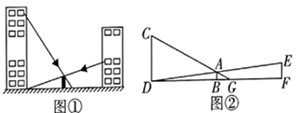 24. 去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向、B地的西偏北45°方向C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?( ≈1.732)
24. 去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向、B地的西偏北45°方向C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?( ≈1.732)