（鲁教版）2022-2023学年度第一学期九年级数学2.2 30°，45°，60°的三角函数值同步测试

试卷更新日期：2022-08-11 类型：同步测试

进入出卷网下载

一、单选题

1. 在正方形网格中， $△$ ABC的位置如图所示，点A、B、C均在格点上，则cosB的值为（）

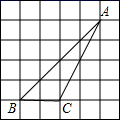A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{2}}{4}$

查看试题解析
2. 已知角α为 $△$ ABC的内角，且cosα= $\frac{2}{3}$ ，则α的取值范围是（）

A、0°<α<30° B、30°<α<45° C、45°<α<60° D、60°<α<90°

查看试题解析
3. 如图，已知：45°＜A＜90°，则下列各式成立的是（）

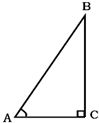A、sinA=cosA B、sinA＞cosA C、sinA＞tanA D、sinA＜cosA

查看试题解析
4. 点 $(- \sin 60 ° ， \cos 60 °)$ 关于y轴对称的点的坐标是（）

A、 $(\frac{\sqrt{3}}{2} ， \frac{1}{2})$ B、 $(- \frac{\sqrt{3}}{2} ， \frac{1}{2})$ C、 $(- \frac{\sqrt{3}}{2} ， - \frac{1}{2})$ D、 $(\frac{1}{2} ， \frac{3}{2})$

查看试题解析
5. 在RtΔABC中，若∠C=90°，cosA= $\frac{3}{5}$ ，则sinA的值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{5}{4}$

查看试题解析
6. 如图，梯子（长度不变）跟地面所成的锐角为A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是（）

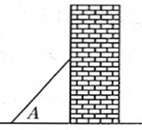A、sinA的值越大，梯子越陡 B、cosA的值越大，梯子越陡 C、tanA的值越小，梯子越陡 D、陡缓程度与∠A的三角函数值无关

查看试题解析
7. 已知 $α$ 为锐角，且 $s i n (90 ° - α) = \frac{1}{2}$ ，则 $α$ 的度数是（）

A、 $30^{\circ}$ B、 $45^{\circ}$ C、 $60^{\circ}$ D、 $75^{\circ}$

查看试题解析
8. 在 $△ A B C$ 中， $A$ ， $B$ 为锐角，且有 $\sin A = \cos B$ ，则这个三角形是（）

A、等腰三角形 B、直角三角形 C、钝角三角形 D、锐角三角形

查看试题解析
9. 如图，梯子（长度不变）跟地面所成的锐角为∠A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是（）

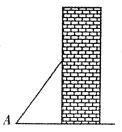A、sinA的值越大，梯子越陡 B、cosA的值越大，梯子越陡 C、tanA的值越小，梯子越陡 D、陡缓程度与∠A的三角函数值无关

查看试题解析
10. 在4×5网格中，A，B，C为如图所示的格点（小正方形的顶点），则下列等式正确的是（）

A、sinA= $\frac{\sqrt{3}}{2}$ B、cosA= $\frac{1}{2}$ C、tanA= $\frac{\sqrt{3}}{3}$ D、cosA= $\frac{\sqrt{2}}{2}$

查看试题解析

二、填空题

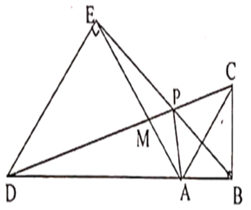
11. 计算 $2 s i n 6 0^{∘} t a n 6 0^{∘} - \sqrt{2} s i n 4 5^{∘} c o s 6 0^{∘}$ 的结果为．

查看试题解析
12. 若α是锐角且sinα= $\frac{\sqrt{3}}{2}$ ，则α的度数是．

查看试题解析
13. 在 $△ A B C$ 中， $∠ B = 75 °$ ， $t a n A = \sqrt{3}$ ，则 $∠ C$ 的度数是．

查看试题解析
14. 在△ABC中，∠A，∠C都是锐角，cosA＝ $\frac{1}{2}$ ， sinC＝ $\frac{\sqrt{3}}{2}$ ，则∠B＝．

查看试题解析
15. 如图，点A在线段BD上，在BD的同侧作等腰直角 $△ A B C$ 和等腰直角 $△ A D E$ ，CD与BE、AE分别交于点P，M.对于下列结论：① $△ B A E ∽ △ C A D$ ；② $M P . M D = M A \cdot M E$ ；③ $2 C B^{2} = C P \cdot C M$ ；④ $\sin ∠ C P B = \frac{\sqrt{3}}{2}$ ；其中正确的结论有.（写出所有正确结论的序号）

查看试题解析

三、解答题

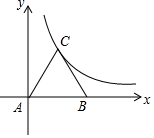
16. 先化简，再求值： $(\frac{x + 1}{x} - \frac{x}{x - 1}) \div \frac{1}{x}$ ，其中 $x = 2 s i n 45 ° + \sqrt{3} t a n 30 °$

查看试题解析
17. 如图，等边三角形ABC放置在平面直角坐标系中，已知A（0，0），B（4，0），反比例函数的图象经过点C.求点C的坐标及反比例函数的解析式.

查看试题解析
18. 已知∠A为锐角且sinA= $\frac{1}{2}$ ，则4sin²A－4sinAcosA＋cos²A的值是多少。

查看试题解析
19. 如图，点B是双曲线y＝ $\frac{k}{x}$ （k≠0）上的一点，点A在x轴上，且AB＝2，OB⊥AB ，若∠BAO＝60°，求k的值．

查看试题解析
20. 如图，“人字梯”放在水平地面上，梯子的两边相等(AB＝AC)，当梯子的一边AB与梯子两底端的连线BC的夹角α为60°时，BC的长为2米，若将α调整为65°时，求梯子顶端A上升的高度.(参考数据：sin65°≈0.91，cos65°＝0.42，tan65°≈2.41， $\sqrt{3}$ ＝1.73，结果精确到0.1m)

查看试题解析
21. 如图，在△ABC中，CD⊥AB，∠ACD＝45°，∠DCB＝60°，CD＝40，求AB．

查看试题解析
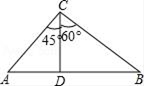22. 图1是安装在倾斜屋顶上的热水器，图2是安装热水器的侧面示意图．已知屋面AE的倾斜角∠EAD为22°，长为2米的真空管AB与水平线AD的夹角为37°，安装热水器的铁架竖直管CE的长度为0.5米．

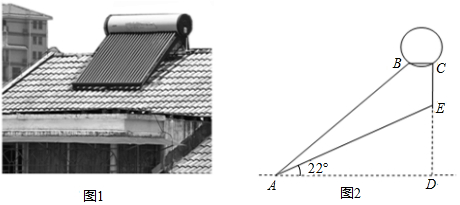(1)、真空管上端B到水平线AD的距离．

(2)、求安装热水器的铁架水平横管BC的长度（结果精确到0.1米）
（参考数据：sin37°≈ $\frac{3}{5}$ ，cos37°≈ $\frac{4}{5}$ ，tan37°≈ $\frac{3}{4}$ ，sin22°≈ $\frac{3}{8}$ ，cos22°≈ $\frac{15}{16}$ ，tan22°≈ $\frac{2}{5}$ ）

查看试题解析
23. 如图，在Rt△ABC中，∠C=90°，M是直角边AC上一点，MN⊥AB于点N，AN=3，AM=4，求cosB的值．

查看试题解析
24. 规定：sin（﹣x）=﹣sinx，cos（﹣x）=cosx，sin（x+y）=sinx•cosy+cosx•siny．据此

(1)、判断下列等式成立的是（填序号）．
①cos（﹣60°）=﹣ $\frac{1}{2}$ ；②sin2x=2sinx•cosx；③sin（x﹣y）=sinx•cosy﹣cosx•siny．

(2)、利用上面的规定求①sin75°，②sin15°．

查看试题解析

（鲁教版）2022-2023学年度第一学期九年级数学2.2 30°，45°，60°的三角函数值 同步测试

一、单选题

二、填空题

三、解答题

（鲁教版）2022-2023学年度第一学期九年级数学2.2 30°，45°，60°的三角函数值同步测试