（鲁教版）2022-2023学年度第一学期九年级数学第一章反比例函数单元测试

试卷更新日期：2022-08-11 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列函数中，y可以看作是x的反比例函数的是（）

A、 $y = \frac{2}{x^{2}}$ B、 $y = \frac{2 - x}{x}$ C、 $y = - \frac{1}{x} + 1$ D、 $y = - 2 x^{- 1}$

查看试题解析
2. 若函数 $y = \frac{k}{x}$ 的图象经过点A(2，4)，则 $k$ 的值为（）

A、4 B、-2 C、8 D、-8

查看试题解析
3. 下列函数中，图象经过点（2，﹣2）的反比例函数关系式是（）

A、 $y = \frac{4}{x}$ B、 $y = - \frac{4}{x}$ C、 $y = - \frac{2}{x}$ D、 $y = \frac{2}{x}$

查看试题解析
4. 下列函数中，当 $x > 0$ 时，y随x的增大而增大的是（）

A、 $y = - 3 x$ B、 $y = - x + 3$ C、 $y = - \frac{5}{x}$ D、 $y = \frac{1}{2 x}$

查看试题解析
5. 若点 $(- 2 ， y_{1})$ ， $(- 1 ， y_{2})$ ， $(2 ， y_{3})$ 在双曲线 $y = \frac{k}{x} (k < 0)$ 上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
6. 反比例函数y＝ $\frac{k}{x}$ 是经过点(2，3)，那么这个反比例函数的图象应在（）

A、第一、二象限 B、第一、三象限 C、第二，三象限 D、第二、四象限

查看试题解析
7. 在平面直角坐标系中，点P是y轴正半轴上的任意一点，过点P作x轴的平行线，分别与反比例函数y $= - \frac{12}{x}$ 和y $= \frac{16}{x}$ 的图象交于点A和点B，若点C是x轴上任意一点，连接AC、BC，则△ABC的面积为（）

A、10 B、12 C、14 D、28

查看试题解析
8. 在一个可以改变容积的密闭容器内，装有一定质量m的某种气体，当改变容积V时，气体的密度ρ也随之改变ρ与V在一定范围内满足ρ= $\frac{m}{V}$ ，它的图象如图所示，则该气体的质量m为（）

A、1.4kg B、5kg C、6.4kg D、7kg

查看试题解析
9. 某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为 $18^{\circ} C$ 的条件下生长最快的新品种．如图是某天恒温系统从开启到关闭及关闭后，大棚内温度 $y (^{\circ} C)$ 随时间 $x$ （小时）变化的函数图象，其中 $B C$ 段是双曲线 $y = \frac{k}{x} (k \neq 0)$ 的一部分，则当 $x = 16$ 时，大棚内的温度约为（）

A、 $18^{\circ} C$ B、 ${15.5}^{\circ} C$ C、 ${13.5}^{\circ} C$ D、 $12^{\circ} C$

查看试题解析
10. 如果以 $12 m^{3} / h$ 的速度向水箱注水，5h可以注满.为了赶时间，现增加进水管，使进水速度达到 $Q (m^{3} / h)$ ，那么此时注满水箱所需要的时间 $t (h)$ 与 $Q (m^{3} / h)$ 之间的函数关系式为（）

A、 $t = \frac{60}{Q}$ B、 $t = 60 Q$ C、 $t = 12 - \frac{60}{Q}$ D、 $t = 12 + \frac{60}{Q}$

查看试题解析

二、填空题

11. 如图，在平面直角坐标系中，Rt△ABC的顶点A，C的坐标分别是(0，2)，(2，0)，∠ACB＝90°，AC＝2BC．若函数y $= \frac{k}{x}$ （k＞0，x＞0）的图象经过点B，则k的值为．

查看试题解析
12. 如在平面直角坐标系中，等腰直角△ABO如图放置，直角顶点A在反比例函数 $y = \frac{k}{x}$ 的图形上，其中AB＝AO，B（－2，0），则k＝．

查看试题解析
13. 如图，双曲线 $y = \frac{k}{x}$ 经过Rt $△ B O C$ 斜边上的中点A，与BC交于点D， $S_{△ B O D} = 21$ ，则 $k =$ .

查看试题解析
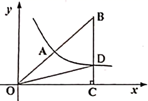14. 如图，点A₁、A₂、A₃…An在x轴正半轴上，点B₁、B₂、B₃…Bn在反比例函数 $y = \frac{k}{x}$ （k＞0，x＞0）图象上，OA₁＝A₁A₂＝A₂A₃＝…＝An_－₁An，记矩形OA₁B₁C₁面积为S₁、矩形A₁A₂B₂C₂面积为S₂、矩形A₂A₃B₃C₃面积为S₃……，则S₂₀₂₁＝（用含k的代数式表示）．

查看试题解析

15. 近视镜镜片焦距

y

（米）是镜片度数

x

（度）的某种函数，下表记录了一些数据：

$x$ （度）	…	$100$	$250$	$400$	$500$	…
$y$ （米）	…	$1.00$	$0.40$	$0.25$	$0.20$	…

利用表格中的数据关系计算：当镜片度数为 $200$ 度时，镜片焦距为米．

查看试题解析

三、解答题

16. 若A（3，2）与B（1，a）是反比例函数y＝ $\frac{k}{x}$ （k≠0）图象上的点，求a的值.

查看试题解析
17. 已知反比例函数 $y = \frac{m - 5}{x}$ 的图象过点P（－1，3），求m的值和该反比例函数的表达式.

查看试题解析
18. 设面积为 $20 c m^{2}$ 的平行四边形的一边长为 $a c m$ ，这条边上的高为 $h c m$ ．求 $h$ 关于 $a$ 的函数解析式(写出自变量 $a$ 的取值范围)并求当 $h = 5$ 时， $a$ 的值．

查看试题解析
19. 已知：如图所示，反比例函数 $y = \frac{k}{x}$ 的图象与正比例函数 $y = m x$ 的图象交于A、B，作AC⊥ $y$ 轴于C，连BC，则△ABC的面积为3，求反比例函数的解析式．

查看试题解析
20. 如图，已知双曲线 $y = \frac{k}{x}$ （x＞0）经过长方形OABC的边AB的中点F，交BC于点E，且四边形OEBF的面积为2，求k的值．

查看试题解析
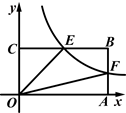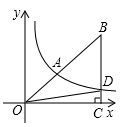21. 如图所示，双曲线 $y = \frac{k}{x} (k > 0)$ 经过 $R t △ B O C$ 斜边上的点A，且满足 $\frac{A O}{A B} = \frac{2}{3}$ ，与 $B C$ 交于点D， $S_{△ B O D} = 21$ ，求k的值.

查看试题解析
22. 如图，四边形OABC是矩形，ADEF是正方形，点A、D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B，E在反比例函数y＝ $\frac{k}{x}$ 的图象上，OA＝1，OC＝6，试求出正方形ADEF的边长.

查看试题解析
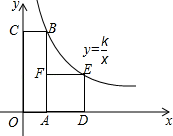23.
如图，已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上，顶点B的坐标是（6，4），反比例函数y= $\frac{k}{x}$ （x＞0）的图象经过矩形对角线的交点E，且与BC边交于点D．
（1）①求反比例函数的解析式与点D的坐标；
②直接写出△ODE的面积；
（2）若P是OA上的动点，求使得“PD+PE之和最小”时的直线PE的解析式．

查看试题解析
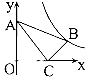
24.
如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，8），点P在边BC上以每秒1个单位长的速度由点C向点B运动，同时点Q在边AB上以每秒a个单位长的速度由点A向点B运动，运动时间为t秒（t＞0）．

（1）若反比例函数y= $\frac{m}{x}$ 图象经过P点、Q点，求a的值；

（2）若OQ垂直平分AP，求a的值；

（3）当Q点运动到AB中点时，是否存在a使△OPQ为直角三角形？若存在，求出a的值，若不存在请说明理由；

查看试题解析

（鲁教版）2022-2023学年度第一学期九年级数学第一章 反比例函数 单元测试

一、单选题

二、填空题

三、解答题

（鲁教版）2022-2023学年度第一学期九年级数学第一章反比例函数单元测试