(鲁教版)2022-2023学年度第一学期九年级数学1.2 反比例函数的图像和性质 同步测试
试卷更新日期:2022-08-11 类型:同步测试
一、单选题
-
1. 在反比例函数 的图象的每一条曲线上,y随x的增大而增大,则k的值可以是( )A、-1 B、0 C、1 D、22. 若点A(-1, ),B(1, ),C(2, )在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、3. 已知反比例函数 (k>0)的图象经过点A(-1,a)、B(-3,b),则a与b的关系正确的是( )A、a=b B、a= -b C、a<b D、a>b4. 如图,正方形ABCD的相邻两个顶点C、D分别在x轴、y轴上,且满足BD∥x轴,反比例函数y=(x<0)的图象经过正方形的中心E,若正方形的面积为8,则该反比例函数的解析式为( )
 A、y= B、y=- C、y= D、y=-5. 若 , 则反比例函数与一次函数在同一坐标系中的大致图象可能是( )A、
A、y= B、y=- C、y= D、y=-5. 若 , 则反比例函数与一次函数在同一坐标系中的大致图象可能是( )A、 B、
B、 C、
C、 D、
D、 6. 关于反比例函数的图象性质,下列说法不正确的是( )A、图象经过点 B、图象位于第一、三象限 C、当时,随的增大而增大 D、图象关于原点成中心对称7. 若反比例函数的图象上有两点A(−2,m),B(−1,n),则m,n的关系是( )A、 B、m<n C、m=n D、无法确定8. 已知y是x的反比例函数,如表给出了x与y的一些值,表中“▲”处的数为( )
6. 关于反比例函数的图象性质,下列说法不正确的是( )A、图象经过点 B、图象位于第一、三象限 C、当时,随的增大而增大 D、图象关于原点成中心对称7. 若反比例函数的图象上有两点A(−2,m),B(−1,n),则m,n的关系是( )A、 B、m<n C、m=n D、无法确定8. 已知y是x的反比例函数,如表给出了x与y的一些值,表中“▲”处的数为( )x
﹣2
2
3
y
3
﹣3
▲
A、2 B、﹣2 C、1 D、﹣19. 如图,AB⊥x轴,B为垂足,双曲线(x>0)与△AOB的两条边OA,AB分别相交于C,D两点,OC=CA,△ACD的面积为3,则k等于( )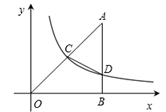 A、2 B、3 C、4 D、610. 如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
A、2 B、3 C、4 D、610. 如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )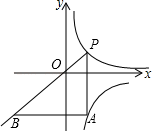 A、逐渐变大或变小 B、等于定值16 C、等于定值8 D、另有答案
A、逐渐变大或变小 B、等于定值16 C、等于定值8 D、另有答案二、填空题
-
11. 如图,已知 , 是反比例函数 图象上的两点,动点 在x轴正半轴上运动,当 达到最大时,点P的坐标是.
 12. 如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .
12. 如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .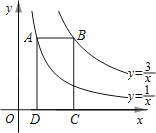 13. 若反比例函数 (k≠0)的图象经过点(-1,2),则k的值是.14. 若双曲线 在第二、四象限,则直线y=kx-2不经过第象限.15. 如图,点、都在反比例函数的图象上,点是直线上的一个动点,则的最小值是 .
13. 若反比例函数 (k≠0)的图象经过点(-1,2),则k的值是.14. 若双曲线 在第二、四象限,则直线y=kx-2不经过第象限.15. 如图,点、都在反比例函数的图象上,点是直线上的一个动点,则的最小值是 .
三、解答题
-
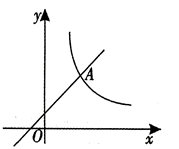
16. 如图,一次函数y=x+1的图像与反比例函数y的图像相交,其中一个交点的横坐标是2.求反比例函数的解析式.
 17. 如图,一次函数 的函数图象与反比例函数 的图象交于点A(2,3)和点B,与x轴相交于点C(8,0).求这两个函数的解析式;
17. 如图,一次函数 的函数图象与反比例函数 的图象交于点A(2,3)和点B,与x轴相交于点C(8,0).求这两个函数的解析式; 18. 如图,点A在反比例函数 的图象上,过点A作y轴的平行线交反比例函数 的图象于点B , 点C在y轴上,若 的面积为8,求k的值.
18. 如图,点A在反比例函数 的图象上,过点A作y轴的平行线交反比例函数 的图象于点B , 点C在y轴上,若 的面积为8,求k的值. 19. 已知函数 , ,当 时,函数 的最大值是 ,函数 的最小值是 ,求 和 的值.20. 如图,点A是反比例函数y=图象上的一点,过点A作AB⊥x轴于点B,连接OA,若△OAB的面积为2,求该反比例函数的解析式.
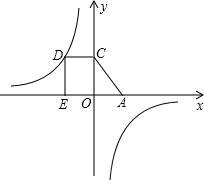
19. 已知函数 , ,当 时,函数 的最大值是 ,函数 的最小值是 ,求 和 的值.20. 如图,点A是反比例函数y=图象上的一点,过点A作AB⊥x轴于点B,连接OA,若△OAB的面积为2,求该反比例函数的解析式. 21. 如图,D为反比例函数 的图象上一点,过D作DE⊥x轴于点E , DC⊥y轴于点C , 一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
21. 如图,D为反比例函数 的图象上一点,过D作DE⊥x轴于点E , DC⊥y轴于点C , 一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.