山东省百校联考2021-2022学年高二下学期数学期末考试试卷
试卷更新日期:2022-08-09 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 设命题 , , 则为( )A、 , B、 , C、 , D、 ,3. 已知定义在R上的函数 , , , ,则a,b,c的大小关系为( )A、 B、 C、 D、4. 中国的技术世界领先,其数学原理之一便是著名的香农公式:.它表示:在受噪声干扰的信道中,最大信息传递速率(单位:)取决于信道宽度(单位:)、信道内信号的平均功率(单位:)、信道内部的高斯噪声功率(单位:)的大小,其中叫做信噪比,按照香农公式,若信道宽度变为原来2倍,而将信噪比从1000提升至4000,则大约增加了( )(附:)A、110% B、120% C、130% D、140%5. 若函数(且)在上为减函数,则函数的图象可以是( )A、
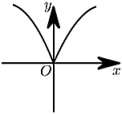 B、
B、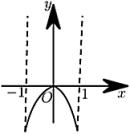 C、
C、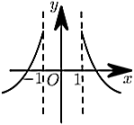 D、
D、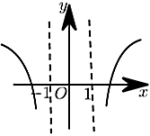 6. 满足函数 在 上单调递减的一个充分不必要条件是( )A、 B、 C、 D、7. 设函数f(x)的定义域为R , f(x+1)为奇函数,f(x+2)为偶函数,当 时, .若 ,则 ( )A、 B、 C、 D、8. 已知 , , 记 , 则( )A、M的最小值为 B、M的最小值为 C、M的最小值为 D、M的最小值为
6. 满足函数 在 上单调递减的一个充分不必要条件是( )A、 B、 C、 D、7. 设函数f(x)的定义域为R , f(x+1)为奇函数,f(x+2)为偶函数,当 时, .若 ,则 ( )A、 B、 C、 D、8. 已知 , , 记 , 则( )A、M的最小值为 B、M的最小值为 C、M的最小值为 D、M的最小值为二、多选题
-
9. 已知函数 ,则下列说法正确的是( )A、 为奇函数 B、 为减函数 C、 有且只有一个零点 D、 的值域为10. 下列说法不正确的是( )A、已知集合 , , 若 , 则实数m组成的集合为 B、不等式对一切实数恒成立的充要条件是 C、命题 , 成立的充要条件是 D、“”是“”的充分不必要条件11. 若函数(是自然对数的底数)在的定义域上单调递增,则称函数具有M性质.下列函数中具有M性质的是( )A、 B、 C、 D、12. 已知函数 , 结论正确的有( )A、是周期函数 B、的图象关于原点对称 C、的值域为 D、在区间上单调递增
三、填空题
-
13. 若函数的定义域为 , 则函数的定义域为.14. 已知函数则.15. 对于函数 , 若在定义域内存在实数满足 , 则称函数为“倒戈函数”.设( , 且)是定义在[﹣1,1]上的“倒戈函数”,则实数的取值范围是 .16. 已知函数与的图象上存在关于原点对称的对称点,(1)、求;(2)、则实数a的取值范围是.
四、解答题
-
17. 已知函数定义在上有恒成立,且当时,.(1)、求的值及函数的解析式;(2)、求函数的值域.18. 已知 ,函数 .(1)、当 时,解不等式 ;(2)、若函数 只有一个零点,求实数 的取值范围;19. 设函数 , 曲线在点处的切线方程为.(1)、求 , 的值;(2)、设函数.
①若在区间上单调递增,实数的取值范围;
②若在区间内存在单调递减的区间,求实数的取值范围.
20. 某公司研发甲、乙两种新产品,根据市场调查预测,甲产品的利润y(单位:万元)与投资 (单位:万元)满足: ( 为常数),且曲线 与直线 在(1,3)点相切;乙产品的利润与投资的算术平方根成正比,且其图像经过点(4,4).(1)、分别求甲、乙两种产品的利润与投资资金间的函数关系式;(2)、已知该公司已筹集到40万元资金,并将全部投入甲、乙两种产品的研发,每种产品投资均不少于10万元.问怎样分配这40万元投资,才能使该公司获得最大利润?其最大利润约为多少万元?(参考数据: )