陕西省榆林市高新区2021-2022学年七年级下学期期末考试数学试卷
试卷更新日期:2022-08-09 类型:期末考试
一、选择题(共8小题,每小题3分,计24分.)
-
1. “购买1张彩票,恰好中奖”这个事件是( )A、随机事件 B、确定事件 C、不可能事件 D、必然事件2. 在下面4个图形中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,直线 , 则( )
3. 如图,直线 , 则( ) A、 B、 C、 D、4. 已知三角形两边的长分别为1,5,第三边的长为整数,则第三边的长为( )A、4 B、5 C、6 D、75. 下列整式运算正确的是( )A、 B、 C、 D、6. 如图,曲线表示一只蝴蝶在飞行过程中离地面的高度h(m)随飞行时间t(s)的变化情况,则这只蝴蝶飞行的最高高度约为( )
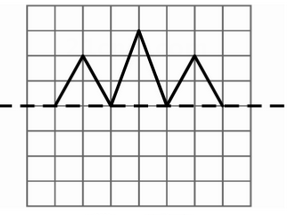
A、 B、 C、 D、4. 已知三角形两边的长分别为1,5,第三边的长为整数,则第三边的长为( )A、4 B、5 C、6 D、75. 下列整式运算正确的是( )A、 B、 C、 D、6. 如图,曲线表示一只蝴蝶在飞行过程中离地面的高度h(m)随飞行时间t(s)的变化情况,则这只蝴蝶飞行的最高高度约为( ) A、13m B、10mD.5m C、7m D、去学校劳动基地浇水,选中甲7. 老师从甲、乙、丙同学的概率是同学的概率是( )A、 B、 C、 D、8. 习题课上,张老师和同学们一起探究一个问题:“如图,在中,分别是上的点,与相交于点 , 添加下列哪个条件能判定是等腰三角形?"请你判断正确的条件应为( )
A、13m B、10mD.5m C、7m D、去学校劳动基地浇水,选中甲7. 老师从甲、乙、丙同学的概率是同学的概率是( )A、 B、 C、 D、8. 习题课上,张老师和同学们一起探究一个问题:“如图,在中,分别是上的点,与相交于点 , 添加下列哪个条件能判定是等腰三角形?"请你判断正确的条件应为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共5小题,每小题3分,计15分)
-
9. 比较大小:(选填“>”“=”或“<”)10. 若与是对顶角,与互余,且 , 则的度数为°.11. 王大斧要围成如图所示的长方形的菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为18米,设边的长为米,边的长为米,则与的关系式是。
 12. 一个小球在如图所示的地板上自由滚动,并随机停留在某块方砖上,每块方砖的大小、质地完全相同,那么该小球停留在白色区域的概率是。
12. 一个小球在如图所示的地板上自由滚动,并随机停留在某块方砖上,每块方砖的大小、质地完全相同,那么该小球停留在白色区域的概率是。 13. 如图,在中,.点在直线上,动点从点出发沿的路径向终点运动;动点从点出发沿路径向终点运动.点和点分别以每秒1cm和2cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,分别过点和作直线于直线于.当点运动时间为秒时,与全等.
13. 如图,在中,.点在直线上,动点从点出发沿的路径向终点运动;动点从点出发沿路径向终点运动.点和点分别以每秒1cm和2cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,分别过点和作直线于直线于.当点运动时间为秒时,与全等.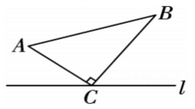
三、解答题(共13小题,计81分.解答应写出过程)
-
14. 化简:.15. 以图中的虚线为对称轴画出该图形的另一半.
 16. 如图,在中,点在上,平分 , 延长到点 , 使得 , 连接 , 若 , 求的度数.
16. 如图,在中,点在上,平分 , 延长到点 , 使得 , 连接 , 若 , 求的度数. 17. 如图,已知Rt和射线 , 请用尺规作图法,在上求作一点 , 使得.(保留作图痕迹,不写作法)
17. 如图,已知Rt和射线 , 请用尺规作图法,在上求作一点 , 使得.(保留作图痕迹,不写作法) 18. 如图,在Rt中,平分 , 交于点于点 , 连接 , 过点作 , 交于点.试说明:平分.
18. 如图,在Rt中,平分 , 交于点于点 , 连接 , 过点作 , 交于点.试说明:平分. 19. 在一个不透明的盒子里装有红、白两种颜色的球共10个,这些球除颜色外都相同.小颖将球搅匀,从盒子里随机摸出一个球记下颜色后,再把球放回盒子,不断重复上述过程.下表是多次摸球试验中的一组统计数据:
19. 在一个不透明的盒子里装有红、白两种颜色的球共10个,这些球除颜色外都相同.小颖将球搅匀,从盒子里随机摸出一个球记下颜色后,再把球放回盒子,不断重复上述过程.下表是多次摸球试验中的一组统计数据:摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
64
124
178
302
481
599
1803
摸到白球的频率
0.64
0.62
0.593
0.604
0.601
0.599
0.601
(1)、请估计:当很大时,摸到白球的频率将会接近;(精确到0.1)(2)、若从盒子里随机摸出一个球,求摸到白球的概率的估计值.(精确到0.1)20. 如图是一张简易木床的侧面图,现要钉上两根木条以确保其坚固耐用,木条已经钉上了 , 如果为了美观,要求木条与木条等长,那么应该怎样确定点的位置?并说明理由.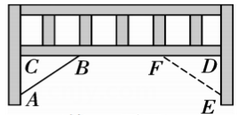 21. 如图,在一个边长为的大正方形纸片中,剪去一个长为、宽为的长方形和一个边长为的小正方形.
21. 如图,在一个边长为的大正方形纸片中,剪去一个长为、宽为的长方形和一个边长为的小正方形.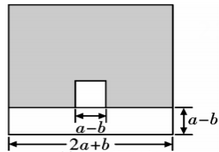 (1)、用含的式子表示阴影部分的面积;(结果化为最简)(2)、当时,求阴影部分的面积.22. 如图,已知点在上,平分平分.
(1)、用含的式子表示阴影部分的面积;(结果化为最简)(2)、当时,求阴影部分的面积.22. 如图,已知点在上,平分平分. (1)、试说明:;(2)、若 , 试判断与平行吗?为什么?23. 如图,某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:每购买500元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准的区域,顾客就可以分别获得500元、200元、100元、50元、10元的购物券一张(转盘等分成20份,如果指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止).
(1)、试说明:;(2)、若 , 试判断与平行吗?为什么?23. 如图,某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:每购买500元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准的区域,顾客就可以分别获得500元、200元、100元、50元、10元的购物券一张(转盘等分成20份,如果指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止). (1)、小华购物450元,他获得购物券的概率是多少?(2)、小丽购物600元,那么:
(1)、小华购物450元,他获得购物券的概率是多少?(2)、小丽购物600元,那么:①她获得50元购物券的概率是多少?
②她获得100元以上(包括100元)购物券的概率是多少?
24. 如图,点是边上一点, , 过点作 , 且 , 连接交于点 , 连接.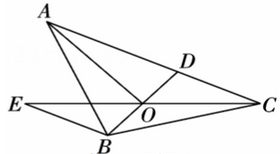 (1)、试说明:平分;(2)、若 , 求的度数.25. 一种豆子每千克的售价是2元,豆子的总售价(元)与售出豆子的质量(千克)之间的关系如下表:
(1)、试说明:平分;(2)、若 , 求的度数.25. 一种豆子每千克的售价是2元,豆子的总售价(元)与售出豆子的质量(千克)之间的关系如下表:售出豆子质量x(千克)
0
0.5
1
1.5
2
2.5
3
5
总售价y(元)
0
1
2
3
4
5
6
10
(1)、在这个表格中反映的是哪两个变量之间的关系?自变量是什么?因变量是什么?(2)、随着的逐渐增大,的变化趋势是怎样的?(3)、当豆子售出5千克时,总售价是多少元?(4)、预测一下,当豆子售出10千克时,总售价是多少元?26. 如图,在中, , 点为内一点,且恰好平分为延长线上一点,.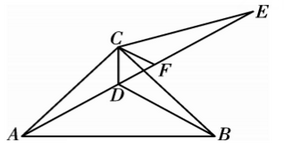 (1)、吗?为什么?(2)、若 , 求的度数;(3)、点在上,连接 , 若 , 试说明.
(1)、吗?为什么?(2)、若 , 求的度数;(3)、点在上,连接 , 若 , 试说明.