陕西省榆林市府谷县2021-2022学年八年级下学期期末质量抽样监测数学试卷
试卷更新日期:2022-08-09 类型:期末考试
一、选择题(共8小题,每小题3分,计24分.)
-
1. 围棋起源于中国,古代称之为“恋”,至今已有4000多年的历史.以下是在棋谱中截取的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 用反证法证明命题“已知在中, , 则”时,首先应该假设( )A、 B、 C、 D、且3. 下列各式中,能用平方差公式分解因式的是( )A、 B、 C、 D、4. 在 ▱ABCD中,若∠A+∠C=100°,则∠D的度数为( )A、 B、 C、 D、5. 已知关于的分式方程有增根,则的值为( )A、-3 B、1 C、2 D、36. 如图,点在内,且到三边的距离相等,连接 , 若 , 则的度数是( )
2. 用反证法证明命题“已知在中, , 则”时,首先应该假设( )A、 B、 C、 D、且3. 下列各式中,能用平方差公式分解因式的是( )A、 B、 C、 D、4. 在 ▱ABCD中,若∠A+∠C=100°,则∠D的度数为( )A、 B、 C、 D、5. 已知关于的分式方程有增根,则的值为( )A、-3 B、1 C、2 D、36. 如图,点在内,且到三边的距离相等,连接 , 若 , 则的度数是( ) A、 B、 C、 D、7. 某次知识竞赛一共有20道题,答对一题得5分,不答得0分,答错扣2分.小聪有1道题没答,竞赛成绩超过80分,则小聪至少答对的题数是( )A、15道 B、16道 C、17道 D、18道8. 如图,是等边三角形,点在的延长线上,点是的中点,连接并延长交于点 , 且 , 若 , 则的长为( )
A、 B、 C、 D、7. 某次知识竞赛一共有20道题,答对一题得5分,不答得0分,答错扣2分.小聪有1道题没答,竞赛成绩超过80分,则小聪至少答对的题数是( )A、15道 B、16道 C、17道 D、18道8. 如图,是等边三角形,点在的延长线上,点是的中点,连接并延长交于点 , 且 , 若 , 则的长为( ) A、3 B、4 C、6 D、8
A、3 B、4 C、6 D、8二、填空题(共5小题,每小题3分,计15分)
-
9. 若分式 有意义,则 的取值范围是.10. 多项式的各项公因式是.11. 已知一个多边形的每一个内角都是其相邻外角的5倍,则该多边形的边数为.12. 若关于x的不等式组有四个整数解,则m的取值范围是.13. 如图,在 ▱ ABCD中,点分别为的中点,过点作交延长线于 , 连接 , 若 , 则的长为.

三、解答题(共13小题,计81分.解答应写出过程)
-
14. 解不等式:.15. 解方程:.16. 如图,在中,请用尺规作图法在上找一点 , 连接 , 使得.(保留作图痕迹,不写作法)
 17. 如图,在四边形中,连接 , 已知 , 求证:四边形是平行四边形.
17. 如图,在四边形中,连接 , 已知 , 求证:四边形是平行四边形. 18. 如图,在Rt中, , 将沿的方向平移得到 , 其中.
18. 如图,在Rt中, , 将沿的方向平移得到 , 其中.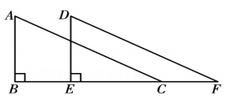 (1)、求的长;(2)、若 , 求的度数.19. 如图,在中,交于点交于点.求证:是等边三角形.
(1)、求的长;(2)、若 , 求的度数.19. 如图,在中,交于点交于点.求证:是等边三角形. 20. 解不等式组:并把解集表示在如图所示的数轴上.
20. 解不等式组:并把解集表示在如图所示的数轴上. 21. 先化简,再求值: , 其中.22. 为支援新冠肺炎疫情防控工作,提高防护服生产的效率,某工厂将使用两种型号机器生产防护服,已知型机器比型机器每小时多生产10件,且型机器生产600件所用时间与型机器生产500件所用时间相等,求这两种机器每小时分别生产多少件防护服?23. 如图,在平面直角坐标系中,的三个顶点分别是.
21. 先化简,再求值: , 其中.22. 为支援新冠肺炎疫情防控工作,提高防护服生产的效率,某工厂将使用两种型号机器生产防护服,已知型机器比型机器每小时多生产10件,且型机器生产600件所用时间与型机器生产500件所用时间相等,求这两种机器每小时分别生产多少件防护服?23. 如图,在平面直角坐标系中,的三个顶点分别是.
⑴把向左平移4个单位后得到对应的 , 点的对应点分别为、 , 请画出平移后的 , 并写出点的坐标;
⑵把绕原点旋转后得到对应的 , 点的对应点分别为、 , 请画出旋转后的 , 并写出点的坐标.
24. 阅读与思考:分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式,比如:四项的多项式一般按照“两两”分组或“三一”分组,进行分组分解.
例“两两分组”.
解:原式
例三一分组”.
解:原式
归纳总结:用分组分解法分解因式要先恰当分组,然后用提公因式法或运用公式法继续分解.请同学们在阅读材料的启发下,解答下列问题:
分解因式:
(1)、;(2)、.

